名校
解题方法
1 . 为了监控某台机器的生产过程,检验员每天从该机器生产的零件中随机抽取若干零件,并测量其尺寸(单位: ).根据长期生产经验,可以认为这台机器正常状态下生产的零件的尺寸服从正态分布
).根据长期生产经验,可以认为这台机器正常状态下生产的零件的尺寸服从正态分布 .检验员某天从生产的零件中随机抽取
.检验员某天从生产的零件中随机抽取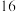 个零件,并测量其尺寸(单位:
个零件,并测量其尺寸(单位: )如下:
)如下:
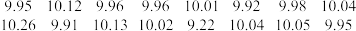
将样本的均值 作为总体均值
作为总体均值 的估计值,样本标准差
的估计值,样本标准差 作为总体标准差
作为总体标准差 的估计值.
的估计值.
根据生产经验,在一天抽检的零件中,如果出现了尺寸在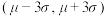 之外的零件,就认为该机器可能出现故障,需要停工检修.
之外的零件,就认为该机器可能出现故障,需要停工检修.
(1)试利用估计值判断该机器是否可能出现故障;
(2)若一台机器出现故障,则立即停工并申报维修,直到维修日都不工作.
根据长期生产经验,一台机器停工 天的总损失额
天的总损失额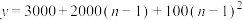 ,
, 、
、 、
、 、
、 (单位:元).现有
(单位:元).现有 种维修方案(一天完成维修)可供选择:
种维修方案(一天完成维修)可供选择:
方案一:加急维修单,维修人员会在机器出现故障的当天上门维修,维修费用为 元;
元;
方案二:常规维修单,维修人员会在机器出现故障当天或者之后 天中的任意一天上门维修,维修费用为
天中的任意一天上门维修,维修费用为 元.
元.
现统计该工厂最近 份常规维修单,获得机器在第
份常规维修单,获得机器在第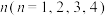 天得到维修的数据如下:
天得到维修的数据如下:
将频率视为概率,若机器出现故障,以机器维修所需费用与机器停工总损失额的和的期望值为决策依据,应选择哪种维修方案?
参考数据: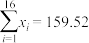 ,
,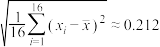 .参考公式:
.参考公式: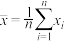 ,
, .
.
 ).根据长期生产经验,可以认为这台机器正常状态下生产的零件的尺寸服从正态分布
).根据长期生产经验,可以认为这台机器正常状态下生产的零件的尺寸服从正态分布 .检验员某天从生产的零件中随机抽取
.检验员某天从生产的零件中随机抽取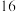 个零件,并测量其尺寸(单位:
个零件,并测量其尺寸(单位: )如下:
)如下: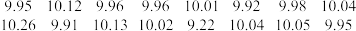
将样本的均值
 作为总体均值
作为总体均值 的估计值,样本标准差
的估计值,样本标准差 作为总体标准差
作为总体标准差 的估计值.
的估计值.根据生产经验,在一天抽检的零件中,如果出现了尺寸在
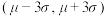 之外的零件,就认为该机器可能出现故障,需要停工检修.
之外的零件,就认为该机器可能出现故障,需要停工检修.(1)试利用估计值判断该机器是否可能出现故障;
(2)若一台机器出现故障,则立即停工并申报维修,直到维修日都不工作.
根据长期生产经验,一台机器停工
 天的总损失额
天的总损失额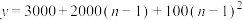 ,
, 、
、 、
、 、
、 (单位:元).现有
(单位:元).现有 种维修方案(一天完成维修)可供选择:
种维修方案(一天完成维修)可供选择:方案一:加急维修单,维修人员会在机器出现故障的当天上门维修,维修费用为
 元;
元;方案二:常规维修单,维修人员会在机器出现故障当天或者之后
 天中的任意一天上门维修,维修费用为
天中的任意一天上门维修,维修费用为 元.
元.现统计该工厂最近
 份常规维修单,获得机器在第
份常规维修单,获得机器在第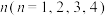 天得到维修的数据如下:
天得到维修的数据如下:
|
|
|
|
|
频数 |
|
|
|
|
参考数据:
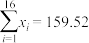 ,
, .参考公式:
.参考公式: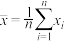 ,
, .
.
您最近一年使用:0次
2022-06-02更新
|
1128次组卷
|
4卷引用:福建省厦门集美中学2022届高三下学期适应性考试(最后一卷)数学试题
名校
解题方法
2 . 教育公平是民主社会的重要标志之一.近几年国家教育主管部门也出台了多项举措,比如“小升初”的摇号政策.某市市区有10所中学,由于历史原因,其中2所市级重点是学子心目中的一类学校,5所区重点是二类学校,另3所归为第三类.该市教育局规定:第一志愿填报一类学校,需参加摇号,如果没有摇中,则要服从分配.已知摇中的概率为 ,没有摇中,被分配到二类和三类学校的概率分别为
,没有摇中,被分配到二类和三类学校的概率分别为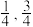 ;如果第一志愿填报二类学校,被分配到二类和三类学校的概率分别为
;如果第一志愿填报二类学校,被分配到二类和三类学校的概率分别为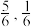 ;假设一类、二类和三类学校在学子心目中的评分分别为
;假设一类、二类和三类学校在学子心目中的评分分别为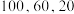 .
.
(1)分配结束后,记参加摇号学生获得的评分为 ,不参加摇号获得的评分为
,不参加摇号获得的评分为 ,以
,以 和
和 为依据说明该如何择校;
为依据说明该如何择校;
(2)招生细则中,为了方便学生就近入学,规定如果第一志愿填报二类学校,满足学校志愿的概率为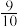 .六年级某班的3名好朋友,为了能继续在一起学习,第一志愿填报了同一所二类学校,求他们3人都能被分配到该校的概率.
.六年级某班的3名好朋友,为了能继续在一起学习,第一志愿填报了同一所二类学校,求他们3人都能被分配到该校的概率.
 ,没有摇中,被分配到二类和三类学校的概率分别为
,没有摇中,被分配到二类和三类学校的概率分别为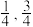 ;如果第一志愿填报二类学校,被分配到二类和三类学校的概率分别为
;如果第一志愿填报二类学校,被分配到二类和三类学校的概率分别为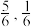 ;假设一类、二类和三类学校在学子心目中的评分分别为
;假设一类、二类和三类学校在学子心目中的评分分别为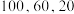 .
.(1)分配结束后,记参加摇号学生获得的评分为
 ,不参加摇号获得的评分为
,不参加摇号获得的评分为 ,以
,以 和
和 为依据说明该如何择校;
为依据说明该如何择校;(2)招生细则中,为了方便学生就近入学,规定如果第一志愿填报二类学校,满足学校志愿的概率为
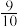 .六年级某班的3名好朋友,为了能继续在一起学习,第一志愿填报了同一所二类学校,求他们3人都能被分配到该校的概率.
.六年级某班的3名好朋友,为了能继续在一起学习,第一志愿填报了同一所二类学校,求他们3人都能被分配到该校的概率.
您最近一年使用:0次
名校
解题方法
3 . 从2021年起,全国高考数学加入了新题型多选题,每个小题给出的四个选择中有多项是正确的,其中回答错误得0分,部分正确得2分,完全正确得5分,小明根据以前做过的多项选择题统计得到,多选题有两个选项的概率为p,有三个选项的概率为 (其中
(其中 ).
).
(1)若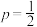 ,小明对某个多项选择题完全不会,决定随机选择一个选项,求小明得2分的概率;
,小明对某个多项选择题完全不会,决定随机选择一个选项,求小明得2分的概率;
(2)在某个多项选择题中,小明发现选项A正确,选项B错误,下面小明有三种不同策略:Ⅰ:选择A,再从剩下的C,D选项中随机选择一个,小明该题的得分为X;Ⅱ:选择ACD,小明该题的得分为Y;Ⅲ:只选择A、小明该题的得分为Z;在p变化时、根据该题得分的期望来帮助小明分析该选择哪个策略.
 (其中
(其中 ).
).(1)若
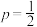 ,小明对某个多项选择题完全不会,决定随机选择一个选项,求小明得2分的概率;
,小明对某个多项选择题完全不会,决定随机选择一个选项,求小明得2分的概率;(2)在某个多项选择题中,小明发现选项A正确,选项B错误,下面小明有三种不同策略:Ⅰ:选择A,再从剩下的C,D选项中随机选择一个,小明该题的得分为X;Ⅱ:选择ACD,小明该题的得分为Y;Ⅲ:只选择A、小明该题的得分为Z;在p变化时、根据该题得分的期望来帮助小明分析该选择哪个策略.
您最近一年使用:0次
2022-05-16更新
|
767次组卷
|
3卷引用:重庆市第八中学校2022届高三下学期适应性月考(七)数学试题
解题方法
4 . 某游乐场设置了迷宫游戏,有三个造型相同的门可供选择,参与者进入三个门后结果分别是:3分钟走出去,6分钟走出去,3分钟返回出发点.游戏规定:不重复进同一个门,若返回出发点立即重新选择,走出迷宫游戏结束.
(1)求一名游戏参与者走出迷宫所用时间的期望;
(2)甲、乙2人相约玩这个游戏.2人商量了两种方案,
方案一:2人共同行动;
方案二:2人分头行动.
分别计算两种方案2人都走出迷宫所用时间和的期望.
(1)求一名游戏参与者走出迷宫所用时间的期望;
(2)甲、乙2人相约玩这个游戏.2人商量了两种方案,
方案一:2人共同行动;
方案二:2人分头行动.
分别计算两种方案2人都走出迷宫所用时间和的期望.
您最近一年使用:0次
解题方法
5 . 某游乐场开展摸球有奖活动,在一个不透明的盒子中放入大小相同的10个小球,其中红球4个,黑球6个,游客花10元钱,就可以参加一次摸球有奖活动,从盒子中一次随机摸取4个小球,规定摸取到两个或两个以上的红球就中奖.根据摸取到的红球个数,设立如下的中奖等级:
(1)求游客在一次摸球有奖活动中中奖的概率;
(2)若游乐场规定:在一次摸球有奖活动中,游客中三等奖,可获得奖金15元;中二等奖,可获得奖金20元;中一等奖,可获得奖金200元.请从游乐场获利的角度,分析此次摸球有奖活动的合理性.
摸取到的红球个数 | 2 | 3 | 4 |
中奖等级 | 三等奖 | 二等奖 | 一等奖 |
(2)若游乐场规定:在一次摸球有奖活动中,游客中三等奖,可获得奖金15元;中二等奖,可获得奖金20元;中一等奖,可获得奖金200元.请从游乐场获利的角度,分析此次摸球有奖活动的合理性.
您最近一年使用:0次
名校
6 . 在2021年5月,A市开展了庆祝中国共产党建党百年“学党史,知党情”大型党史知识竞赛活动.竞赛活动后,在参赛的人员中,随机抽取了100名参赛人员的成绩(满分150分)进行统计分析,将所抽取的100名参赛人员的成绩数据绘制成频率分布直方图如下图所示,直方图中m,n的关系为 ,根据频率分布直方图中的信息解答下列问题.
,根据频率分布直方图中的信息解答下列问题.
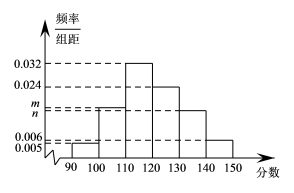
(1)从成绩在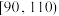 内的参赛人员中任取3人,求其中至少有2人的成绩在
内的参赛人员中任取3人,求其中至少有2人的成绩在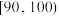 内的概率;
内的概率;
(2)用分层抽样的方法,先从成绩分别在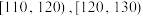 和
和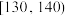 内的参赛人员中共抽取9人,再从这9人中任取4人,设抽取的4人中成绩在
内的参赛人员中共抽取9人,再从这9人中任取4人,设抽取的4人中成绩在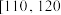 内的人数为
内的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(3)若参赛人员共有1000人,现有B公司准备拿出一定资金,奖励参赛人员中成绩在120分及以上的参赛人员,并拟订了两种奖励方案.方案一:人均奖励333元;方案二:把成绩在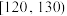 内的记为三等,成绩在
内的记为三等,成绩在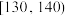 内的记为二等,成绩在
内的记为二等,成绩在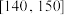 内的记为一等,并按等级每人分别奖励200元、400元和600元.若你是竞赛活动的负责人,用统计知识分析,你将选择哪一种奖励方案,并说明理由.
内的记为一等,并按等级每人分别奖励200元、400元和600元.若你是竞赛活动的负责人,用统计知识分析,你将选择哪一种奖励方案,并说明理由.
 ,根据频率分布直方图中的信息解答下列问题.
,根据频率分布直方图中的信息解答下列问题.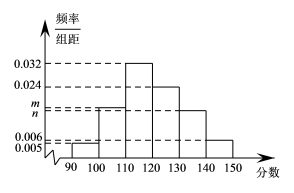
(1)从成绩在
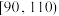 内的参赛人员中任取3人,求其中至少有2人的成绩在
内的参赛人员中任取3人,求其中至少有2人的成绩在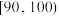 内的概率;
内的概率;(2)用分层抽样的方法,先从成绩分别在
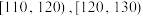 和
和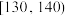 内的参赛人员中共抽取9人,再从这9人中任取4人,设抽取的4人中成绩在
内的参赛人员中共抽取9人,再从这9人中任取4人,设抽取的4人中成绩在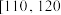 内的人数为
内的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(3)若参赛人员共有1000人,现有B公司准备拿出一定资金,奖励参赛人员中成绩在120分及以上的参赛人员,并拟订了两种奖励方案.方案一:人均奖励333元;方案二:把成绩在
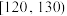 内的记为三等,成绩在
内的记为三等,成绩在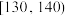 内的记为二等,成绩在
内的记为二等,成绩在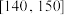 内的记为一等,并按等级每人分别奖励200元、400元和600元.若你是竞赛活动的负责人,用统计知识分析,你将选择哪一种奖励方案,并说明理由.
内的记为一等,并按等级每人分别奖励200元、400元和600元.若你是竞赛活动的负责人,用统计知识分析,你将选择哪一种奖励方案,并说明理由.
您最近一年使用:0次
2022-03-30更新
|
960次组卷
|
2卷引用:辽宁省抚顺市2022届 高三第一次模拟考试数学试题
7 . 一个袋子中有 个大小相同的球,其中有
个大小相同的球,其中有 个白球,
个白球, 个黄球,从中随机地摸
个黄球,从中随机地摸 个球作为样本,用
个球作为样本,用 表示样本中黄球的个数,
表示样本中黄球的个数, 表示样本中黄球的比例.
表示样本中黄球的比例.
(1)若有放回摸球,求 的分布列及数学期望;
的分布列及数学期望;
(2)(i)分别就有放回摸球和不放回摸球,求 与总体中黄球的比例之差的绝对值不超过
与总体中黄球的比例之差的绝对值不超过 的概率;
的概率;
(ii)比较(i)中所求概率的大小,说明其实际含义.
 个大小相同的球,其中有
个大小相同的球,其中有 个白球,
个白球, 个黄球,从中随机地摸
个黄球,从中随机地摸 个球作为样本,用
个球作为样本,用 表示样本中黄球的个数,
表示样本中黄球的个数, 表示样本中黄球的比例.
表示样本中黄球的比例.(1)若有放回摸球,求
 的分布列及数学期望;
的分布列及数学期望;(2)(i)分别就有放回摸球和不放回摸球,求
 与总体中黄球的比例之差的绝对值不超过
与总体中黄球的比例之差的绝对值不超过 的概率;
的概率;(ii)比较(i)中所求概率的大小,说明其实际含义.
您最近一年使用:0次
2021-08-06更新
|
352次组卷
|
2卷引用:湖南省长沙市雅礼中学2024届高三下学期模拟(三)数学试题
8 . 某商店为了吸引顾客,设计了两种摸球活动奖励方案.先制作一个不透明的盒子,里面放有形状大小完全相同的4个白球和2个红球.
方案一:不放回地从盒子中逐个摸球,消费金额每满300元摸一次,最终根据顾客摸到的红球个数发放奖金,如表格所示.
方案二:可放回地从盒子中逐个摸球,消费金额每满200元摸一次,每摸到一个红球奖励15元.
(1)若顾客甲消费的金额为600元,且选择了方案一,求甲获得奖金数为30元的概率;
(2)若顾客乙消费的金额为800元,但他可以在摸出第一个球后,根据所摸出球的颜色,再决定执行方案一或方案二继续摸球.请从奖金数期望最大的角度为顾客乙制定第一次摸球后的方案选择,并说明理由.
方案一:不放回地从盒子中逐个摸球,消费金额每满300元摸一次,最终根据顾客摸到的红球个数发放奖金,如表格所示.
红球个数 | 0 | 1 | 2 |
奖金 | 0元 | 30元 | 75元 |
(1)若顾客甲消费的金额为600元,且选择了方案一,求甲获得奖金数为30元的概率;
(2)若顾客乙消费的金额为800元,但他可以在摸出第一个球后,根据所摸出球的颜色,再决定执行方案一或方案二继续摸球.请从奖金数期望最大的角度为顾客乙制定第一次摸球后的方案选择,并说明理由.
您最近一年使用:0次
2021-06-03更新
|
949次组卷
|
4卷引用:重庆市第八中学2021届高三下学期模拟(八)数学试题
重庆市第八中学2021届高三下学期模拟(八)数学试题(已下线)8.7 均值与方差在生活中的运用(精练)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)河南省南阳市第一中学校2023-2024学年高三上学期开学考试数学试题湖南省常德市第二中学2020-2021学年高二(332班)下学期期末数学试题
9 . 在医学上,为了加快对流行性病毒的检测速度,常采用“混检”的方法:随机的将若干人的核酸样本混在一起进行检测,若检测结果呈阴性,则认定该组每份样本均为阴性,无需再检测;若检测结果呈阳性,则还需对该组的每份样本逐个重新检测,以确定每份样本是否为阳性.设某流行性病毒的感染率为 .
.
(1)若 ,混检时每组10人,求每组检测次数的期望值;
,混检时每组10人,求每组检测次数的期望值;
(2)混检分组的方法有两种:每组10人或30人.试问这两种分组方法的优越性与 的值是否有关?
的值是否有关?
(参考数据: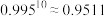 ,
,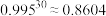 )
)
 .
.(1)若
 ,混检时每组10人,求每组检测次数的期望值;
,混检时每组10人,求每组检测次数的期望值;(2)混检分组的方法有两种:每组10人或30人.试问这两种分组方法的优越性与
 的值是否有关?
的值是否有关?(参考数据:
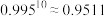 ,
,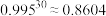 )
)
您最近一年使用:0次
解题方法
10 . 元旦期间某牛奶公司做促销活动.一箱某品牌牛奶 盒,每盒牛奶可以参与刮奖中奖得现金活动,但其中只有一些中奖.已知购买一盒牛奶需要
盒,每盒牛奶可以参与刮奖中奖得现金活动,但其中只有一些中奖.已知购买一盒牛奶需要 元,若有中奖,则每次中奖可以获得代金券
元,若有中奖,则每次中奖可以获得代金券 元(可即中即用).顾客可以在一箱牛奶中先购买
元(可即中即用).顾客可以在一箱牛奶中先购买 盒,然后根据这
盒,然后根据这 盒牛奶中奖结果决定是否购买余下
盒牛奶中奖结果决定是否购买余下 盒.设每盒牛奶中奖概率为
盒.设每盒牛奶中奖概率为 ,且每盒牛奶是否中奖相互独立.
,且每盒牛奶是否中奖相互独立.
(1)若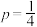 ,顾客先购买
,顾客先购买 盒牛奶,求该顾客至少有一盒中奖的概率;
盒牛奶,求该顾客至少有一盒中奖的概率;
(2)设先购买的 盒牛奶恰好有一盒中奖的最大概率为
盒牛奶恰好有一盒中奖的最大概率为 ,以
,以 为
为 值.某顾客认为如果中奖后售价不超过原来售价的四折(即
值.某顾客认为如果中奖后售价不超过原来售价的四折(即 )便可以购买如下的
)便可以购买如下的 盒牛奶,据此,请你判断该顾客是否可以购买余下的
盒牛奶,据此,请你判断该顾客是否可以购买余下的 盒牛奶.
盒牛奶.
 盒,每盒牛奶可以参与刮奖中奖得现金活动,但其中只有一些中奖.已知购买一盒牛奶需要
盒,每盒牛奶可以参与刮奖中奖得现金活动,但其中只有一些中奖.已知购买一盒牛奶需要 元,若有中奖,则每次中奖可以获得代金券
元,若有中奖,则每次中奖可以获得代金券 元(可即中即用).顾客可以在一箱牛奶中先购买
元(可即中即用).顾客可以在一箱牛奶中先购买 盒,然后根据这
盒,然后根据这 盒牛奶中奖结果决定是否购买余下
盒牛奶中奖结果决定是否购买余下 盒.设每盒牛奶中奖概率为
盒.设每盒牛奶中奖概率为 ,且每盒牛奶是否中奖相互独立.
,且每盒牛奶是否中奖相互独立.(1)若
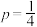 ,顾客先购买
,顾客先购买 盒牛奶,求该顾客至少有一盒中奖的概率;
盒牛奶,求该顾客至少有一盒中奖的概率;(2)设先购买的
 盒牛奶恰好有一盒中奖的最大概率为
盒牛奶恰好有一盒中奖的最大概率为 ,以
,以 为
为 值.某顾客认为如果中奖后售价不超过原来售价的四折(即
值.某顾客认为如果中奖后售价不超过原来售价的四折(即 )便可以购买如下的
)便可以购买如下的 盒牛奶,据此,请你判断该顾客是否可以购买余下的
盒牛奶,据此,请你判断该顾客是否可以购买余下的 盒牛奶.
盒牛奶.
您最近一年使用:0次






