1 . 已知函数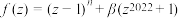 ,其中
,其中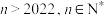 ,证明:存在
,证明:存在 ,且
,且 .
.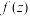 的根的实部全部大于0.
的根的实部全部大于0.
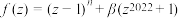 ,其中
,其中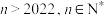 ,证明:存在
,证明:存在 ,且
,且 .
.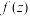 的根的实部全部大于0.
的根的实部全部大于0.
您最近一年使用:0次
名校
2 . 利用平面向量的坐标表示,可以把平面向量的概念推广为坐标为复数的“复向量”,即可将有序复数对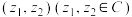 视为一个向量,记作
视为一个向量,记作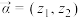 .类比平面向量可以定义其运算,两个复向量
.类比平面向量可以定义其运算,两个复向量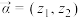 ,
,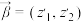 的数量积定义为一个复数,记作
的数量积定义为一个复数,记作 ,满足
,满足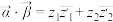 ,复向量
,复向量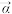 的模定义为
的模定义为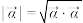 .
.
(1)设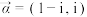 ,
,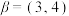 ,求复向量
,求复向量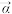 ,
,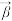 的模;
的模;
(2)设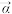 、
、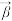 是两个复向量,证明柯西一布涅科夫斯基不等式仍成立,即:
是两个复向量,证明柯西一布涅科夫斯基不等式仍成立,即: ;
;
(3)当 时,称复向量
时,称复向量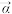 与
与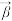 平行.设
平行.设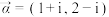 、
、 ,若复向量
,若复向量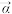 与
与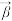 平行,求复数
平行,求复数 的值.
的值.
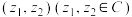 视为一个向量,记作
视为一个向量,记作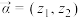 .类比平面向量可以定义其运算,两个复向量
.类比平面向量可以定义其运算,两个复向量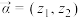 ,
,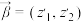 的数量积定义为一个复数,记作
的数量积定义为一个复数,记作 ,满足
,满足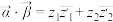 ,复向量
,复向量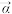 的模定义为
的模定义为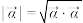 .
.(1)设
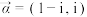 ,
,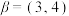 ,求复向量
,求复向量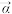 ,
,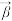 的模;
的模;(2)设
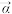 、
、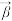 是两个复向量,证明柯西一布涅科夫斯基不等式仍成立,即:
是两个复向量,证明柯西一布涅科夫斯基不等式仍成立,即: ;
;(3)当
 时,称复向量
时,称复向量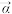 与
与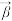 平行.设
平行.设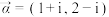 、
、 ,若复向量
,若复向量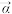 与
与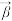 平行,求复数
平行,求复数 的值.
的值.
您最近一年使用:0次
2021-07-12更新
|
1279次组卷
|
9卷引用:专题05 复数压轴题型汇总-2021-2022学年高一《新题速递·数学》(人教A版2019)
(已下线)专题05 复数压轴题型汇总-2021-2022学年高一《新题速递·数学》(人教A版2019)(已下线)第02讲 复数的运算-【帮课堂】2021-2022学年高一数学同步精品讲义(苏教版2019必修第二册)上海交通大学附属中学2020-2021学年高一下学期期末数学试题(已下线)7.2复数的四则运算C卷第12章 复数(单元测试)-2022-2023学年高一数学同步精品课堂(苏教版2019必修第二册)高一复数重难点提高卷-【同步题型讲义】(已下线)第七章 复数(基础、典型、易错、压轴)分类专项训练(2)(已下线)复数的概念与运算(已下线)第7章 复数-《重难点题型·高分突破》(人教A版2019必修第二册)
3 . 求证:
(1)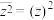 ;
;
(2) ;
;
(3)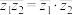 ;
;
(4)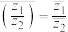 .
.
(1)
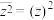 ;
;(2)
 ;
;(3)
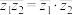 ;
;(4)
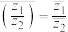 .
.
您最近一年使用:0次
2020-01-30更新
|
1273次组卷
|
6卷引用:专题05 复数压轴题型汇总-2021-2022学年高一《新题速递·数学》(人教A版2019)
(已下线)专题05 复数压轴题型汇总-2021-2022学年高一《新题速递·数学》(人教A版2019)人教B版(2019) 必修第四册 逆袭之路 第十章 10.2.2 复数的乘法与除法(已下线)第19讲压轴综合题(讲义)-【教育机构专用】2021年春季高一数学辅导讲义(沪教版2020必修第二册)(已下线)第十章 复数 10.2 复数的运算 10.2.2 复数的乘法与除法人教B版(2019)必修第四册课本习题10.2.2 复数的乘法与除法(已下线)第七章 复数(基础、典型、易错、压轴)分类专项训练(2)
名校
4 . 设复平面上点 对应的复数
对应的复数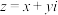
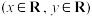 (
( 为虚数单位)满足
为虚数单位)满足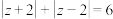 ,点
,点 的轨迹方程为曲线
的轨迹方程为曲线 . 双曲线
. 双曲线 :
: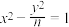 与曲线
与曲线 有共同焦点,倾斜角为
有共同焦点,倾斜角为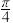 的直线
的直线 与双曲线
与双曲线 的两条渐近线的交点是
的两条渐近线的交点是 、
、 ,
,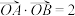 ,
, 为坐标原点.
为坐标原点.
(1)求点 的轨迹方程
的轨迹方程 ;
;
(2)求直线 的方程;
的方程;
(3)设△PQR三个顶点在曲线 上,求证:当
上,求证:当 是△PQR重心时,△PQR的面积是定值.
是△PQR重心时,△PQR的面积是定值.
 对应的复数
对应的复数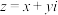
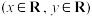 (
( 为虚数单位)满足
为虚数单位)满足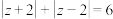 ,点
,点 的轨迹方程为曲线
的轨迹方程为曲线 . 双曲线
. 双曲线 :
: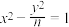 与曲线
与曲线 有共同焦点,倾斜角为
有共同焦点,倾斜角为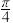 的直线
的直线 与双曲线
与双曲线 的两条渐近线的交点是
的两条渐近线的交点是 、
、 ,
,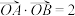 ,
, 为坐标原点.
为坐标原点. (1)求点
 的轨迹方程
的轨迹方程 ;
;(2)求直线
 的方程;
的方程;(3)设△PQR三个顶点在曲线
 上,求证:当
上,求证:当 是△PQR重心时,△PQR的面积是定值.
是△PQR重心时,△PQR的面积是定值.
您最近一年使用:0次
2018-04-16更新
|
1085次组卷
|
4卷引用:考向30 复数-备战2022年高考数学一轮复习考点微专题(上海专用)
(已下线)考向30 复数-备战2022年高考数学一轮复习考点微专题(上海专用)上海实验学校2022届高三冲刺模拟卷二数学试题上海市奉贤区2018届高三下学期调研测试(二模)数学试题上海市位育中学2021届高三下学期开学考试数学试题
5 . 已知 是虚数,
是虚数,  是实数.
是实数.
(1)求 为何值时,
为何值时, 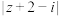 有最小值,并求出|
有最小值,并求出|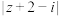 的最小值;
的最小值;
(2)设 ,求证:
,求证:  为纯虚数.
为纯虚数.
 是虚数,
是虚数,  是实数.
是实数.(1)求
 为何值时,
为何值时, 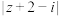 有最小值,并求出|
有最小值,并求出|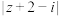 的最小值;
的最小值;(2)设
 ,求证:
,求证:  为纯虚数.
为纯虚数.
您最近一年使用:0次
2017-05-21更新
|
2187次组卷
|
4卷引用:专题16 复数——常见中档题型汇编-【重难点突破】2021-2022学年高一数学常考题专练(人教A版2019必修第二册)
(已下线)专题16 复数——常见中档题型汇编-【重难点突破】2021-2022学年高一数学常考题专练(人教A版2019必修第二册)江苏省江阴市四校2016-2017学年高二下学期期中考试数学(理)试题安徽省定远重点中学2017-2018学年高二下学期教学段考数学(理)试题江苏省苏州市吴中区2018-2019学年高二下学期期中数学(理)试题



