1 . 已知双曲线 的右焦点为
的右焦点为 ,双曲线
,双曲线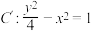 的上焦点为
的上焦点为 ,直线
,直线 ,且
,且 既是
既是 的渐近线也是
的渐近线也是 的渐近线.
的渐近线.
(1)求 的方程;
的方程;
(2)过 作与
作与 轴不垂直的直线与
轴不垂直的直线与 的右支交于点
的右支交于点 ,若点
,若点 在
在 轴上,且
轴上,且 ,求证:
,求证: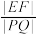 为定值,并求出该定值.
为定值,并求出该定值.
 的右焦点为
的右焦点为 ,双曲线
,双曲线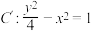 的上焦点为
的上焦点为 ,直线
,直线 ,且
,且 既是
既是 的渐近线也是
的渐近线也是 的渐近线.
的渐近线.(1)求
 的方程;
的方程;(2)过
 作与
作与 轴不垂直的直线与
轴不垂直的直线与 的右支交于点
的右支交于点 ,若点
,若点 在
在 轴上,且
轴上,且 ,求证:
,求证: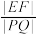 为定值,并求出该定值.
为定值,并求出该定值.
您最近一年使用:0次
2 . 已知双曲线 过点
过点 ,左、右顶点分别为
,左、右顶点分别为 ,
, ,直线
,直线 与直线
与直线 的斜率之和为
的斜率之和为 .
.
(1)求双曲线的标准方程;
(2)过双曲线右焦点 的直线
的直线 交双曲线右支于
交双曲线右支于 ,
, (
( 在第一象限)两点,
在第一象限)两点,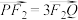 ,
, 是双曲线上一点,
是双曲线上一点,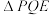 的重心在
的重心在 轴上,求点
轴上,求点 的坐标.
的坐标.
 过点
过点 ,左、右顶点分别为
,左、右顶点分别为 ,
, ,直线
,直线 与直线
与直线 的斜率之和为
的斜率之和为 .
.(1)求双曲线的标准方程;
(2)过双曲线右焦点
 的直线
的直线 交双曲线右支于
交双曲线右支于 ,
, (
( 在第一象限)两点,
在第一象限)两点,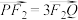 ,
, 是双曲线上一点,
是双曲线上一点,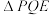 的重心在
的重心在 轴上,求点
轴上,求点 的坐标.
的坐标.
您最近一年使用:0次
7日内更新
|
90次组卷
|
2卷引用:贵州省六盘水市盘州市第一中学2023-2024学年高二下学期期末考试数学试题
2024高三·全国·专题练习
解题方法
3 . 在平面直角坐标系中,双曲线 的中心在原点,它的一个焦点坐标为
的中心在原点,它的一个焦点坐标为 ,
,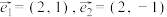 分别是两条渐近线的方向向量.任取双曲线
分别是两条渐近线的方向向量.任取双曲线 上的点
上的点 ,若
,若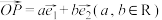 ,求证:
,求证: 为定值.
为定值.
 的中心在原点,它的一个焦点坐标为
的中心在原点,它的一个焦点坐标为 ,
,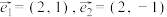 分别是两条渐近线的方向向量.任取双曲线
分别是两条渐近线的方向向量.任取双曲线 上的点
上的点 ,若
,若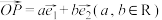 ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
4 . 已知 是双曲线
是双曲线 的左右焦点,
的左右焦点, ,点
,点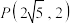 在双曲线上.
在双曲线上.
(1)求双曲线的标准方程;
(2)若直线 与双曲线相切与于点
与双曲线相切与于点 ,与双曲线的两条渐近线分别相交于
,与双曲线的两条渐近线分别相交于 两点,当点
两点,当点 在双曲线上运动时,
在双曲线上运动时,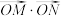 的值是否为定值?若是,求出定值;否则,请说明理由.
的值是否为定值?若是,求出定值;否则,请说明理由.
 是双曲线
是双曲线 的左右焦点,
的左右焦点, ,点
,点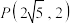 在双曲线上.
在双曲线上.(1)求双曲线的标准方程;
(2)若直线
 与双曲线相切与于点
与双曲线相切与于点 ,与双曲线的两条渐近线分别相交于
,与双曲线的两条渐近线分别相交于 两点,当点
两点,当点 在双曲线上运动时,
在双曲线上运动时,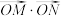 的值是否为定值?若是,求出定值;否则,请说明理由.
的值是否为定值?若是,求出定值;否则,请说明理由.
您最近一年使用:0次
解题方法
5 . 已知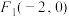 ,
,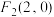 ,
, 是圆
是圆 上任意一点,点
上任意一点,点 关于点
关于点 的对称点为
的对称点为 ,线段
,线段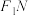 的中垂线与直线
的中垂线与直线 相交于点
相交于点 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)过点 且斜率为
且斜率为 的直线
的直线 交曲线
交曲线 位于
位于 轴右侧的部分于不同的A,B两点,
轴右侧的部分于不同的A,B两点, 为
为 轴上一点且满足
轴上一点且满足 ,试探究
,试探究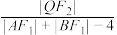 是否为定值,若是,则求出该定值;若不是,请说明理由.
是否为定值,若是,则求出该定值;若不是,请说明理由.
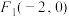 ,
,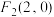 ,
, 是圆
是圆 上任意一点,点
上任意一点,点 关于点
关于点 的对称点为
的对称点为 ,线段
,线段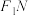 的中垂线与直线
的中垂线与直线 相交于点
相交于点 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)过点
 且斜率为
且斜率为 的直线
的直线 交曲线
交曲线 位于
位于 轴右侧的部分于不同的A,B两点,
轴右侧的部分于不同的A,B两点, 为
为 轴上一点且满足
轴上一点且满足 ,试探究
,试探究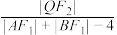 是否为定值,若是,则求出该定值;若不是,请说明理由.
是否为定值,若是,则求出该定值;若不是,请说明理由.
您最近一年使用:0次
名校
解题方法
6 . 已知双曲线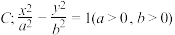 经过点
经过点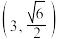 ,右焦点为
,右焦点为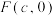 ,且
,且 成等差数列.
成等差数列.
(1)求 的方程;
的方程;
(2)过 的直线与
的直线与 的右支交于
的右支交于 两点(
两点( 在
在 的上方),
的上方), 的中点为
的中点为 在直线
在直线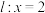 上的射影为
上的射影为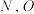 为坐标原点,设
为坐标原点,设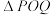 的面积为
的面积为 ,直线
,直线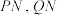 的斜率分别为
的斜率分别为 ,试问
,试问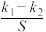 是否为定值,如果是,求出该定值,如果不是,说明理由.
是否为定值,如果是,求出该定值,如果不是,说明理由.
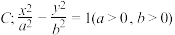 经过点
经过点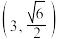 ,右焦点为
,右焦点为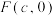 ,且
,且 成等差数列.
成等差数列.(1)求
 的方程;
的方程;(2)过
 的直线与
的直线与 的右支交于
的右支交于 两点(
两点( 在
在 的上方),
的上方), 的中点为
的中点为 在直线
在直线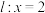 上的射影为
上的射影为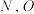 为坐标原点,设
为坐标原点,设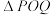 的面积为
的面积为 ,直线
,直线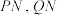 的斜率分别为
的斜率分别为 ,试问
,试问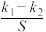 是否为定值,如果是,求出该定值,如果不是,说明理由.
是否为定值,如果是,求出该定值,如果不是,说明理由.
您最近一年使用:0次
2024-07-20更新
|
202次组卷
|
3卷引用:陕西省西安市工业大学附属中2023-2024学年高二下学期期中考试数学试题
陕西省西安市工业大学附属中2023-2024学年高二下学期期中考试数学试题河南省鹤壁市高中2023-2024学年高二下学期7月期末考试数学试题(已下线)专题13 圆锥曲线中的齐次化(高三压轴题)【练】
7 . 已知双曲线 的实轴长是虚轴长的
的实轴长是虚轴长的 倍,且焦点到渐近线的距离为
倍,且焦点到渐近线的距离为 .
.
(1)求双曲线 的方程;
的方程;
(2)若动直线 与双曲线
与双曲线 恰有1个公共点,且与双曲线
恰有1个公共点,且与双曲线 的两条渐近线交于
的两条渐近线交于 ,
, 两点,
两点, 为坐标原点,证明:
为坐标原点,证明: 的面积为定值.
的面积为定值.
 的实轴长是虚轴长的
的实轴长是虚轴长的 倍,且焦点到渐近线的距离为
倍,且焦点到渐近线的距离为 .
.(1)求双曲线
 的方程;
的方程;(2)若动直线
 与双曲线
与双曲线 恰有1个公共点,且与双曲线
恰有1个公共点,且与双曲线 的两条渐近线交于
的两条渐近线交于 ,
, 两点,
两点, 为坐标原点,证明:
为坐标原点,证明: 的面积为定值.
的面积为定值.
您最近一年使用:0次
2024-07-20更新
|
424次组卷
|
3卷引用:甘肃省2023-2024学年高二下学期教学质量统一检测数学试题
8 . 已知双曲线 的实轴长为2,离心率为2,右焦点为
的实轴长为2,离心率为2,右焦点为 ,
, 为
为 上的一个动点,
上的一个动点,
(1)若点 在双曲线
在双曲线 右支上,在
右支上,在 轴的负半轴上是否存在定点
轴的负半轴上是否存在定点 .使得
.使得 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(2)过 作圆
作圆 的两条切线
的两条切线 ,若切线
,若切线 分别与
分别与 相交于另外的两点
相交于另外的两点 、
、 ,证明:
,证明: 三点共线.
三点共线.
 的实轴长为2,离心率为2,右焦点为
的实轴长为2,离心率为2,右焦点为 ,
, 为
为 上的一个动点,
上的一个动点,(1)若点
 在双曲线
在双曲线 右支上,在
右支上,在 轴的负半轴上是否存在定点
轴的负半轴上是否存在定点 .使得
.使得 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(2)过
 作圆
作圆 的两条切线
的两条切线 ,若切线
,若切线 分别与
分别与 相交于另外的两点
相交于另外的两点 、
、 ,证明:
,证明: 三点共线.
三点共线.
您最近一年使用:0次
解题方法
9 . 已知双曲线 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 是直线
是直线 :
: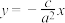 (其中
(其中 是实半轴长,
是实半轴长, 是半焦距)上不同于原点
是半焦距)上不同于原点 的一个动点,斜率为
的一个动点,斜率为 的直线
的直线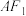 与双曲线
与双曲线 交于
交于 ,
, 两点,斜率为
两点,斜率为 的直线
的直线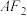 与双曲线
与双曲线 交于
交于 ,
, 两点.
两点.
(1)求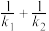 的值;
的值;
(2)若直线 ,
, ,
, ,
,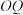 的斜率分别为
的斜率分别为 ,
, ,
,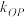 ,
,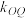 ,问是否存在点
,问是否存在点 ,满足
,满足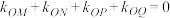 ,若存在,求出
,若存在,求出 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 是直线
是直线 :
: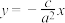 (其中
(其中 是实半轴长,
是实半轴长, 是半焦距)上不同于原点
是半焦距)上不同于原点 的一个动点,斜率为
的一个动点,斜率为 的直线
的直线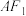 与双曲线
与双曲线 交于
交于 ,
, 两点,斜率为
两点,斜率为 的直线
的直线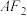 与双曲线
与双曲线 交于
交于 ,
, 两点.
两点.(1)求
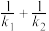 的值;
的值;(2)若直线
 ,
, ,
, ,
,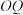 的斜率分别为
的斜率分别为 ,
, ,
,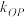 ,
,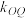 ,问是否存在点
,问是否存在点 ,满足
,满足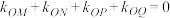 ,若存在,求出
,若存在,求出 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
您最近一年使用:0次
10 . 已知 为平面上一个动点,
为平面上一个动点, 到定直线
到定直线 的距离与到定点
的距离与到定点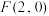 距离的比等于
距离的比等于 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)过点 的直线
的直线 与曲线
与曲线 交于
交于 ,
, 两点,在
两点,在 轴上是否存在点
轴上是否存在点 ,使得
,使得 为定值?若存在,求出该定值;若不存在,请说明理由.
为定值?若存在,求出该定值;若不存在,请说明理由.
 为平面上一个动点,
为平面上一个动点, 到定直线
到定直线 的距离与到定点
的距离与到定点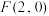 距离的比等于
距离的比等于 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)过点
 的直线
的直线 与曲线
与曲线 交于
交于 ,
, 两点,在
两点,在 轴上是否存在点
轴上是否存在点 ,使得
,使得 为定值?若存在,求出该定值;若不存在,请说明理由.
为定值?若存在,求出该定值;若不存在,请说明理由.
您最近一年使用:0次



