解题方法
1 . 已知双曲线 经过点
经过点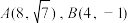 .
.
(1)求 的离心率;
的离心率;
(2)设直线 经过
经过 的右焦点,且与
的右焦点,且与 交于不同的两点
交于不同的两点 ,点N关于x轴的对称点为点P,证明:直线
,点N关于x轴的对称点为点P,证明:直线 过定点.
过定点.
 经过点
经过点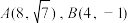 .
.(1)求
 的离心率;
的离心率;(2)设直线
 经过
经过 的右焦点,且与
的右焦点,且与 交于不同的两点
交于不同的两点 ,点N关于x轴的对称点为点P,证明:直线
,点N关于x轴的对称点为点P,证明:直线 过定点.
过定点.
您最近一年使用:0次
2 . 已知双曲线 过点
过点 ,左、右顶点分别为
,左、右顶点分别为 ,
, ,直线
,直线 与直线
与直线 的斜率之和为
的斜率之和为 .
.
(1)求双曲线的标准方程;
(2)过双曲线右焦点 的直线
的直线 交双曲线右支于
交双曲线右支于 ,
, (
( 在第一象限)两点,
在第一象限)两点,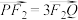 ,
, 是双曲线上一点,
是双曲线上一点,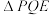 的重心在
的重心在 轴上,求点
轴上,求点 的坐标.
的坐标.
 过点
过点 ,左、右顶点分别为
,左、右顶点分别为 ,
, ,直线
,直线 与直线
与直线 的斜率之和为
的斜率之和为 .
.(1)求双曲线的标准方程;
(2)过双曲线右焦点
 的直线
的直线 交双曲线右支于
交双曲线右支于 ,
, (
( 在第一象限)两点,
在第一象限)两点,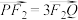 ,
, 是双曲线上一点,
是双曲线上一点,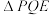 的重心在
的重心在 轴上,求点
轴上,求点 的坐标.
的坐标.
您最近一年使用:0次
7日内更新
|
90次组卷
|
2卷引用:贵州省六盘水市盘州市第一中学2023-2024学年高二下学期期末考试数学试题
解题方法
3 . 已知双曲线 :
: (
( ,
, )经过点
)经过点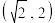 ,且其离心率为
,且其离心率为 .
.
(1)求双曲线 的方程;
的方程;
(2)设双曲线 的左,右焦点分别为
的左,右焦点分别为 ,
, ,
, 的一条渐近线上有一点
的一条渐近线上有一点 ,满足
,满足 恰好垂直于这条渐近线,求
恰好垂直于这条渐近线,求 的面积.
的面积.
 :
: (
( ,
, )经过点
)经过点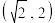 ,且其离心率为
,且其离心率为 .
.(1)求双曲线
 的方程;
的方程;(2)设双曲线
 的左,右焦点分别为
的左,右焦点分别为 ,
, ,
, 的一条渐近线上有一点
的一条渐近线上有一点 ,满足
,满足 恰好垂直于这条渐近线,求
恰好垂直于这条渐近线,求 的面积.
的面积.
您最近一年使用:0次
解题方法
4 . 已知点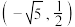 ,
,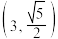 在双曲线
在双曲线 (
( ,
, )上,直线
)上,直线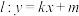 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)当 且
且 时,直线
时,直线 与双曲线
与双曲线 分别交于
分别交于 ,
, 两点,
两点, 关于
关于 轴的对称点为
轴的对称点为 .证明:直线
.证明:直线 过定点;
过定点;
(3)当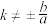 时,直线
时,直线 与双曲线
与双曲线 有唯一的公共点
有唯一的公共点 ,过点
,过点 且与
且与 垂直的直线分别交
垂直的直线分别交 轴,
轴, 轴于
轴于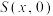 ,
,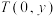 两点.当点
两点.当点 运动时,求点
运动时,求点 的轨迹方程.
的轨迹方程.
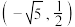 ,
,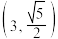 在双曲线
在双曲线 (
( ,
, )上,直线
)上,直线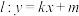 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)当
 且
且 时,直线
时,直线 与双曲线
与双曲线 分别交于
分别交于 ,
, 两点,
两点, 关于
关于 轴的对称点为
轴的对称点为 .证明:直线
.证明:直线 过定点;
过定点;(3)当
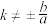 时,直线
时,直线 与双曲线
与双曲线 有唯一的公共点
有唯一的公共点 ,过点
,过点 且与
且与 垂直的直线分别交
垂直的直线分别交 轴,
轴, 轴于
轴于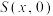 ,
,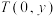 两点.当点
两点.当点 运动时,求点
运动时,求点 的轨迹方程.
的轨迹方程.
您最近一年使用:0次
7日内更新
|
75次组卷
|
2卷引用:云南省红河州文山州2023-2024学年高二下学期末学业质量监测数学试题
2024高三·全国·专题练习
解题方法
5 . 已知双曲线 的离心率为
的离心率为 ,且经过点
,且经过点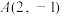 .点M,N在y轴上,
.点M,N在y轴上,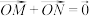 (O为坐标原点),直线AM,AN分别交双曲线C于P,Q两点.
(O为坐标原点),直线AM,AN分别交双曲线C于P,Q两点.
(1)求双曲线C的方程.
(2)求点O到直线PQ的距离的最大值.
 的离心率为
的离心率为 ,且经过点
,且经过点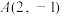 .点M,N在y轴上,
.点M,N在y轴上,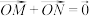 (O为坐标原点),直线AM,AN分别交双曲线C于P,Q两点.
(O为坐标原点),直线AM,AN分别交双曲线C于P,Q两点.(1)求双曲线C的方程.
(2)求点O到直线PQ的距离的最大值.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
6 . 直线 与双曲线
与双曲线
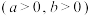 相交于
相交于 ,
, 两点,若以
两点,若以 为直径的圆过原点,且双曲线的离心率为
为直径的圆过原点,且双曲线的离心率为 ,求双曲线的方程.
,求双曲线的方程.
 与双曲线
与双曲线
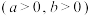 相交于
相交于 ,
, 两点,若以
两点,若以 为直径的圆过原点,且双曲线的离心率为
为直径的圆过原点,且双曲线的离心率为 ,求双曲线的方程.
,求双曲线的方程.
您最近一年使用:0次
2024高三·全国·专题练习
7 . 已知等轴双曲线 的两个焦点
的两个焦点 、
、 在直线
在直线 上,线段
上,线段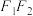 的中点是坐标原点,且双曲线经过点
的中点是坐标原点,且双曲线经过点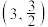 .
. 的方程:①
的方程:① ;②
;② ;③
;③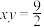 .请确定哪个是等轴双曲线
.请确定哪个是等轴双曲线 的方程,并求出此双曲线的实轴长;
的方程,并求出此双曲线的实轴长;
(2)现要在等轴双曲线 上选一处
上选一处 建一座码头,向
建一座码头,向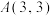 、
、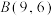 两地转运货物.经测算,从
两地转运货物.经测算,从 到
到 、从
、从 到
到 修建公路的费用都是每单位长度
修建公路的费用都是每单位长度 万元,则码头应建在何处,才能使修建两条公路的总费用最低?
万元,则码头应建在何处,才能使修建两条公路的总费用最低?
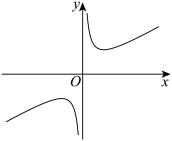
(3)如图,函数 的图像也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
的图像也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
 的两个焦点
的两个焦点 、
、 在直线
在直线 上,线段
上,线段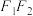 的中点是坐标原点,且双曲线经过点
的中点是坐标原点,且双曲线经过点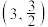 .
.
 的方程:①
的方程:① ;②
;② ;③
;③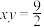 .请确定哪个是等轴双曲线
.请确定哪个是等轴双曲线 的方程,并求出此双曲线的实轴长;
的方程,并求出此双曲线的实轴长;(2)现要在等轴双曲线
 上选一处
上选一处 建一座码头,向
建一座码头,向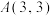 、
、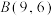 两地转运货物.经测算,从
两地转运货物.经测算,从 到
到 、从
、从 到
到 修建公路的费用都是每单位长度
修建公路的费用都是每单位长度 万元,则码头应建在何处,才能使修建两条公路的总费用最低?
万元,则码头应建在何处,才能使修建两条公路的总费用最低?(3)如图,函数
 的图像也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
的图像也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
您最近一年使用:0次
名校
解题方法
8 . 已知双曲线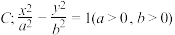 经过点
经过点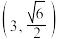 ,右焦点为
,右焦点为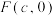 ,且
,且 成等差数列.
成等差数列.
(1)求 的方程;
的方程;
(2)过 的直线与
的直线与 的右支交于
的右支交于 两点(
两点( 在
在 的上方),
的上方), 的中点为
的中点为 在直线
在直线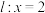 上的射影为
上的射影为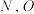 为坐标原点,设
为坐标原点,设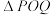 的面积为
的面积为 ,直线
,直线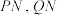 的斜率分别为
的斜率分别为 ,试问
,试问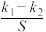 是否为定值,如果是,求出该定值,如果不是,说明理由.
是否为定值,如果是,求出该定值,如果不是,说明理由.
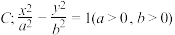 经过点
经过点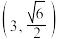 ,右焦点为
,右焦点为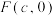 ,且
,且 成等差数列.
成等差数列.(1)求
 的方程;
的方程;(2)过
 的直线与
的直线与 的右支交于
的右支交于 两点(
两点( 在
在 的上方),
的上方), 的中点为
的中点为 在直线
在直线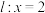 上的射影为
上的射影为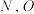 为坐标原点,设
为坐标原点,设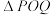 的面积为
的面积为 ,直线
,直线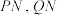 的斜率分别为
的斜率分别为 ,试问
,试问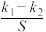 是否为定值,如果是,求出该定值,如果不是,说明理由.
是否为定值,如果是,求出该定值,如果不是,说明理由.
您最近一年使用:0次
2024-07-20更新
|
202次组卷
|
3卷引用:陕西省西安市工业大学附属中2023-2024学年高二下学期期中考试数学试题
陕西省西安市工业大学附属中2023-2024学年高二下学期期中考试数学试题河南省鹤壁市高中2023-2024学年高二下学期7月期末考试数学试题(已下线)专题13 圆锥曲线中的齐次化(高三压轴题)【练】
9 . 以椭圆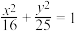 的焦点为顶点,且过点
的焦点为顶点,且过点 的双曲线标准方程是
的双曲线标准方程是______ .
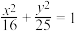 的焦点为顶点,且过点
的焦点为顶点,且过点 的双曲线标准方程是
的双曲线标准方程是
您最近一年使用:0次
解题方法
10 . 与椭圆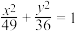 有公共焦点,且过点
有公共焦点,且过点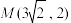 的双曲线方程为
的双曲线方程为______ .
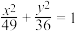 有公共焦点,且过点
有公共焦点,且过点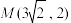 的双曲线方程为
的双曲线方程为
您最近一年使用:0次



