1 . 固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程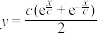 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数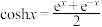 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数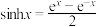 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.
(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论: _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);
(2)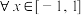 ,不等式
,不等式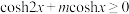 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若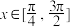 ,试比较
,试比较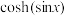 与
与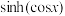 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
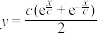 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数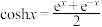 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数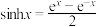 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论:
 _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);(2)
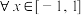 ,不等式
,不等式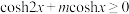 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
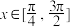 ,试比较
,试比较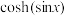 与
与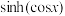 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
您最近一年使用:0次
2024-01-27更新
|
1513次组卷
|
14卷引用:重庆市缙云教育联盟2024届高三下学期2月月度质量检测数学试题
重庆市缙云教育联盟2024届高三下学期2月月度质量检测数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)讲(已下线)拔高点突破05 函数与导数背景下的新定义压轴解答题(九大题型)(已下线)拔高点突破01 三角函数与解三角形背景下的新定义问题(十大题型)(已下线)专题2 函数与导数新定义压轴大题(一)【讲】福建省宁德市2023-2024学年高一上学期1月期末质量检测数学试题河南省名校联盟2023-2024学年高一下学期3月测试数学试题(已下线)第八章:向量的数量积与三角恒等变换章末重点题型复习(2)-同步精品课堂(人教B版2019必修第三册)河南省信阳市信阳高级中学2023-2024学年高一下学期3月月考(一)数学试题(已下线)第8章:向量的数量积与三角恒等变换章末综合检测卷(新题型)-【帮课堂】(人教B版2019必修第三册)(已下线)专题04 三角函数恒等变形综合大题归类 -期末考点大串讲(苏教版(2019))(已下线)专题08 期末必刷解答题专题训练的7种常考题型归类-期末真题分类汇编(北师大版2019必修第二册)江西省上饶市横峰县横峰中学2023-2024学年高一下学期期中考试数学试卷云南省昆明市云南师范大学附属中学2023-2024学年高一下学期期末数学模拟测试试题(一)
名校
解题方法
2 . 设函数 定义在区间
定义在区间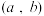 上,若对任意的
上,若对任意的 、
、 、
、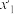 、
、
 ,当
,当 ,且
,且 时,不等式
时,不等式 成立,就称函数
成立,就称函数 具有M性质.
具有M性质.
(1)判断函数 ,
,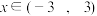 是否具有M性质,并说明理由;
是否具有M性质,并说明理由;
(2)已知函数 在区间
在区间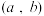 上恒正,且函数
上恒正,且函数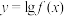 ,
,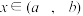 具有M性质,求证:对任意的
具有M性质,求证:对任意的 、
、
 ,且
,且 ,有
,有 ;
;
(3)①已知函数 ,
,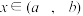 具有M性质,证明:对任意的
具有M性质,证明:对任意的 、
、 、
、
 ,有
,有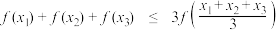 ,其中等号当且仅当
,其中等号当且仅当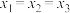 时成立;
时成立;
②已知函数 ,
,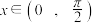 具有M性质,若
具有M性质,若 、
、 、
、 为三角形
为三角形 的内角,求
的内角,求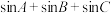 的最大值.
的最大值.
(可参考:对于任意给定实数 、
、 ,有
,有 ,且等号当且仅当
,且等号当且仅当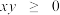 时成立.)
时成立.)
 定义在区间
定义在区间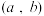 上,若对任意的
上,若对任意的 、
、 、
、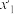 、
、
 ,当
,当 ,且
,且 时,不等式
时,不等式 成立,就称函数
成立,就称函数 具有M性质.
具有M性质.(1)判断函数
 ,
,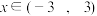 是否具有M性质,并说明理由;
是否具有M性质,并说明理由;(2)已知函数
 在区间
在区间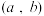 上恒正,且函数
上恒正,且函数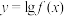 ,
,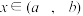 具有M性质,求证:对任意的
具有M性质,求证:对任意的 、
、
 ,且
,且 ,有
,有 ;
;(3)①已知函数
 ,
,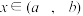 具有M性质,证明:对任意的
具有M性质,证明:对任意的 、
、 、
、
 ,有
,有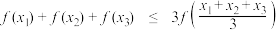 ,其中等号当且仅当
,其中等号当且仅当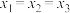 时成立;
时成立;②已知函数
 ,
,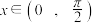 具有M性质,若
具有M性质,若 、
、 、
、 为三角形
为三角形 的内角,求
的内角,求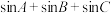 的最大值.
的最大值.(可参考:对于任意给定实数
 、
、 ,有
,有 ,且等号当且仅当
,且等号当且仅当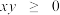 时成立.)
时成立.)
您最近一年使用:0次
2021-12-27更新
|
777次组卷
|
5卷引用:上海市黄浦区2022届高三一模数学试题
上海市黄浦区2022届高三一模数学试题(已下线)上海市黄浦区2022届高三上学期一模数学试题(已下线)第04讲 函数最值与性质-3上海市文来高中2023届高三上学期期中数学试题(已下线)专题06 期末解答压轴题-《期末真题分类汇编》(上海专用)
3 . 在平面直角坐标系 中,利用公式
中,利用公式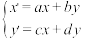 ①(其中
①(其中 ,
, ,
, ,
, 为常数),将点
为常数),将点 变换为点
变换为点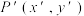 的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由
的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由 ,
, ,
, ,
, 组成的正方形数表
组成的正方形数表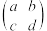 唯一确定,我们将
唯一确定,我们将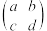 称为二阶矩阵,矩阵通常用大写英文字母
称为二阶矩阵,矩阵通常用大写英文字母 ,
, ,…表示.
,…表示. 中,将点
中,将点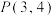 绕原点
绕原点 按逆时针旋转
按逆时针旋转 得到点
得到点 (到原点距离不变),求点
(到原点距离不变),求点 的坐标;
的坐标;
(2)如图,在平面直角坐标系 中,将点
中,将点 绕原点
绕原点 按逆时针旋转
按逆时针旋转 角得到点
角得到点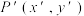 (到原点距离不变),求坐标变换公式及对应的二阶矩阵;
(到原点距离不变),求坐标变换公式及对应的二阶矩阵;
(3)向量 (称为行向量形式),也可以写成
(称为行向量形式),也可以写成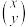 ,这种形式的向量称为列向量,线性变换坐标公式①可以表示为:
,这种形式的向量称为列向量,线性变换坐标公式①可以表示为: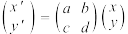 ,则称
,则称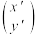 是二阶矩阵
是二阶矩阵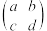 与向量
与向量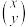 的乘积,设
的乘积,设 是一个二阶矩阵,
是一个二阶矩阵,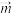 ,
, 是平面上的任意两个向量,求证:
是平面上的任意两个向量,求证: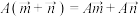 .
.
 中,利用公式
中,利用公式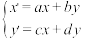 ①(其中
①(其中 ,
, ,
, ,
, 为常数),将点
为常数),将点 变换为点
变换为点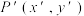 的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由
的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由 ,
, ,
, ,
, 组成的正方形数表
组成的正方形数表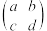 唯一确定,我们将
唯一确定,我们将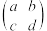 称为二阶矩阵,矩阵通常用大写英文字母
称为二阶矩阵,矩阵通常用大写英文字母 ,
, ,…表示.
,…表示.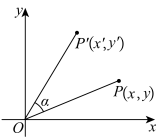
 中,将点
中,将点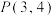 绕原点
绕原点 按逆时针旋转
按逆时针旋转 得到点
得到点 (到原点距离不变),求点
(到原点距离不变),求点 的坐标;
的坐标;(2)如图,在平面直角坐标系
 中,将点
中,将点 绕原点
绕原点 按逆时针旋转
按逆时针旋转 角得到点
角得到点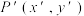 (到原点距离不变),求坐标变换公式及对应的二阶矩阵;
(到原点距离不变),求坐标变换公式及对应的二阶矩阵;(3)向量
 (称为行向量形式),也可以写成
(称为行向量形式),也可以写成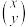 ,这种形式的向量称为列向量,线性变换坐标公式①可以表示为:
,这种形式的向量称为列向量,线性变换坐标公式①可以表示为: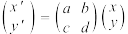 ,则称
,则称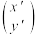 是二阶矩阵
是二阶矩阵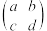 与向量
与向量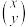 的乘积,设
的乘积,设 是一个二阶矩阵,
是一个二阶矩阵,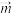 ,
, 是平面上的任意两个向量,求证:
是平面上的任意两个向量,求证: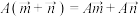 .
.
您最近一年使用:0次
2024-04-12更新
|
2749次组卷
|
12卷引用:安徽省皖江名校联盟2024届高三下学期4月模拟数学试题
安徽省皖江名校联盟2024届高三下学期4月模拟数学试题(已下线)数学(新高考卷02,新题型结构)(已下线)压轴题02圆锥曲线压轴题17题型汇总-1黑龙江省实验中学2024届高三第四次模拟考试数学试题(已下线)4.1 三角函数的定义及同角三角函数(已下线)专题5 解析几何中的新定义压轴大题(过关集训)安徽省2024届新高考数学模拟预测卷(八)(已下线)专题7 线性代数、抽象代数与数论背景的新定义压轴大题(三)【讲】(已下线)重难点突破02 线性代数背景下新定义(四大题型)(已下线)模块五 专题5 全真拔高模拟1(高一人教B版期中)(已下线)模块五 专题5 全真拔高模拟1(苏教版期中研习高一)湖南省湘楚名校2023-2024学年高二下学期5月月考数学试题
名校
解题方法
4 . 由倍角公式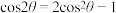 ,可知
,可知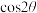 可以表示为
可以表示为 的二次多项式.对于
的二次多项式.对于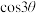 ,我们有
,我们有
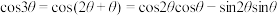
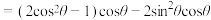

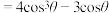
可见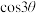 也可以表示成
也可以表示成 的三次多项式.
的三次多项式.
(1)利用上述结论,求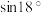 的值;
的值;
(2)化简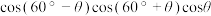 ;并利用此结果求
;并利用此结果求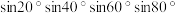 的值;
的值;
(3)已知方程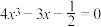 在
在 上有三个根,记为
上有三个根,记为 ,求证:
,求证: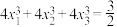 .
.
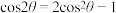 ,可知
,可知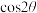 可以表示为
可以表示为 的二次多项式.对于
的二次多项式.对于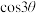 ,我们有
,我们有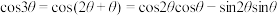
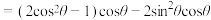

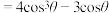
可见
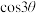 也可以表示成
也可以表示成 的三次多项式.
的三次多项式.(1)利用上述结论,求
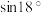 的值;
的值;(2)化简
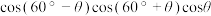 ;并利用此结果求
;并利用此结果求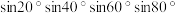 的值;
的值;(3)已知方程
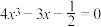 在
在 上有三个根,记为
上有三个根,记为 ,求证:
,求证: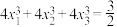 .
.
您最近一年使用:0次
2024-04-11更新
|
1489次组卷
|
8卷引用:4.2 诱导公式与恒等变化
(已下线)4.2 诱导公式与恒等变化(已下线)拔高点突破01 三角函数与解三角形背景下的新定义问题(十大题型)江苏省泰州中学2023-2024学年高一下学期期中考试数学试题(已下线)模块三专题2 新定义专练【高一下人教B版】江西省南昌市第五高级中学2023-2024学年高一下学期期中考试数学试卷(已下线)专题04 三角函数恒等变形综合大题归类 -期末考点大串讲(苏教版(2019))(已下线)作业02 三角恒等变换-【暑假分层作业】(苏教版2019必修第二册)江苏省宿迁青华中学2023-2024学年高一下学期期中数学试题
名校
解题方法
5 . 若函数 的定义域为
的定义域为 ,且存在非零常数
,且存在非零常数 ,使得对任意
,使得对任意 ,都有
,都有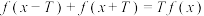 ,则称
,则称 是类周期为
是类周期为 的“类周期函数”.
的“类周期函数”.
(1)若函数 是类周期为1的“类周期函数”,证明:
是类周期为1的“类周期函数”,证明: 是周期函数;
是周期函数;
(2)已知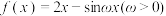 是“类周期函数”,求
是“类周期函数”,求 的值及
的值及 的类周期;
的类周期;
(3)若奇函数 是类周期为
是类周期为 的“类周期函数”,且
的“类周期函数”,且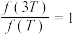 ,求
,求 的值,并给出符合条件的一个
的值,并给出符合条件的一个 .
.
 的定义域为
的定义域为 ,且存在非零常数
,且存在非零常数 ,使得对任意
,使得对任意 ,都有
,都有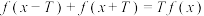 ,则称
,则称 是类周期为
是类周期为 的“类周期函数”.
的“类周期函数”.(1)若函数
 是类周期为1的“类周期函数”,证明:
是类周期为1的“类周期函数”,证明: 是周期函数;
是周期函数;(2)已知
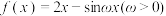 是“类周期函数”,求
是“类周期函数”,求 的值及
的值及 的类周期;
的类周期;(3)若奇函数
 是类周期为
是类周期为 的“类周期函数”,且
的“类周期函数”,且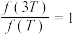 ,求
,求 的值,并给出符合条件的一个
的值,并给出符合条件的一个 .
.
您最近一年使用:0次
6 . 定义: 为实数
为实数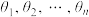 对
对 的“正弦方差”.
的“正弦方差”.
(1)若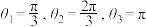 ,则实数
,则实数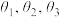 对
对 的“正弦方差”
的“正弦方差” 的值是否是与
的值是否是与 无关的定值,并证明你的结论
无关的定值,并证明你的结论
(2)若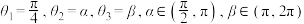 ,若实数
,若实数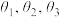 对
对 的“正弦方差”
的“正弦方差” 的值是与
的值是与 无关的定值,求
无关的定值,求 值.
值.
 为实数
为实数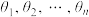 对
对 的“正弦方差”.
的“正弦方差”.(1)若
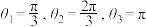 ,则实数
,则实数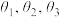 对
对 的“正弦方差”
的“正弦方差” 的值是否是与
的值是否是与 无关的定值,并证明你的结论
无关的定值,并证明你的结论(2)若
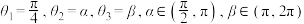 ,若实数
,若实数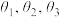 对
对 的“正弦方差”
的“正弦方差” 的值是与
的值是与 无关的定值,求
无关的定值,求 值.
值.
您最近一年使用:0次
名校
7 . 已知函数 的定义域为
的定义域为 ,若存在常数
,若存在常数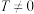 ,使得
,使得 对任意的
对任意的 成立,则称函数
成立,则称函数 是
是 函数.
函数.
(1)判断函数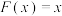 ,
, 是否是
是否是 函数,不必说明理由;
函数,不必说明理由;
(2)若函数 是
是 函数,且
函数,且 是偶函数,求证:函数
是偶函数,求证:函数 是周期函数;
是周期函数;
(3)若函数 是
是 函数.求实数
函数.求实数 的取值范围;
的取值范围;
(4)定义域为 的函数
的函数 同时满足以下三条性质:
同时满足以下三条性质:
①存在 ,使得
,使得 ;
;
②对于任意 ,有
,有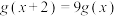 .
.
③ 不是单调函数,但是它图像连续不断,
不是单调函数,但是它图像连续不断,
写出满足上述三个性质的一个函数 ,则
,则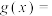 .(不必说明理由)
.(不必说明理由)
 的定义域为
的定义域为 ,若存在常数
,若存在常数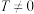 ,使得
,使得 对任意的
对任意的 成立,则称函数
成立,则称函数 是
是 函数.
函数.(1)判断函数
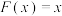 ,
, 是否是
是否是 函数,不必说明理由;
函数,不必说明理由;(2)若函数
 是
是 函数,且
函数,且 是偶函数,求证:函数
是偶函数,求证:函数 是周期函数;
是周期函数;(3)若函数
 是
是 函数.求实数
函数.求实数 的取值范围;
的取值范围;(4)定义域为
 的函数
的函数 同时满足以下三条性质:
同时满足以下三条性质:①存在
 ,使得
,使得 ;
;②对于任意
 ,有
,有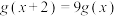 .
.③
 不是单调函数,但是它图像连续不断,
不是单调函数,但是它图像连续不断,写出满足上述三个性质的一个函数
 ,则
,则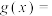 .(不必说明理由)
.(不必说明理由)
您最近一年使用:0次
2023-05-11更新
|
333次组卷
|
3卷引用:专题06 信息迁移型【练】【北京版】
名校
8 . 在数学中,双曲函数是与三角函数类似的函数,最基本的双曲函数是双曲正弦函数与双曲余弦函数,其中双曲正弦函数: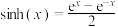 ,双曲余弦函数:
,双曲余弦函数: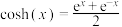 .(e是自然对数的底数,
.(e是自然对数的底数,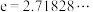 ).双曲函数的定义域是实数集,其自变量的值叫做双曲角,双曲函数出现于某些重要的线性微分方程的解中,譬如说定义悬链线和拉普拉斯方程.
).双曲函数的定义域是实数集,其自变量的值叫做双曲角,双曲函数出现于某些重要的线性微分方程的解中,譬如说定义悬链线和拉普拉斯方程.
(1)计算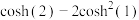 的值;
的值;
(2)类比两角和的余弦公式,写出两角和的双曲余弦公式: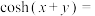 ______,并加以证明;
______,并加以证明;
(3)若对任意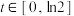 ,关于
,关于 的方程
的方程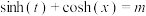 有解,求实数
有解,求实数 的取值范围.
的取值范围.
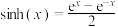 ,双曲余弦函数:
,双曲余弦函数: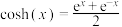 .(e是自然对数的底数,
.(e是自然对数的底数,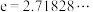 ).双曲函数的定义域是实数集,其自变量的值叫做双曲角,双曲函数出现于某些重要的线性微分方程的解中,譬如说定义悬链线和拉普拉斯方程.
).双曲函数的定义域是实数集,其自变量的值叫做双曲角,双曲函数出现于某些重要的线性微分方程的解中,譬如说定义悬链线和拉普拉斯方程.(1)计算
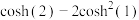 的值;
的值;(2)类比两角和的余弦公式,写出两角和的双曲余弦公式:
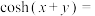 ______,并加以证明;
______,并加以证明;(3)若对任意
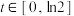 ,关于
,关于 的方程
的方程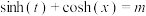 有解,求实数
有解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
9 . 由两角和差公式我们得到倍角公式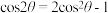 ,实际上
,实际上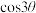 也可以表示为
也可以表示为 的三次多项式.
的三次多项式.
(1)试用 表示
表示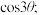
(2)求 的值
的值
(3)已知方程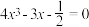 在
在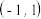 上有三个根,记为
上有三个根,记为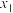 ,
,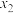 ,
,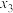 ,求证:
,求证: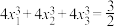 .
.
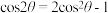 ,实际上
,实际上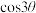 也可以表示为
也可以表示为 的三次多项式.
的三次多项式.(1)试用
 表示
表示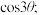
(2)求
 的值
的值
(3)已知方程
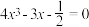 在
在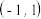 上有三个根,记为
上有三个根,记为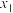 ,
,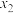 ,
,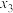 ,求证:
,求证: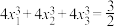 .
.
您最近一年使用:0次
2022-09-25更新
|
1888次组卷
|
4卷引用:福建省福州第十五中学2023届高三10月月考数学试题
福建省福州第十五中学2023届高三10月月考数学试题江苏省南通市海门区2021-2022学年高一下学期期末数学试题(已下线)第5章 三角函数(基础、典型、易错、压轴)分类专项训练(2)【江苏专用】专题02三角函数(第二部分)-高一下学期名校期末好题汇编
名校
10 . 已知函数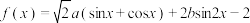 ,(
,(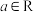 ,
,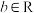 )
)
(1)若 ,
, ,证明:函数
,证明:函数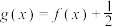 在区间
在区间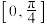 上有且仅有
上有且仅有 个零点;
个零点;
(2)若对于任意的 ,
, 恒成立,求
恒成立,求 的最大值和最小值.
的最大值和最小值.
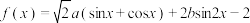 ,(
,(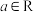 ,
,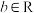 )
)(1)若
 ,
, ,证明:函数
,证明:函数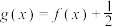 在区间
在区间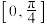 上有且仅有
上有且仅有 个零点;
个零点;(2)若对于任意的
 ,
, 恒成立,求
恒成立,求 的最大值和最小值.
的最大值和最小值.
您最近一年使用:0次
2023-06-29更新
|
1597次组卷
|
8卷引用:江苏省扬州中学2023-2024学年高三上学期10月月考数学试题
江苏省扬州中学2023-2024学年高三上学期10月月考数学试题江苏省镇江第一中学2023-2024学年高三上学期10月月考数学试题江苏省扬州市2022-2023学年高一下学期6月期末数学试题(A)江西省吉安市吉州区部分学校联考2022-2023学年高一下学期7月期末联考数学试题江西省上高中学2022-2023学年高一下学期7月期末数学试题(已下线)模块一 专题3 三角函数的最值问题(高一人教B)(已下线)第五章 三角函数(压轴题专练)-速记·巧练(人教A版2019必修第一册)(已下线)第五章 三角函数(32类知识归纳+38类题型突破)(6) -速记·巧练(人教A版2019必修第一册)



