名校
解题方法
1 . 近几年,我国促进新能源汽车产业发展的政策频出,积极推动新能源汽车市场的迅速发展.某新能源汽车公司为了解其对A型充电桩进行投资后所获得的利润y(单位:百万元)关于投资金额x(单位:百万元)之间的关系,统计后得到10组样本数据,根据统计数据计算得到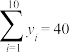 ,
,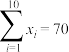 ,利润的方差
,利润的方差 ,投资金额的方差
,投资金额的方差 ,以及样本相关系数
,以及样本相关系数 .
.
(1)根据样本相关系数r判断利润y与投资x的相关性强弱,并求出y关于x的经验回归方程(精确到0.01);
(2)为了解使用A型充电桩的车主性别与使用满意度(分为满意与不满意)的情况,该公司又随机调查了该地区150名使用A型充电桩的车主,其中男性车主有60名对A型充电桩的使用表示满意,有30名对A型充电桩的使用表示不满意;女性车主中有60%对A型充电桩的使用表示满意.将频率视为概率,用样本估计总体.已知该地区一位车主对A型充电桩的使用表示满意,求这位车主是男性的概率.
附:(ⅰ)样本相关系数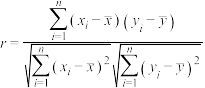 ,当
,当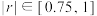 时,相关性较强,当
时,相关性较强,当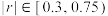 时,相关性一般;
时,相关性一般;
(ⅱ)经验回归方程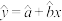 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为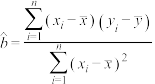 ,
, ;
;
(ⅲ) .
.
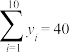 ,
,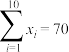 ,利润的方差
,利润的方差 ,投资金额的方差
,投资金额的方差 ,以及样本相关系数
,以及样本相关系数 .
.(1)根据样本相关系数r判断利润y与投资x的相关性强弱,并求出y关于x的经验回归方程(精确到0.01);
(2)为了解使用A型充电桩的车主性别与使用满意度(分为满意与不满意)的情况,该公司又随机调查了该地区150名使用A型充电桩的车主,其中男性车主有60名对A型充电桩的使用表示满意,有30名对A型充电桩的使用表示不满意;女性车主中有60%对A型充电桩的使用表示满意.将频率视为概率,用样本估计总体.已知该地区一位车主对A型充电桩的使用表示满意,求这位车主是男性的概率.
附:(ⅰ)样本相关系数
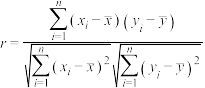 ,当
,当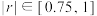 时,相关性较强,当
时,相关性较强,当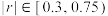 时,相关性一般;
时,相关性一般;(ⅱ)经验回归方程
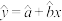 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为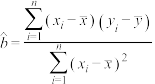 ,
, ;
;(ⅲ)
 .
.
您最近一年使用:0次
名校
2 . 2024年7月26日,第33届夏季奥林匹克运动会在法国巴黎正式开幕.人们在观看奥运比赛的同时,开始投入健身的行列.某兴趣小组为了解成都市不同年龄段的市民每周锻炼时长情况,随机从抽取200人进行调查,得到如下列联表:
(1)试根据 的
的 独立性检验,分析周平均锻炼时长是否与年龄有关?
独立性检验,分析周平均锻炼时长是否与年龄有关?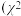 精确到0.001
精确到0.001 ;
;
(2)现从50岁以下的样本中按周平均锻炼时间是否少于4小时,用分层随机抽样法抽取5人做进一步访谈,再从这5人中随机抽取3人填写调查问卷.记抽取3人中周平均锻炼时间不少于4小时的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考公式及数据: ,其中
,其中 .
.
年龄 | 周平均锻炼时长 | 合计 | |
周平均锻炼时间少于4小时 | 周平均锻炼时间不少于4小时 | ||
50岁以下 | 40 | 60 | 100 |
50岁以上(含50) | 25 | 75 | 100 |
合计 | 65 | 135 | 200 |
 的
的 独立性检验,分析周平均锻炼时长是否与年龄有关?
独立性检验,分析周平均锻炼时长是否与年龄有关?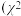 精确到0.001
精确到0.001 ;
;(2)现从50岁以下的样本中按周平均锻炼时间是否少于4小时,用分层随机抽样法抽取5人做进一步访谈,再从这5人中随机抽取3人填写调查问卷.记抽取3人中周平均锻炼时间不少于4小时的人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望. | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
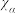 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 .
.
您最近一年使用:0次
2024-09-08更新
|
1299次组卷
|
10卷引用:云南省昆明市第九中学2025届高三上学期9月摸底测试数学试题
云南省昆明市第九中学2025届高三上学期9月摸底测试数学试题云南省昆明市官渡区西南大学官渡实验学校2025届高三上学期期中综合素质测评数学试卷四川省成都市石室成飞中学2025届高三上学期8月月考数学试卷(已下线)全真综合模拟卷(一)(高三大一轮好卷) (提升卷)四川省射洪中学校2024-2025学年高三上学期一模考试数学试题(已下线)专题3 独立性检验 定性与定量(经典好题母题)【练】河北省五校2025届高三上学期第一次联合测评数学试题(已下线)第02讲 成对数据的统计分析(五大题型)(讲义)四川省广安市友实学校2024-2025学年高三上学期10月月考数学试题四川省成都市第十二中学(四川大学附属中学)2025届高三上学期10月月考数学试题
名校
3 . 为提高学生的身体素质,某校决定开展一次学生自愿报名参加的体能训练活动.已知该校学生人数为 ,参加体能训练活动的男生人数为
,参加体能训练活动的男生人数为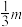 ,不参加体能训练活动的男生人数为
,不参加体能训练活动的男生人数为 ,参加体能训练活动的女生人数为
,参加体能训练活动的女生人数为 .
.
(1)若该校有1200名学生,根据题意完成如图所示的 列联表,并依据小概率值
列联表,并依据小概率值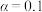 的
的 独立性检验,分析学生参加体能训练活动的意愿与性别是否有关联;
独立性检验,分析学生参加体能训练活动的意愿与性别是否有关联;
(2)按是否参加体能训练活动,采用按比例分配的分层随机抽样方法从该校男生中抽取14人,再从这14人中随机抽取2人,设这2人中参加体能训练活动的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考公式: ,其中
,其中 .
.
 ,参加体能训练活动的男生人数为
,参加体能训练活动的男生人数为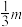 ,不参加体能训练活动的男生人数为
,不参加体能训练活动的男生人数为 ,参加体能训练活动的女生人数为
,参加体能训练活动的女生人数为 .
.(1)若该校有1200名学生,根据题意完成如图所示的
 列联表,并依据小概率值
列联表,并依据小概率值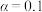 的
的 独立性检验,分析学生参加体能训练活动的意愿与性别是否有关联;
独立性检验,分析学生参加体能训练活动的意愿与性别是否有关联;参加 | 不参加 | 合计 | |
男生 | |||
女生 |
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.参考公式:
 ,其中
,其中 .
. | 0.1 | 0.05 | 0.01 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
4 . 第19届亚运会已于2023年9月23日至10月8日举办,该届亚运会共设40个竞赛大项.其中首次增设了电子竞技项目.与传统的淘汰赛不同,近年来一个新型的赛制“双败赛制”赢得了许多赛事的青睐.传统的淘汰赛失败一场就丧失了冠军争夺的权利,而在双败赛制下,每人或者每个队伍只有失败了两场才会淘汰出局,因此更有容错率.如图,假设最终进入到半决赛有四支队伍,淘汰赛制下会将他们四支队伍两两分组进行比赛,胜者进入到总决赛,总决赛的胜者即为最终的冠军.双败赛制下,两两分组,胜者进入到胜者组,败者进入到败者组,胜者组两个队伍对决的胜者将进入到总决赛,败者进入到败者组.之前进入到败者组的两个队伍对决的败者将直接淘汰,胜者将跟胜者组的败者对决,其中的胜者进入总决赛,最后总决赛的胜者即为冠军,双败赛制下会发现一个有意思的事情,在胜者组中的胜者只要输一场比赛即总决赛就无法拿到冠军,但是其他的队伍却有一次失败的机会,近年来从败者组杀上来拿到冠军的不在少数,因此很多人戏谑这个赛制对强者不公平,是否真的如此呢? .最初分组时AB同组,CD同组.
.最初分组时AB同组,CD同组.
(1)若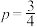 ,在淘汰赛赛制下, A、C获得冠军的概率分别为多少?
,在淘汰赛赛制下, A、C获得冠军的概率分别为多少?
(2)分别计算两种赛制下A获得冠军的概率(用p表示);
(3)根据第2问的结果简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?
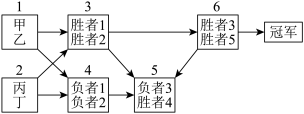
 .最初分组时AB同组,CD同组.
.最初分组时AB同组,CD同组.(1)若
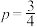 ,在淘汰赛赛制下, A、C获得冠军的概率分别为多少?
,在淘汰赛赛制下, A、C获得冠军的概率分别为多少?(2)分别计算两种赛制下A获得冠军的概率(用p表示);
(3)根据第2问的结果简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?
您最近一年使用:0次
5 . 羽毛球比赛采用21分制,比赛规则如下:一场比赛为三局两胜制,在一局比赛中,每赢一球得1分,先得21分且至少领先2分者获胜,该局比赛结束;当比分打成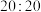 后,以投掷硬币的方式选择发球权,随后得分者拥有发球权,一方领先2分者获胜,该局比赛结束.现有甲、乙两人进行一场21分制的羽毛球比赛,假设甲发球时甲得分的概率为
后,以投掷硬币的方式选择发球权,随后得分者拥有发球权,一方领先2分者获胜,该局比赛结束.现有甲、乙两人进行一场21分制的羽毛球比赛,假设甲发球时甲得分的概率为 ,乙发球时甲得分的概率为
,乙发球时甲得分的概率为 ,各球的比赛结果相互独立,且各局的比赛结果也相互独立.已知第一局目前比分为
,各球的比赛结果相互独立,且各局的比赛结果也相互独立.已知第一局目前比分为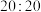 .
.
(1)若再打两个球,这两个球甲得分为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)假设一旦两人比分相等,以投掷硬币的方式选择发球权,求一局比赛甲获胜的概率 ;
;
(3)用 估计每局比赛甲获胜的概率,求该场比赛甲获胜的概率.
估计每局比赛甲获胜的概率,求该场比赛甲获胜的概率.
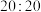 后,以投掷硬币的方式选择发球权,随后得分者拥有发球权,一方领先2分者获胜,该局比赛结束.现有甲、乙两人进行一场21分制的羽毛球比赛,假设甲发球时甲得分的概率为
后,以投掷硬币的方式选择发球权,随后得分者拥有发球权,一方领先2分者获胜,该局比赛结束.现有甲、乙两人进行一场21分制的羽毛球比赛,假设甲发球时甲得分的概率为 ,乙发球时甲得分的概率为
,乙发球时甲得分的概率为 ,各球的比赛结果相互独立,且各局的比赛结果也相互独立.已知第一局目前比分为
,各球的比赛结果相互独立,且各局的比赛结果也相互独立.已知第一局目前比分为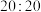 .
.(1)若再打两个球,这两个球甲得分为
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)假设一旦两人比分相等,以投掷硬币的方式选择发球权,求一局比赛甲获胜的概率
 ;
;(3)用
 估计每局比赛甲获胜的概率,求该场比赛甲获胜的概率.
估计每局比赛甲获胜的概率,求该场比赛甲获胜的概率.
您最近一年使用:0次
2024-09-09更新
|
398次组卷
|
2卷引用:云南省2025届高三上学期9月名校联考数学卷
名校
6 . 在某次投篮比赛中,需要投篮四次.第一次投篮命中得1分,第二次投篮命中得2分,第三次和第四次投篮命中均得3分,未命中不得分.甲四次投篮命中的概率分别为 ,且每次投篮能否命中都是相互独立的.
,且每次投篮能否命中都是相互独立的.
(1)求甲四次投篮共得0分的概率;
(2)若规定投篮者四次投篮的总得分不低于7分,则晋级成功.求甲晋级成功的概率.
 ,且每次投篮能否命中都是相互独立的.
,且每次投篮能否命中都是相互独立的.(1)求甲四次投篮共得0分的概率;
(2)若规定投篮者四次投篮的总得分不低于7分,则晋级成功.求甲晋级成功的概率.
您最近一年使用:0次
2024-09-08更新
|
1322次组卷
|
3卷引用:云南省大理州宾川县第四完全中学2024-2025学年高二上学期开学测试数学试题
名校
解题方法
7 . 设集合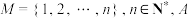 为
为 的非空子集,随机变量
的非空子集,随机变量 分别表示取到子集
分别表示取到子集 中元素的最大值和最小值.
中元素的最大值和最小值.
(1)若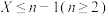 的概率为
的概率为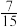 ,求
,求 ;
;
(2)若 ,求
,求 且
且 的概率;
的概率;
(3)已知:对于随机变量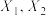 ,有
,有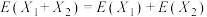 .求随机变量
.求随机变量 的期望
的期望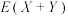 .
.
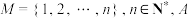 为
为 的非空子集,随机变量
的非空子集,随机变量 分别表示取到子集
分别表示取到子集 中元素的最大值和最小值.
中元素的最大值和最小值.(1)若
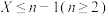 的概率为
的概率为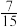 ,求
,求 ;
;(2)若
 ,求
,求 且
且 的概率;
的概率;(3)已知:对于随机变量
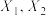 ,有
,有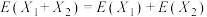 .求随机变量
.求随机变量 的期望
的期望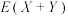 .
.
您最近一年使用:0次
8 . 某区中考体育科目有必选项目和选考项目,其中篮球为一个选考项目.该区体育老师为了了解初中学生的性别和喜欢篮球是否有关,随机调查了该区1000名初中学生,得到成对样本数据的分类统计结果,如下表所示:
(1)依据 的独立性检验,能否认为该区初中学生的性别与喜欢篮球有关联;
的独立性检验,能否认为该区初中学生的性别与喜欢篮球有关联;
(2)用按性别比例分配的分层随机抽样的方法从参与调查的喜欢篮球的600名初中学生中抽取8名学生做进一步调查,将这8名学生作为一个样本,从中随机抽取3人,用X表示随机抽取的3人中女生的人数,求X的分布列和数学期望.
附:参考数据
 ,其中
,其中 .
.
性别 | 是否喜欢篮球 | 合计 | |
喜欢 | 不喜欢 | ||
男生 | 450 | 150 | 600 |
女生 | 150 | 250 | 400 |
合计 | 600 | 400 | 1000 |
(1)依据
 的独立性检验,能否认为该区初中学生的性别与喜欢篮球有关联;
的独立性检验,能否认为该区初中学生的性别与喜欢篮球有关联;(2)用按性别比例分配的分层随机抽样的方法从参与调查的喜欢篮球的600名初中学生中抽取8名学生做进一步调查,将这8名学生作为一个样本,从中随机抽取3人,用X表示随机抽取的3人中女生的人数,求X的分布列和数学期望.
附:参考数据
 ,其中
,其中 .
.
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-08-30更新
|
203次组卷
|
2卷引用:云南省长水教育集团2024-2025学年高三上学期10月质量检测数学试题
解题方法
9 . 一个袋子中有10个大小相同的球,其中黄球6个,红球4个,每次从袋中随机摸出1个球,摸出的球不再放回.
(1)求第2次摸到红球的概率;
(2)对于事件 ,当
,当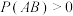 时,证明:
时,证明: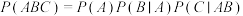 ;
;
(3)利用(2)中的结论,求第 次都摸到红球的概率.
次都摸到红球的概率.
(1)求第2次摸到红球的概率;
(2)对于事件
 ,当
,当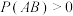 时,证明:
时,证明: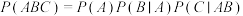 ;
;(3)利用(2)中的结论,求第
 次都摸到红球的概率.
次都摸到红球的概率.
您最近一年使用:0次
2024-08-04更新
|
88次组卷
|
2卷引用:云南省保山市实验中学2023-2024学年高二下学期月考测评(八)数学试题
10 . 为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了抽样调查,从全体学生中随机抽取男女各100名学生,经统计,抽查数据如下表:
(1)依据小概率值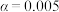 的独立性检验,分析性别与体育锻炼的经常性是否有关?
的独立性检验,分析性别与体育锻炼的经常性是否有关?
(2)为提高学生体育锻炼的积极性,学校决定在上述经常参加体育锻炼的学生中,按性别分层抽样随机抽取7名同学组成体育锻炼宣传小组,并从这7名同学中选出3人担任宣传组长,记男生担任宣传组长的人数为 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
附: .(其中,
.(其中, 为样本容量)
为样本容量)
| 性别 | 锻炼 | 合计 | |
| 经常 | 不经常 | ||
| 男生 | 60 | 40 | 100 |
| 女生 | 80 | 20 | 100 |
| 合计 | 140 | 60 | 200 |
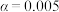 的独立性检验,分析性别与体育锻炼的经常性是否有关?
的独立性检验,分析性别与体育锻炼的经常性是否有关?(2)为提高学生体育锻炼的积极性,学校决定在上述经常参加体育锻炼的学生中,按性别分层抽样随机抽取7名同学组成体育锻炼宣传小组,并从这7名同学中选出3人担任宣传组长,记男生担任宣传组长的人数为
 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.附:
 .(其中,
.(其中, 为样本容量)
为样本容量) | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次



