解题方法
1 . 如图,在四棱锥 中,底面ABCD为平行四边形,平面
中,底面ABCD为平行四边形,平面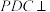 平面ABCD,
平面ABCD,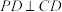 ,
,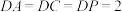 ,点M为棱PC中点,平面ABM与棱PD交于点N.
,点M为棱PC中点,平面ABM与棱PD交于点N.

(1)求证:N是棱PD的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求:
(i)二面角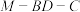 的余弦值;
的余弦值;
(ii)在棱PA上是否存在点Q,使得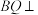 平面BDM?若存在,求出
平面BDM?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
条件①: ;
;
条件②: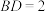 .
.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
 中,底面ABCD为平行四边形,平面
中,底面ABCD为平行四边形,平面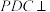 平面ABCD,
平面ABCD,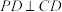 ,
,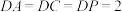 ,点M为棱PC中点,平面ABM与棱PD交于点N.
,点M为棱PC中点,平面ABM与棱PD交于点N.
(1)求证:N是棱PD的中点;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求:
(i)二面角
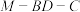 的余弦值;
的余弦值;(ii)在棱PA上是否存在点Q,使得
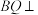 平面BDM?若存在,求出
平面BDM?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.条件①:
 ;
;条件②:
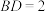 .
.注:如果选择条件①和条件②分别解答,按第一个解答计分.
您最近一年使用:0次
解题方法
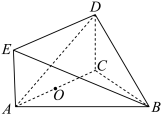
2 . 如图,平面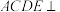 平面
平面 ,四边形
,四边形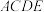 为矩形,
为矩形, 为正三角形,
为正三角形, ,
, 为
为 的中点,
的中点, 为
为 上一动点
上一动点
(1)当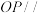 平面
平面 时,求
时,求 的值;
的值;
(2)在(1)的条件下,求 与平面
与平面 所成角的正弦值
所成角的正弦值
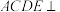 平面
平面 ,四边形
,四边形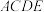 为矩形,
为矩形, 为正三角形,
为正三角形, ,
, 为
为 的中点,
的中点, 为
为 上一动点
上一动点
(1)当
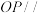 平面
平面 时,求
时,求 的值;
的值;(2)在(1)的条件下,求
 与平面
与平面 所成角的正弦值
所成角的正弦值
您最近一年使用:0次
2023-11-30更新
|
569次组卷
|
4卷引用:河南省新乡市2024届高三一模数学试题
河南省新乡市2024届高三一模数学试题山西省吕梁市兴县友兰中学2024届高三上学期12月月考数学试题(已下线)模块五 专题5 期末全真模拟(拔高卷1)期末终极研习室(高二人教A版)(已下线)模块一 专题1 《立体几何》单元检测篇 B提升卷
解题方法
3 . 如图,在四棱锥 中,底面
中,底面 为矩形,平面
为矩形,平面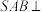 平面
平面 ,
,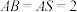 ,
, ,
,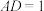 ,
, 为
为 的重心,
的重心, .
.
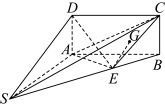
(1)当直线 平面
平面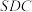 时,求
时,求 的值;
的值;
(2)当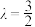 时,求平面
时,求平面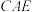 与平面
与平面 的夹角的大小.
的夹角的大小.
 中,底面
中,底面 为矩形,平面
为矩形,平面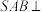 平面
平面 ,
,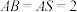 ,
, ,
,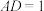 ,
, 为
为 的重心,
的重心, .
.
(1)当直线
 平面
平面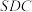 时,求
时,求 的值;
的值;(2)当
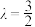 时,求平面
时,求平面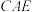 与平面
与平面 的夹角的大小.
的夹角的大小.
您最近一年使用:0次
名校
解题方法
4 . 如图,在四棱锥 中,
中,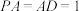 ,
,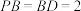 ,
,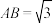 ,
, ,且
,且 .
.

(1)若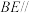 平面
平面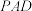 ,证明:点
,证明:点 为棱
为棱 的中点;
的中点;
(2)已知二面角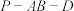 的大小为
的大小为 ,求:平面
,求:平面 和平面
和平面 夹角的余弦值.
夹角的余弦值.
 中,
中,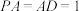 ,
,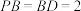 ,
,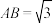 ,
, ,且
,且 .
.
(1)若
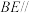 平面
平面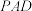 ,证明:点
,证明:点 为棱
为棱 的中点;
的中点;(2)已知二面角
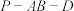 的大小为
的大小为 ,求:平面
,求:平面 和平面
和平面 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
名校
解题方法
5 . 如图1,矩形 ,
, ,
, ,点E为
,点E为 的中点,将
的中点,将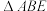 沿直线
沿直线 折起至平面
折起至平面 平面
平面 (如图2),点M在线段
(如图2),点M在线段 上,
上,
 平面
平面 .
.

(1)求证: ;
;
(2)求点B到面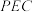 的距离;
的距离;
(3)若在棱 ,
, 分别取中点F,G,试判断点M与平面
分别取中点F,G,试判断点M与平面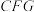 的关系,并说明理由.
的关系,并说明理由.
 ,
, ,
, ,点E为
,点E为 的中点,将
的中点,将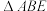 沿直线
沿直线 折起至平面
折起至平面 平面
平面 (如图2),点M在线段
(如图2),点M在线段 上,
上,
 平面
平面 .
.
(1)求证:
 ;
;(2)求点B到面
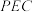 的距离;
的距离;(3)若在棱
 ,
, 分别取中点F,G,试判断点M与平面
分别取中点F,G,试判断点M与平面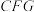 的关系,并说明理由.
的关系,并说明理由.
您最近一年使用:0次
名校
解题方法
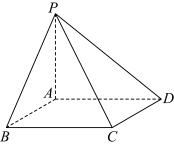
6 . 如图,四边形 为正方形,点
为正方形,点 不在
不在 所在平面上,且直线
所在平面上,且直线 平面
平面 ,
,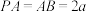 ,
, 为线段
为线段 的中点.
的中点.
(1)若 为线段
为线段 的中点,求直线
的中点,求直线 和平面
和平面 所成角的大小;
所成角的大小;
(2)若点 在线段
在线段 上移动,当直线
上移动,当直线 平面
平面 时,求
时,求 的面积.
的面积.
 为正方形,点
为正方形,点 不在
不在 所在平面上,且直线
所在平面上,且直线 平面
平面 ,
,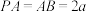 ,
, 为线段
为线段 的中点.
的中点.
(1)若
 为线段
为线段 的中点,求直线
的中点,求直线 和平面
和平面 所成角的大小;
所成角的大小;(2)若点
 在线段
在线段 上移动,当直线
上移动,当直线 平面
平面 时,求
时,求 的面积.
的面积.
您最近一年使用:0次
名校
7 . 已知矩形ABCD中,点E在边CD上,且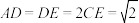 .现将
.现将 沿AE向上翻折,使点D到点P的位置,构成如图所示的四棱锥
沿AE向上翻折,使点D到点P的位置,构成如图所示的四棱锥 .
.
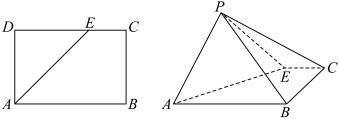
(1)若点F在线段AP上,且
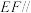 平面PBC,求
平面PBC,求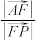 的值;
的值;(2)若
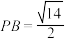 ,求锐二面角
,求锐二面角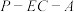 的余弦值.
的余弦值.
您最近一年使用:0次
2023-10-19更新
|
1569次组卷
|
4卷引用:江西省南昌市江西师范大学附属中学2024届高三上学期数学素养测试试题
江西省南昌市江西师范大学附属中学2024届高三上学期数学素养测试试题云南省2024届高三上学期新高考联考数学试题(已下线)黄金卷03(已下线)江苏省淮阴中学等四校2024届高三下学期期初测试联考数学试卷
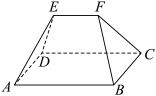
8 . 我国古代数学名著《九章算术》中记载:“刍(chú)薨(méng)者,下有袤有广,而上有袤无广.刍,草也. 薨,窟盖也。”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍薨的字面意思为茅草屋顶.”现有一个“刍薨”如图所示,四边形 为正方形,四边形
为正方形,四边形 、
、 为两个全等的等腰梯形,
为两个全等的等腰梯形, ,
, ,
,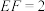 ,
,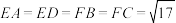 .
.
(1)设过点 且与直线
且与直线 垂直的平面为平面
垂直的平面为平面 ,且平面
,且平面 与直线
与直线 、
、 分别交于
分别交于 、
、 两点,求
两点,求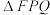 的周长;
的周长;
(2)点 在线段
在线段 上且满足
上且满足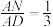 .试问:在线段
.试问:在线段 上是否存在点
上是否存在点 ,使
,使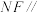 平面
平面 ?若存在,求出
?若存在,求出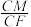 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 为正方形,四边形
为正方形,四边形 、
、 为两个全等的等腰梯形,
为两个全等的等腰梯形, ,
, ,
,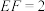 ,
,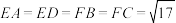 .
.
(1)设过点
 且与直线
且与直线 垂直的平面为平面
垂直的平面为平面 ,且平面
,且平面 与直线
与直线 、
、 分别交于
分别交于 、
、 两点,求
两点,求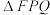 的周长;
的周长;(2)点
 在线段
在线段 上且满足
上且满足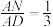 .试问:在线段
.试问:在线段 上是否存在点
上是否存在点 ,使
,使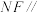 平面
平面 ?若存在,求出
?若存在,求出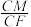 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
9 . 如图,在四棱锥 中,平面
中,平面 平面
平面 ,
, 为
为 的中点,
的中点, ,
,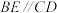 ,
, ,
,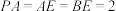 ,
,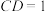 .
. 到平面
到平面 的距离;
的距离;
(2)求直线 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(3)在线段 上是否存在点
上是否存在点 ,使得
,使得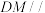 平面
平面 ?若存在,求出点
?若存在,求出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
 中,平面
中,平面 平面
平面 ,
, 为
为 的中点,
的中点, ,
,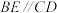 ,
, ,
,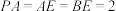 ,
,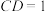 .
.
 到平面
到平面 的距离;
的距离;(2)求直线
 与平面
与平面 所成角的余弦值;
所成角的余弦值;(3)在线段
 上是否存在点
上是否存在点 ,使得
,使得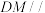 平面
平面 ?若存在,求出点
?若存在,求出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
您最近一年使用:0次
2023-10-01更新
|
1471次组卷
|
13卷引用:山东省青岛第五十八中学2022-2023学年高二上学期10月月考数学试题
山东省青岛第五十八中学2022-2023学年高二上学期10月月考数学试题山东省青岛市青岛第一中学2023-2024学年高二上学期10月月考数学试题广东省广州市广东实验中学越秀学校2023-2024学年高二上学期期中数学试题内蒙古自治区优质高中联考2023-2024学年高二上学期11月期中数学试题河南省焦作市宇华实验学校2023-2024学年高二上学期期末拔高数学试题(二)河南省焦作市宇华实验学校2023-2024学年高二上学期期末拓展数学试题(已下线)2023-2024学年高二上学期期中数学模拟试卷(原卷版)江苏省扬州市宝应县氾水高级中学2023-2024学年高二下学期3月阶段调研考试数学试题江苏省连云港市七校2023-2024学年高二下学期期中考试数学试题(已下线)江苏省连云港市七校2023-2024学年高二下学期期中考试数学试题变式题16-19山东省枣庄市第三中学2024-2025学年高二上学期第一次月考数学试题山东省青岛第五十八中学2024-2025学年高二上学期阶段性模块检测数学试题广东省佛山市石门中学2024-2025学年高二上学期第一次月考数学试题
10 . 如图,在直三棱柱 中,
中, ,
, ,
,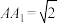 ,点
,点 分别是
分别是 的中点,点
的中点,点 是线段
是线段 上一点,且
上一点,且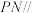 平面
平面 .
.

(1)求证:点 是线段
是线段 的中点;
的中点;
(2)求二面角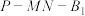 的余弦值.
的余弦值.
 中,
中, ,
, ,
,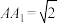 ,点
,点 分别是
分别是 的中点,点
的中点,点 是线段
是线段 上一点,且
上一点,且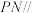 平面
平面 .
.
(1)求证:点
 是线段
是线段 的中点;
的中点;(2)求二面角
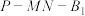 的余弦值.
的余弦值.
您最近一年使用:0次



