名校
1 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.
例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵ ,∴
,∴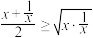 ,即
,即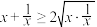 ,∴
,∴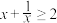 ,
,
当且仅当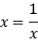 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)已知如 ,求下列各式的值:
,求下列各式的值:
①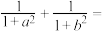 ___________.
___________.
②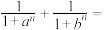 ___________.
___________.
(2)若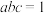 ,解方程
,解方程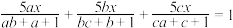 .
.
(3)若正数a、b满足 ,求
,求 的最小值.
的最小值.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式
 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.例如:在
 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵
 ,∴
,∴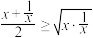 ,即
,即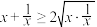 ,∴
,∴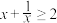 ,
,当且仅当
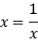 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)已知如
 ,求下列各式的值:
,求下列各式的值:①
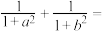 ___________.
___________.②
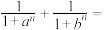 ___________.
___________.(2)若
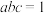 ,解方程
,解方程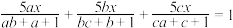 .
.(3)若正数a、b满足
 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2021-10-29更新
|
530次组卷
|
3卷引用:江苏省南通中学2020-2021学年高一上学期开学考试数学试题
江苏省南通中学2020-2021学年高一上学期开学考试数学试题江西省南昌市第二中学2023-2024学年高一上学期月考数学试题(一)(已下线)第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)
名校
2 . 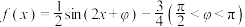 ,且
,且 .
.
(1)方程 在
在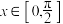 有且仅有一个解,求
有且仅有一个解,求 的取值范围.
的取值范围.
(2)设 ,对
,对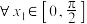 ,总
,总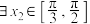 ,使
,使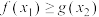 成立,求
成立,求 的范围.
的范围.
(3)若 与
与 的图象关于
的图象关于 对称,求不等式
对称,求不等式 的解集.
的解集.
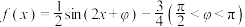 ,且
,且 .
.(1)方程
 在
在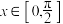 有且仅有一个解,求
有且仅有一个解,求 的取值范围.
的取值范围.(2)设
 ,对
,对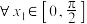 ,总
,总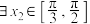 ,使
,使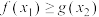 成立,求
成立,求 的范围.
的范围.(3)若
 与
与 的图象关于
的图象关于 对称,求不等式
对称,求不等式 的解集.
的解集.
您最近一年使用:0次
2023-05-21更新
|
1192次组卷
|
6卷引用:辽宁省沈阳市第十一中学2022-2023学年高一下学期4月月考数学试题
辽宁省沈阳市第十一中学2022-2023学年高一下学期4月月考数学试题江西省吉安市双校联盟2022-2023学年高一下学期期中考试数学试题(已下线)专题5.9 三角函数全章八类必考压轴题-举一反三系列(已下线)专题5.4 三角函数的图象与性质-举一反三系列(已下线)第七章 三角函数(压轴题专练)-单元速记·巧练(沪教版2020必修第二册)(已下线)模块四 专题2 重组综合练(江西)(北师版高一期中)
名校
3 . 已知函数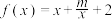 (
( 为常数)
为常数)
(1)定义:区间 的长度为
的长度为 ,若
,若 ,问是否存在区间
,问是否存在区间 ,使得
,使得 时,
时, 的值域为
的值域为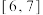 ,若存在,求出此区间长度的最大值;
,若存在,求出此区间长度的最大值;
(2)解关于 的不等式:
的不等式: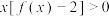 ;
;
(3)求函数 在
在 上的最小值.
上的最小值.
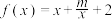 (
( 为常数)
为常数)(1)定义:区间
 的长度为
的长度为 ,若
,若 ,问是否存在区间
,问是否存在区间 ,使得
,使得 时,
时, 的值域为
的值域为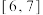 ,若存在,求出此区间长度的最大值;
,若存在,求出此区间长度的最大值;(2)解关于
 的不等式:
的不等式: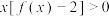 ;
;(3)求函数
 在
在 上的最小值.
上的最小值.
您最近一年使用:0次
名校
解题方法
4 . 为了求一个棱长为 的正四面体的体积,某同学设计如下解法.
的正四面体的体积,某同学设计如下解法.
解:构造一个棱长为1的正方体,如图1:则四面体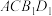 为棱长是
为棱长是 的正四面体,且有
的正四面体,且有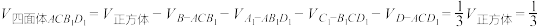 .
.

(1)类似此解法,如图2,一个相对棱长都相等的四面体,其三组棱长分别为 ,
, ,
,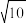 ,求此四面体的体积;
,求此四面体的体积;
(2)对棱分别相等的四面体 中,
中, ,
, ,
, .求证:这个四面体的四个面都是锐角三角形;
.求证:这个四面体的四个面都是锐角三角形;
(3)有4条长为2的线段和2条长为 的线段,用这6条线段作为棱且长度为
的线段,用这6条线段作为棱且长度为 的线段不相邻,构成一个三棱锥,问
的线段不相邻,构成一个三棱锥,问 为何值时,构成三棱锥体积最大,最大值为多少?
为何值时,构成三棱锥体积最大,最大值为多少?
[参考公式:三元均值不等式 及变形
及变形 ,当且仅当
,当且仅当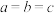 时取得等号]
时取得等号]
 的正四面体的体积,某同学设计如下解法.
的正四面体的体积,某同学设计如下解法.解:构造一个棱长为1的正方体,如图1:则四面体
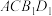 为棱长是
为棱长是 的正四面体,且有
的正四面体,且有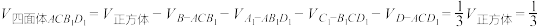 .
.
(1)类似此解法,如图2,一个相对棱长都相等的四面体,其三组棱长分别为
 ,
, ,
,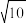 ,求此四面体的体积;
,求此四面体的体积;(2)对棱分别相等的四面体
 中,
中, ,
, ,
, .求证:这个四面体的四个面都是锐角三角形;
.求证:这个四面体的四个面都是锐角三角形;(3)有4条长为2的线段和2条长为
 的线段,用这6条线段作为棱且长度为
的线段,用这6条线段作为棱且长度为 的线段不相邻,构成一个三棱锥,问
的线段不相邻,构成一个三棱锥,问 为何值时,构成三棱锥体积最大,最大值为多少?
为何值时,构成三棱锥体积最大,最大值为多少?[参考公式:三元均值不等式
 及变形
及变形 ,当且仅当
,当且仅当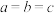 时取得等号]
时取得等号]
您最近一年使用:0次
2021-07-15更新
|
814次组卷
|
2卷引用:重庆市西南大学附属中学2020-2021学年高一下学期期末数学试题
名校
解题方法
5 . 已知二次函数 (
(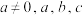 为常数)的对称轴为
为常数)的对称轴为 ,其图像如图所示,则下列选项正确的有( )
,其图像如图所示,则下列选项正确的有( )
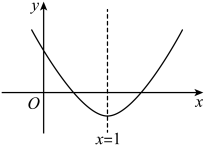
 (
(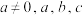 为常数)的对称轴为
为常数)的对称轴为 ,其图像如图所示,则下列选项正确的有( )
,其图像如图所示,则下列选项正确的有( )
A.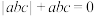 |
B.当 时,函数的最大值为 时,函数的最大值为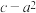 |
C.关于 的不等式 的不等式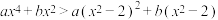 的解为 的解为 或 或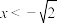 |
D.若关于 的函数 的函数 与关于 与关于 的函数 的函数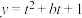 有相同的最小值,则 有相同的最小值,则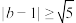 |
您最近一年使用:0次
2023-03-20更新
|
1665次组卷
|
12卷引用:湖北省武汉市华中师范大学第一附属中学2021年高中自主招生考试数学试题
湖北省武汉市华中师范大学第一附属中学2021年高中自主招生考试数学试题(已下线)高一上学期第一次月考数学试卷(提高篇)-举一反三系列(已下线)2.3 二次函数与一元二次方程、不等式(AB分层训练)-【冲刺满分】(已下线)专题2.7 一元二次函数、方程和不等式全章综合测试卷(提高篇)-举一反三系列福建省宁德第一中学2023-2024学年高一上学期入学考试数学试题重庆市西南大学附属中学校2023-2024学年高一上学期9月定时检测(一)数学试题福建省厦门第一中学2023-2024学年高一上学期第一次适应性练习数学试题湖南省株洲市南方中学2023-2024学年高一上学期10月月考数学试题广东省四校(珠海市实验中学、东莞市第六高级中学、河源高级中学、中山市实验中学)2023-2024学年高一上学期10月联考数学试题湖南省邵阳市2023-2024学年高一上学期拔尖创新人才早期培养竞赛(初赛)数学试题(已下线)第二章 函数的概念与性质 第四节 二次函数(B素养提升卷)(已下线)一次函数与二次函数
解题方法
6 . 已知函数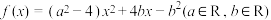 .
.
(1)问题:若关于x的方程 ______,求实数a的取值范围;
______,求实数a的取值范围;
从下面给出的①②③三个条件中任选一个,补充到上面的问题中,并进行解答.
①有两个不等正实根;②有两个相异负实根;③有1个正实根和1个负实根.
(若选择多个方案分别解答,则按第一个解答记分.)
(2)当 时,解关于x的不等式
时,解关于x的不等式 ;
;
(3)当 时,若关于x的不等式
时,若关于x的不等式 的解集中有且仅有2023个整数,求实数a的取值范围.
的解集中有且仅有2023个整数,求实数a的取值范围.
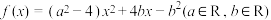 .
.(1)问题:若关于x的方程
 ______,求实数a的取值范围;
______,求实数a的取值范围;从下面给出的①②③三个条件中任选一个,补充到上面的问题中,并进行解答.
①有两个不等正实根;②有两个相异负实根;③有1个正实根和1个负实根.
(若选择多个方案分别解答,则按第一个解答记分.)
(2)当
 时,解关于x的不等式
时,解关于x的不等式 ;
;(3)当
 时,若关于x的不等式
时,若关于x的不等式 的解集中有且仅有2023个整数,求实数a的取值范围.
的解集中有且仅有2023个整数,求实数a的取值范围.
您最近一年使用:0次
名校
7 . 已知定义在 上的函数
上的函数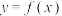 ,若存在实数
,若存在实数 ,
, ,
, 使得
使得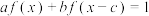 对任意的实数
对任意的实数 恒成立,则称函数
恒成立,则称函数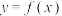 为“
为“ 函数”;
函数”;
(1)已知 ,判断它是否为“
,判断它是否为“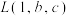 函数”;
函数”;
(2)若函数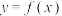 是“
是“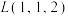 函数”,当
函数”,当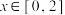 ,
, ,求
,求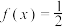 在
在 上的解.
上的解.
(3)证明函数 为“
为“ 函数”并求所有符合条件的
函数”并求所有符合条件的 、
、 、
、 .
.
 上的函数
上的函数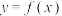 ,若存在实数
,若存在实数 ,
, ,
, 使得
使得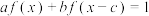 对任意的实数
对任意的实数 恒成立,则称函数
恒成立,则称函数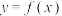 为“
为“ 函数”;
函数”;(1)已知
 ,判断它是否为“
,判断它是否为“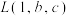 函数”;
函数”;(2)若函数
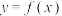 是“
是“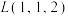 函数”,当
函数”,当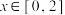 ,
, ,求
,求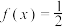 在
在 上的解.
上的解.(3)证明函数
 为“
为“ 函数”并求所有符合条件的
函数”并求所有符合条件的 、
、 、
、 .
.
您最近一年使用:0次
名校
8 . 在面积为 的
的 中,内角
中,内角 所对的边分别为
所对的边分别为 ,且
,且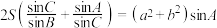 .
.
(1)若 为锐角三角形,
为锐角三角形, 是关于
是关于 的方程
的方程 的解,求
的解,求 的取值范围;
的取值范围;
(2)若 且
且 的外接圆的直径为8,
的外接圆的直径为8, 分别在线段
分别在线段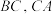 上运动(包括端点),
上运动(包括端点), 为边
为边 的中点,且
的中点,且 ,
,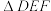 的面积为
的面积为 .令
.令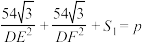 ,求
,求 的最小值.
的最小值.
 的
的 中,内角
中,内角 所对的边分别为
所对的边分别为 ,且
,且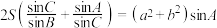 .
.(1)若
 为锐角三角形,
为锐角三角形, 是关于
是关于 的方程
的方程 的解,求
的解,求 的取值范围;
的取值范围;(2)若
 且
且 的外接圆的直径为8,
的外接圆的直径为8, 分别在线段
分别在线段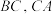 上运动(包括端点),
上运动(包括端点), 为边
为边 的中点,且
的中点,且 ,
,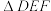 的面积为
的面积为 .令
.令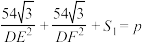 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
9 . 已知向量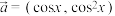 ,
,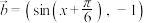 .设函数
.设函数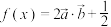 ,
, .
.
(1)求函数 的解析式及其单调增区间;
的解析式及其单调增区间;
(2)设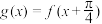 ,若方程
,若方程 在
在 上有两个不同的解
上有两个不同的解 ,求实数
,求实数 的取值范围,并求
的取值范围,并求 的值.
的值.
(3)若将 的图像上的所有点向左平移
的图像上的所有点向左平移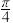 个单位,再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数
个单位,再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数 的图像.当
的图像.当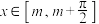 (其中
(其中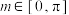 )时,记函数
)时,记函数 的最大值与最小值分别为
的最大值与最小值分别为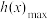 与
与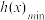 ,设
,设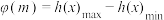 ,求函数
,求函数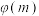 的解析式.
的解析式.
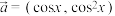 ,
,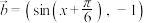 .设函数
.设函数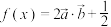 ,
, .
.(1)求函数
 的解析式及其单调增区间;
的解析式及其单调增区间;(2)设
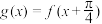 ,若方程
,若方程 在
在 上有两个不同的解
上有两个不同的解 ,求实数
,求实数 的取值范围,并求
的取值范围,并求 的值.
的值.(3)若将
 的图像上的所有点向左平移
的图像上的所有点向左平移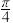 个单位,再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数
个单位,再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数 的图像.当
的图像.当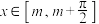 (其中
(其中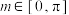 )时,记函数
)时,记函数 的最大值与最小值分别为
的最大值与最小值分别为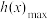 与
与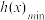 ,设
,设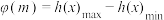 ,求函数
,求函数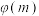 的解析式.
的解析式.
您最近一年使用:0次
2023-03-26更新
|
849次组卷
|
2卷引用:江苏省常州市联盟学校2022-2023学年高一下学期3月学情调研数学试题



