1 . 已知函数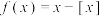 (
( 表示不超过
表示不超过 的最大整数),
的最大整数), ,若对任意的
,若对任意的 ,总存在三个不相等的实数
,总存在三个不相等的实数 ,
, ,
, ,使得
,使得 ,则
,则 的取值范围是( )
的取值范围是( )
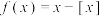 (
( 表示不超过
表示不超过 的最大整数),
的最大整数), ,若对任意的
,若对任意的 ,总存在三个不相等的实数
,总存在三个不相等的实数 ,
, ,
, ,使得
,使得 ,则
,则 的取值范围是( )
的取值范围是( )A.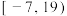 | B.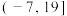 | C.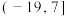 | D.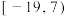 |
您最近一年使用:0次
解题方法
2 . 定义 为不超过
为不超过 的最大整数,区间
的最大整数,区间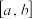 (或
(或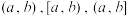 )的长度记为
)的长度记为 .若关于
.若关于 的不等式
的不等式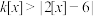 的解集对应区间的长度为2,则实数
的解集对应区间的长度为2,则实数 的取值范围为( )
的取值范围为( )
 为不超过
为不超过 的最大整数,区间
的最大整数,区间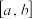 (或
(或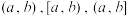 )的长度记为
)的长度记为 .若关于
.若关于 的不等式
的不等式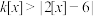 的解集对应区间的长度为2,则实数
的解集对应区间的长度为2,则实数 的取值范围为( )
的取值范围为( )A.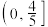 | B.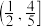 |
C.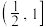 | D.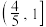 |
您最近一年使用:0次
3 . 已知函数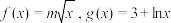 ,若存在两条不同的直线与曲线
,若存在两条不同的直线与曲线 和
和 均相切,则实数
均相切,则实数 的取值范围为
的取值范围为______ .
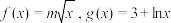 ,若存在两条不同的直线与曲线
,若存在两条不同的直线与曲线 和
和 均相切,则实数
均相切,则实数 的取值范围为
的取值范围为
您最近一年使用:0次
4 . 已知函数 与
与 的导函数分别为
的导函数分别为 与
与 ,且
,且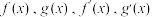 的定义域均为
的定义域均为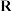 ,
,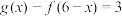 ,
,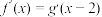 ,
,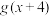 为奇函数,则( )
为奇函数,则( )
 与
与 的导函数分别为
的导函数分别为 与
与 ,且
,且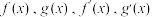 的定义域均为
的定义域均为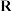 ,
,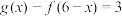 ,
,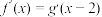 ,
,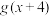 为奇函数,则( )
为奇函数,则( )A.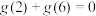 | B.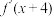 为偶函数 为偶函数 |
C. | D.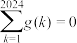 |
您最近一年使用:0次
解题方法
5 . 已知函数 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求
时,求 的极值;
的极值;
(3)若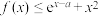 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 .
.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)当
 时,求
时,求 的极值;
的极值;(3)若
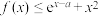 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
6 . 已知函数 有两个零点
有两个零点 .
.
(1)求实数a的取值范围;
(2)求证: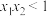 ;
;
 有两个零点
有两个零点 .
.(1)求实数a的取值范围;
(2)求证:
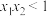 ;
;
您最近一年使用:0次
解题方法
7 . 若对任意 ,不等式
,不等式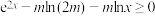 恒成立,则实数m的最大值
恒成立,则实数m的最大值________ .
 ,不等式
,不等式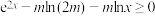 恒成立,则实数m的最大值
恒成立,则实数m的最大值
您最近一年使用:0次
8 . 已知函数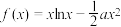 ,
, .
.
(1)求函数 的极值点个数;
的极值点个数;
(2)若函数 存在极大值点
存在极大值点 ,且使得
,且使得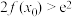 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
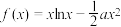 ,
, .
.(1)求函数
 的极值点个数;
的极值点个数;(2)若函数
 存在极大值点
存在极大值点 ,且使得
,且使得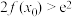 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 若至少由两个元素构成的有限集合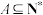 ,且对于任意的
,且对于任意的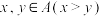 ,都有
,都有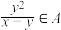 ,则称
,则称 为“
为“ 集合”.
集合”.
(1)判断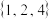 是否为“
是否为“ 集合”,说明理由;
集合”,说明理由;
(2)若双元素集 为“
为“ 集合”,且
集合”,且 ,求所有满足条件的集合
,求所有满足条件的集合 ;
;
(3)求所有满足条件的“ 集合”.
集合”.
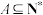 ,且对于任意的
,且对于任意的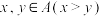 ,都有
,都有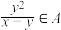 ,则称
,则称 为“
为“ 集合”.
集合”.(1)判断
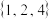 是否为“
是否为“ 集合”,说明理由;
集合”,说明理由;(2)若双元素集
 为“
为“ 集合”,且
集合”,且 ,求所有满足条件的集合
,求所有满足条件的集合 ;
;(3)求所有满足条件的“
 集合”.
集合”.
您最近一年使用:0次
昨日更新
|
250次组卷
|
4卷引用:安徽省合肥市第四中学2025届高三上学期教学诊断检测(三)数学试题
24-25高二上·安徽阜阳·阶段练习
名校
解题方法
10 . 在四面体 中,
中,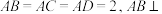 平面
平面 ,
,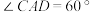 ,点
,点 分别为棱
分别为棱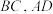 上的点,且
上的点,且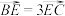 ,
,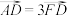 ,则直线
,则直线 与直线
与直线 夹角的余弦值为( )
夹角的余弦值为( )
 中,
中,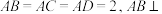 平面
平面 ,
,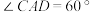 ,点
,点 分别为棱
分别为棱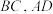 上的点,且
上的点,且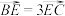 ,
,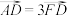 ,则直线
,则直线 与直线
与直线 夹角的余弦值为( )
夹角的余弦值为( )A.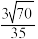 | B. | C.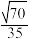 | D. |
您最近一年使用:0次
昨日更新
|
310次组卷
|
3卷引用:安徽省临泉第一中学等校2024-2025学年高二上学期10月联考数学试题(B卷)
(已下线)安徽省临泉第一中学等校2024-2025学年高二上学期10月联考数学试题(B卷)安徽省县中联盟2024-2025学年高二上学期10月月考数学B卷河北省沧州市八县2024-2025学年高二上学期10月期中联考数学试题



