名校
解题方法
1 . 球面三角学是研究球面三角形的边、角关系的一门学科.如图,球 的半径为
的半径为 ,
, ,
, ,
, 为球面上三点,劣弧
为球面上三点,劣弧 的弧长记为
的弧长记为 ,设
,设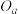 表示以
表示以 为圆心,且过
为圆心,且过 ,
, 的圆,同理,圆
的圆,同理,圆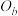 ,
, 的劣弧
的劣弧 ,
, 的弧长分别记为
的弧长分别记为 ,
, ,曲面
,曲面 (阴影部分)叫做曲面三角形,若
(阴影部分)叫做曲面三角形,若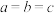 ,则称其为曲面等边三角形,线段
,则称其为曲面等边三角形,线段 ,
, ,
, 与曲面
与曲面 围成的封闭几何体叫做球面三棱锥,记为球面
围成的封闭几何体叫做球面三棱锥,记为球面 .设
.设 ,
,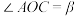 ,
,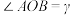 ,则下列结论正确的是( )
,则下列结论正确的是( )
 的半径为
的半径为 ,
, ,
, ,
, 为球面上三点,劣弧
为球面上三点,劣弧 的弧长记为
的弧长记为 ,设
,设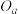 表示以
表示以 为圆心,且过
为圆心,且过 ,
, 的圆,同理,圆
的圆,同理,圆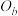 ,
, 的劣弧
的劣弧 ,
, 的弧长分别记为
的弧长分别记为 ,
, ,曲面
,曲面 (阴影部分)叫做曲面三角形,若
(阴影部分)叫做曲面三角形,若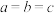 ,则称其为曲面等边三角形,线段
,则称其为曲面等边三角形,线段 ,
, ,
, 与曲面
与曲面 围成的封闭几何体叫做球面三棱锥,记为球面
围成的封闭几何体叫做球面三棱锥,记为球面 .设
.设 ,
,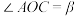 ,
,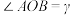 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.若平面 是面积为 是面积为 的等边三角形,则 的等边三角形,则 |
B.若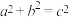 ,则 ,则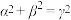 |
C.若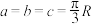 ,则球面 ,则球面 的体积 的体积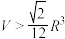 |
D.若平面 为直角三角形,且 为直角三角形,且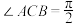 ,则 ,则 |
您最近一年使用:0次
2024-02-23更新
|
1018次组卷
|
5卷引用:贵州省贵阳市清华中学2023-2024学年高二下学期4月月考数学试题
名校
解题方法
2 . “圆锥容球”是指圆锥形容器里放了一个球,且球与圆锥的侧面及底面均相切(即圆锥的内切球).已知某圆锥形容器的母线与底面所成的角为 ,底面半径为2,则该圆锥内切球的表面积为
,底面半径为2,则该圆锥内切球的表面积为______ .(容器壁的厚度忽略不计)
 ,底面半径为2,则该圆锥内切球的表面积为
,底面半径为2,则该圆锥内切球的表面积为
您最近一年使用:0次
3 . 声强级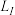 (单位:
(单位: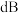 )由公式
)由公式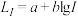 给出,其中
给出,其中 为声强(单位:
为声强(单位: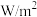 ),不同声的声强级如下,则( )
),不同声的声强级如下,则( )
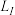 (单位:
(单位: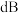 )由公式
)由公式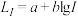 给出,其中
给出,其中 为声强(单位:
为声强(单位: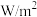 ),不同声的声强级如下,则( )
),不同声的声强级如下,则( ) ( ( ) ) | 正常人能忍受最高声强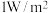 | 正常人能忍受最低声强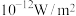 | 正常人平时谈话声强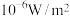 | 某人谈话声强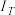 |
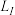 ( (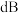 ) ) | 120 | 0 | 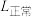 | 80 |
A.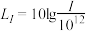 | B.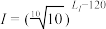 | C. | D. |
您最近一年使用:0次
解题方法
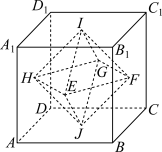
4 . 如图点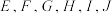 分别是棱长为2的正方体
分别是棱长为2的正方体 六个面的中心,以
六个面的中心,以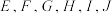 为顶点的多面体记为八面体
为顶点的多面体记为八面体 ,则( )
,则( )
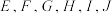 分别是棱长为2的正方体
分别是棱长为2的正方体 六个面的中心,以
六个面的中心,以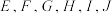 为顶点的多面体记为八面体
为顶点的多面体记为八面体 ,则( )
,则( )
A.四点 共面 共面 | B.八面体 的外接球表面积为 的外接球表面积为 |
C.八面体 的体积为 的体积为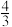 | D.直线 与八面体 与八面体 的各面所成的角都是 的各面所成的角都是 |
您最近一年使用:0次
解题方法
5 . 定义域为 的函数
的函数 满足
满足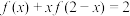 ,直线
,直线 :
: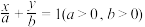 与两坐标轴分别交于
与两坐标轴分别交于 、
、 两点,则( )
两点,则( )
 的函数
的函数 满足
满足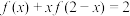 ,直线
,直线 :
: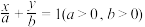 与两坐标轴分别交于
与两坐标轴分别交于 、
、 两点,则( )
两点,则( )A. |
B. 的图象关于点 的图象关于点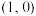 对称 对称 |
C.当直线 与 与 的图象有三个交点时,三角形 的图象有三个交点时,三角形 面积的最小值为2 面积的最小值为2 |
D.函数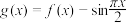 在区间 在区间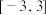 上有3个零点 上有3个零点 |
您最近一年使用:0次
6 . 函数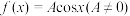 的图象向右平移
的图象向右平移 (其中
(其中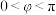 )个单位得到曲线
)个单位得到曲线 ,若
,若 在
在 处的切线方程是
处的切线方程是 ,则曲线
,则曲线 的一条对称轴方程为
的一条对称轴方程为______ .
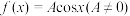 的图象向右平移
的图象向右平移 (其中
(其中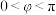 )个单位得到曲线
)个单位得到曲线 ,若
,若 在
在 处的切线方程是
处的切线方程是 ,则曲线
,则曲线 的一条对称轴方程为
的一条对称轴方程为
您最近一年使用:0次
7 . 圆 :
: 与
与 轴的负半轴和正半轴分别交于
轴的负半轴和正半轴分别交于 两点,
两点, 是圆与
是圆与 轴垂直非直径的弦,直线
轴垂直非直径的弦,直线 与直线
与直线 交于点
交于点 ,记动点
,记动点 的轨迹为
的轨迹为 .
.
(1)求轨迹 的方程;
的方程;
(2)在平面直角坐标系中,倾斜角确定的直线称为定向直线.是否存在不过点 的定向直线
的定向直线 ,当直线
,当直线 与轨迹
与轨迹 交于
交于 时,
时, ;若存在,求直线
;若存在,求直线 的一个方向向量;若不存在,说明理由.
的一个方向向量;若不存在,说明理由.
 :
: 与
与 轴的负半轴和正半轴分别交于
轴的负半轴和正半轴分别交于 两点,
两点, 是圆与
是圆与 轴垂直非直径的弦,直线
轴垂直非直径的弦,直线 与直线
与直线 交于点
交于点 ,记动点
,记动点 的轨迹为
的轨迹为 .
.(1)求轨迹
 的方程;
的方程;(2)在平面直角坐标系中,倾斜角确定的直线称为定向直线.是否存在不过点
 的定向直线
的定向直线 ,当直线
,当直线 与轨迹
与轨迹 交于
交于 时,
时, ;若存在,求直线
;若存在,求直线 的一个方向向量;若不存在,说明理由.
的一个方向向量;若不存在,说明理由.
您最近一年使用:0次
2023-11-24更新
|
561次组卷
|
5卷引用:贵州省贵阳市2024届高三上学期期中质量监测数学试卷
贵州省贵阳市2024届高三上学期期中质量监测数学试卷河南省郑州市宇华实验学校2024届高三上学期12月月考数学试题江西省南昌市2023-2024学年高二上学期期末模拟数学试题(已下线)专题03 圆锥曲线的方程(2)(已下线)大招2 动点问题处理策略(解题大招)
解题方法
8 . 阅读材料:
在平面直角坐标系中,若点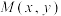 与定点
与定点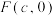 (或
(或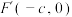 的距离和它到定直线
的距离和它到定直线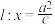 (或
(或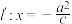 )的距离之比是常数
)的距离之比是常数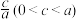 ,则
,则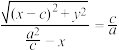 ,化简可得
,化简可得 ,设
,设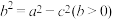 ,则得到方程
,则得到方程 ,所以点
,所以点 的轨迹是一个椭圆,这是从另一个角度给出了椭圆的定义.这里定点
的轨迹是一个椭圆,这是从另一个角度给出了椭圆的定义.这里定点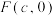 是椭圆的一个焦点,直线
是椭圆的一个焦点,直线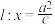 称为相应于焦点
称为相应于焦点 的准线;定点
的准线;定点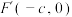 是椭圆的另一个焦点,直线
是椭圆的另一个焦点,直线 称为相应于焦点
称为相应于焦点 的准线.
的准线.
根据椭圆的这个定义,我们可以把到焦点的距离转化为到准线的距离.若点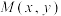 在椭圆
在椭圆 上,
上,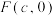 是椭圆的右焦点,椭圆的离心率
是椭圆的右焦点,椭圆的离心率 ,则点
,则点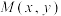 到准线
到准线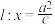 的距离为
的距离为 ,所以
,所以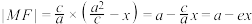 ,我们把这个公式称为椭圆的焦半径公式.
,我们把这个公式称为椭圆的焦半径公式.
结合阅读材料回答下面的问题:
已知椭圆 的右焦点为
的右焦点为 ,点
,点 是该椭圆上第一象限的点,且
是该椭圆上第一象限的点,且 轴,若直线
轴,若直线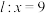 是椭圆右准线方程,点
是椭圆右准线方程,点 到直线
到直线 的距离为8.
的距离为8.
(1)求点 的坐标;
的坐标;
(2)若点 也在椭圆
也在椭圆 上且
上且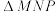 的重心为
的重心为 ,判断
,判断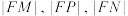 是否能构成等差数列?如果能,求出该等差数列的公差,如果不能,说明理由.
是否能构成等差数列?如果能,求出该等差数列的公差,如果不能,说明理由.
在平面直角坐标系中,若点
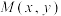 与定点
与定点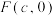 (或
(或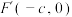 的距离和它到定直线
的距离和它到定直线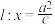 (或
(或 )的距离之比是常数
)的距离之比是常数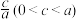 ,则
,则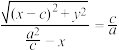 ,化简可得
,化简可得 ,设
,设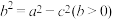 ,则得到方程
,则得到方程 ,所以点
,所以点 的轨迹是一个椭圆,这是从另一个角度给出了椭圆的定义.这里定点
的轨迹是一个椭圆,这是从另一个角度给出了椭圆的定义.这里定点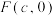 是椭圆的一个焦点,直线
是椭圆的一个焦点,直线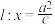 称为相应于焦点
称为相应于焦点 的准线;定点
的准线;定点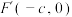 是椭圆的另一个焦点,直线
是椭圆的另一个焦点,直线 称为相应于焦点
称为相应于焦点 的准线.
的准线.根据椭圆的这个定义,我们可以把到焦点的距离转化为到准线的距离.若点
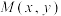 在椭圆
在椭圆 上,
上,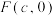 是椭圆的右焦点,椭圆的离心率
是椭圆的右焦点,椭圆的离心率 ,则点
,则点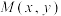 到准线
到准线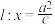 的距离为
的距离为 ,所以
,所以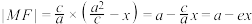 ,我们把这个公式称为椭圆的焦半径公式.
,我们把这个公式称为椭圆的焦半径公式.结合阅读材料回答下面的问题:
已知椭圆
 的右焦点为
的右焦点为 ,点
,点 是该椭圆上第一象限的点,且
是该椭圆上第一象限的点,且 轴,若直线
轴,若直线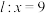 是椭圆右准线方程,点
是椭圆右准线方程,点 到直线
到直线 的距离为8.
的距离为8.(1)求点
 的坐标;
的坐标;(2)若点
 也在椭圆
也在椭圆 上且
上且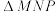 的重心为
的重心为 ,判断
,判断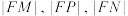 是否能构成等差数列?如果能,求出该等差数列的公差,如果不能,说明理由.
是否能构成等差数列?如果能,求出该等差数列的公差,如果不能,说明理由.
您最近一年使用:0次
9 . 下列运算结果正确的是( )
A.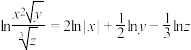 | B. |
C.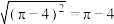 | D.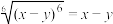 |
您最近一年使用:0次
名校
解题方法
10 . 请阅读下列材料,并解决问题: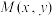 到一个定点
到一个定点 的距离和
的距离和 到定直线
到定直线 的距离的比是常数
的距离的比是常数 ,则动点的轨迹就是圆锥曲线(这个圆锥曲线的第二定义).其中定点
,则动点的轨迹就是圆锥曲线(这个圆锥曲线的第二定义).其中定点 称为其焦点,定直线
称为其焦点,定直线 称为其准线(其中椭圆与双曲线的准线方程为
称为其准线(其中椭圆与双曲线的准线方程为 ,抛物线准线方程为
,抛物线准线方程为 ),正常数
),正常数 称为其离心率.当
称为其离心率.当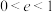 时,轨迹为椭圆;当
时,轨迹为椭圆;当 时,轨迹为抛物线;当
时,轨迹为抛物线;当 时,轨迹为双曲线.
时,轨迹为双曲线.
(1)已知平面内的动点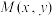 到一个定点
到一个定点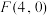 的距离和
的距离和 到定直线
到定直线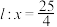 的距离的比是常数
的距离的比是常数 ,则动点
,则动点 的轨迹方程为 (直接写出结果,无需过程).
的轨迹方程为 (直接写出结果,无需过程).
(2)在(1)所求的曲线中是否存在一点,使得该点到直线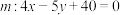 的距离最小?最小距离是多少?
的距离最小?最小距离是多少?
圆锥曲线的第二定义
二次曲线,即圆锥曲线,是由一平面截二次锥面得到的曲线,包括椭圆,抛物线,双曲线等.2000多年前,古希腊数学家最先开始研究二次曲线,并获得了大量的成果.古希腊数学家阿波罗尼斯采用平面切割圆锥的方法来研究二次曲线.阿波罗尼斯曾把椭圆叫“亏曲线”把双曲线叫做“超曲线”,把抛物线叫做“齐曲线”,事实上,二次曲线由很多统一的定义、统一的二级结论等等.比如:平面内的动点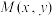 到一个定点
到一个定点 的距离和
的距离和 到定直线
到定直线 的距离的比是常数
的距离的比是常数 ,则动点的轨迹就是圆锥曲线(这个圆锥曲线的第二定义).其中定点
,则动点的轨迹就是圆锥曲线(这个圆锥曲线的第二定义).其中定点 称为其焦点,定直线
称为其焦点,定直线 称为其准线(其中椭圆与双曲线的准线方程为
称为其准线(其中椭圆与双曲线的准线方程为 ,抛物线准线方程为
,抛物线准线方程为 ),正常数
),正常数 称为其离心率.当
称为其离心率.当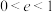 时,轨迹为椭圆;当
时,轨迹为椭圆;当 时,轨迹为抛物线;当
时,轨迹为抛物线;当 时,轨迹为双曲线.
时,轨迹为双曲线.(1)已知平面内的动点
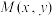 到一个定点
到一个定点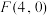 的距离和
的距离和 到定直线
到定直线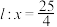 的距离的比是常数
的距离的比是常数 ,则动点
,则动点 的轨迹方程为 (直接写出结果,无需过程).
的轨迹方程为 (直接写出结果,无需过程).(2)在(1)所求的曲线中是否存在一点,使得该点到直线
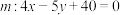 的距离最小?最小距离是多少?
的距离最小?最小距离是多少?
您最近一年使用:0次
2023-12-28更新
|
471次组卷
|
4卷引用:贵州省清镇市博雅实验学校2023-2024学年高二上学期第四次月考数学试题数学
贵州省清镇市博雅实验学校2023-2024学年高二上学期第四次月考数学试题数学重庆市万州二中教育集团2023-2024学年高二下学期入学质量监测数学试题(已下线)专题2 点点距离 构造函数 练(已下线)情境15 二级结论命题



