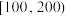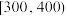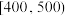名校
解题方法
1 . 甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表.
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)依据小概率值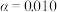 的独立性检验,分析甲机床的产品质量是否与乙机床的产品质量有差异.
的独立性检验,分析甲机床的产品质量是否与乙机床的产品质量有差异.
附:χ2=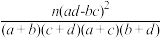 .
.
| 机床 | 品级 | 合计 | |
| 一级品 | 二级品 | ||
| 甲机床 | 150 | 50 | 200 |
| 乙机床 | 120 | 80 | 200 |
| 合计 | 270 | 130 | 400 |
(2)依据小概率值
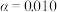 的独立性检验,分析甲机床的产品质量是否与乙机床的产品质量有差异.
的独立性检验,分析甲机床的产品质量是否与乙机床的产品质量有差异.附:χ2=
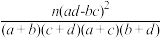 .
.| α | 0.050 | 0.010 | 0.001 |
| xα | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
解题方法
2 . 某大学生参加社会实践活动,对某公司 月份至
月份至 月份销售某种配件的销售量及销售单价进行了调查,销售单价
月份销售某种配件的销售量及销售单价进行了调查,销售单价 和销售量
和销售量 之间的一组数据如下表所示:
之间的一组数据如下表所示:
(1)根据 至
至 月份的数据,求出
月份的数据,求出 关于
关于 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过 元,则认为所得到的回归直线方程是理想的,试问
元,则认为所得到的回归直线方程是理想的,试问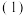 中所得到的回归直线方程是否理想?
中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从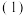 中的关系,若该种机器配件的成本是
中的关系,若该种机器配件的成本是 元
元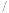 件,那么该配件的销售单价应定为多少元才能获得最大利润?
件,那么该配件的销售单价应定为多少元才能获得最大利润? 注:利润
注:利润 销售收入
销售收入 成本
成本 .
.
参考公式:回归直线方程 ,其中
,其中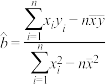 ,
,

 月份至
月份至 月份销售某种配件的销售量及销售单价进行了调查,销售单价
月份销售某种配件的销售量及销售单价进行了调查,销售单价 和销售量
和销售量 之间的一组数据如下表所示:
之间的一组数据如下表所示:| 月份 |  |  |  |  |  |  |
销售单价 元 元 | 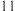 | 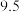 |  | 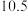 |  | 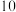 |
销售量 件 件 | 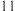 | 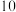 |  |  | 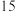 | 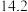 |
 至
至 月份的数据,求出
月份的数据,求出 关于
关于 的回归直线方程;
的回归直线方程;(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过
 元,则认为所得到的回归直线方程是理想的,试问
元,则认为所得到的回归直线方程是理想的,试问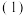 中所得到的回归直线方程是否理想?
中所得到的回归直线方程是否理想?(3)预计在今后的销售中,销售量与销售单价仍然服从
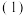 中的关系,若该种机器配件的成本是
中的关系,若该种机器配件的成本是 元
元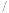 件,那么该配件的销售单价应定为多少元才能获得最大利润?
件,那么该配件的销售单价应定为多少元才能获得最大利润? 注:利润
注:利润 销售收入
销售收入 成本
成本 .
.参考公式:回归直线方程
 ,其中
,其中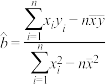 ,
,
您最近一年使用:0次
名校
3 . 某企业为响应国家节水号召,决定对污水进行净化再利用,以降低自来水的使用量.经测算,企业拟安装一种使用寿命为4年的污水净化设备.这种净水设备的购置费(单位:万元)与设备的占地面积 (单位:平方米)成正比,比例系数为0.2,预计安装后该企业每年需缴纳的水费
(单位:平方米)成正比,比例系数为0.2,预计安装后该企业每年需缴纳的水费 (单位:万元)与设备占地面积
(单位:万元)与设备占地面积 之间的函数关系为
之间的函数关系为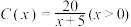 ,将该企业的净水设备购置费与安装后4年需缴水费之和合计为
,将该企业的净水设备购置费与安装后4年需缴水费之和合计为 (单位:万元).
(单位:万元).
(1)要使 不超过7.2万元,求设备占地面积
不超过7.2万元,求设备占地面积 的取值范围;
的取值范围;
(2)设备占地面积 为多少时,
为多少时, 的值最小?
的值最小?
 (单位:平方米)成正比,比例系数为0.2,预计安装后该企业每年需缴纳的水费
(单位:平方米)成正比,比例系数为0.2,预计安装后该企业每年需缴纳的水费 (单位:万元)与设备占地面积
(单位:万元)与设备占地面积 之间的函数关系为
之间的函数关系为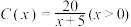 ,将该企业的净水设备购置费与安装后4年需缴水费之和合计为
,将该企业的净水设备购置费与安装后4年需缴水费之和合计为 (单位:万元).
(单位:万元).(1)要使
 不超过7.2万元,求设备占地面积
不超过7.2万元,求设备占地面积 的取值范围;
的取值范围;(2)设备占地面积
 为多少时,
为多少时, 的值最小?
的值最小?
您最近一年使用:0次
2024-09-13更新
|
1057次组卷
|
7卷引用:广东省中山市华侨中学2025届高三第一次模拟考试数学试题
名校
4 . 已知函数 的图象过点
的图象过点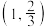 ,且
,且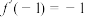 .
.
(1)求 ,
, 的值;
的值;
(2)求函数 的极值.
的极值.
 的图象过点
的图象过点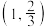 ,且
,且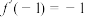 .
.(1)求
 ,
, 的值;
的值;(2)求函数
 的极值.
的极值.
您最近一年使用:0次
2024-08-06更新
|
1085次组卷
|
3卷引用:2025届甘肃省武威市凉州区高三一模数学试卷
解题方法
5 . 已知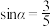 ,
, 是第二象限角.
是第二象限角.
(1)求 和
和 的值;
的值;
(2)求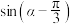 的值.
的值.
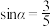 ,
, 是第二象限角.
是第二象限角.(1)求
 和
和 的值;
的值;(2)求
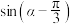 的值.
的值.
您最近一年使用:0次
名校
解题方法
6 . 已知数列 为公差不为零的等差数列,其前n项和为
为公差不为零的等差数列,其前n项和为 ,
, ,且
,且 ,
, ,
,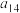 成等比数列.
成等比数列.
(1)求 的通项公式;
的通项公式;
(2)若数列 是公比为3的等比数列,且
是公比为3的等比数列,且 ,求
,求 的前n项和
的前n项和 .
.
 为公差不为零的等差数列,其前n项和为
为公差不为零的等差数列,其前n项和为 ,
, ,且
,且 ,
, ,
,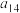 成等比数列.
成等比数列.(1)求
 的通项公式;
的通项公式;(2)若数列
 是公比为3的等比数列,且
是公比为3的等比数列,且 ,求
,求 的前n项和
的前n项和 .
.
您最近一年使用:0次
2024-07-05更新
|
2252次组卷
|
7卷引用:浙江省县城教研联盟2023-2024学年高三下学期模拟考试数学试题
名校
7 . 等比数列 中,
中, ,
, .
.
(1)求 的通项公式:
的通项公式:
(2)记 为
为 的前n项和,若
的前n项和,若 ,求m.
,求m.
 中,
中, ,
, .
.(1)求
 的通项公式:
的通项公式:(2)记
 为
为 的前n项和,若
的前n项和,若 ,求m.
,求m.
您最近一年使用:0次
2024-06-14更新
|
332次组卷
|
2卷引用:四川省遂宁市射洪中学校2024届高三下学期三模理科数学试题
名校
8 . 某体育学校为储备人才,准备通过测试(按照测试成绩高分优先录取的原则)录用学生300人,其中测试成绩前100名的学生为第一梯队,剩余的200名学生为第二梯队.实际报名学生为1000人,测试满分为100分.测试后,对学生的测试成绩进行了抽样分析,得到如图所示的频率分布直方图.
(2)试估计该学校本次测试的录取分数,并判断测试成绩为88分的学生甲能否被录取?若能被录取,能否进入第一梯队?

(2)试估计该学校本次测试的录取分数,并判断测试成绩为88分的学生甲能否被录取?若能被录取,能否进入第一梯队?
您最近一年使用:0次
2024-06-08更新
|
317次组卷
|
2卷引用:2024届山东省实验中学高三下学期5月高考模拟数学试题
9 . 随着网络技术的迅速发展,各种购物群成为网络销售的新渠道.2023年11月某地脐橙开始采摘上市,一脐橙基地随机抽查了100个购物群的销售情况,各购物群销售脐橙的情况如下:
(1)求实数 的值.并用组中值(每组的中点值)估计这100个购物群销售脐橙总量的平均数;
的值.并用组中值(每组的中点值)估计这100个购物群销售脐橙总量的平均数;
(2)假设所有购物群销售脐橙的数量 ,其中
,其中 为(1)中的平均数,
为(1)中的平均数,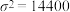 .若该脐橙基地参与销售的购物群约有1000个,销售的脐橙在
.若该脐橙基地参与销售的购物群约有1000个,销售的脐橙在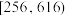 (单位:盒)内的群为“
(单位:盒)内的群为“ 级群”,销售数量小于256盒的购物群为“
级群”,销售数量小于256盒的购物群为“ 级群”,销售数量不小于616盒的购物群为“特级群”,该脐橙基地对每个“特级群”奖励600元,每个“
级群”,销售数量不小于616盒的购物群为“特级群”,该脐橙基地对每个“特级群”奖励600元,每个“ 级群”奖励100,对“
级群”奖励100,对“ 级群”不奖励,则该脐橙基地大约需要准备多少奖金?(群的个数按四舍五入取整数)
级群”不奖励,则该脐橙基地大约需要准备多少奖金?(群的个数按四舍五入取整数)
附:若 ,则
,则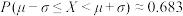 ,
,
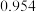 ,
, .
.
脐橙数量/盒 |
|
|
|
|
|
购物群数量/个 | 12 | 18 |
| 32 | 18 |
 的值.并用组中值(每组的中点值)估计这100个购物群销售脐橙总量的平均数;
的值.并用组中值(每组的中点值)估计这100个购物群销售脐橙总量的平均数;(2)假设所有购物群销售脐橙的数量
 ,其中
,其中 为(1)中的平均数,
为(1)中的平均数,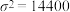 .若该脐橙基地参与销售的购物群约有1000个,销售的脐橙在
.若该脐橙基地参与销售的购物群约有1000个,销售的脐橙在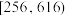 (单位:盒)内的群为“
(单位:盒)内的群为“ 级群”,销售数量小于256盒的购物群为“
级群”,销售数量小于256盒的购物群为“ 级群”,销售数量不小于616盒的购物群为“特级群”,该脐橙基地对每个“特级群”奖励600元,每个“
级群”,销售数量不小于616盒的购物群为“特级群”,该脐橙基地对每个“特级群”奖励600元,每个“ 级群”奖励100,对“
级群”奖励100,对“ 级群”不奖励,则该脐橙基地大约需要准备多少奖金?(群的个数按四舍五入取整数)
级群”不奖励,则该脐橙基地大约需要准备多少奖金?(群的个数按四舍五入取整数)附:若
 ,则
,则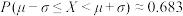 ,
,
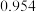 ,
, .
.
您最近一年使用:0次
2024-06-07更新
|
338次组卷
|
5卷引用:陕西省商洛市柞水中学2024届高三下学期高考模拟预测理科数学试题
陕西省商洛市柞水中学2024届高三下学期高考模拟预测理科数学试题(已下线)【高二模块二】类型3 以随机变量及其分布为背景的解答题(A卷基础卷)湖南省益阳市安化县两校联考2023-2024学年高二下学期7月期末自检数学试题湖南省永州市名校联盟2023-2024学年高二下学期期末考试数学试题(已下线)7.4 常见的几种分布列
名校
解题方法
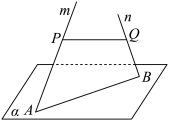
10 . 如图,空间中有一个平面 和两条互相垂直的异面直线
和两条互相垂直的异面直线 、
、 ,其中
,其中 、
、 与
与 的交点分别为
的交点分别为 ,直线
,直线 、
、 都与直线
都与直线 垂直,垂足分别为
垂直,垂足分别为 、
、 ,且
,且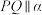 .
. 、
、 与平面
与平面 所成角之和为定值;
所成角之和为定值;
(2)若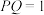 ,令
,令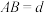 (
( ),求点
),求点 到平面
到平面 距离的最大值关于
距离的最大值关于 的函数
的函数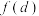 .
.
 和两条互相垂直的异面直线
和两条互相垂直的异面直线 、
、 ,其中
,其中 、
、 与
与 的交点分别为
的交点分别为 ,直线
,直线 、
、 都与直线
都与直线 垂直,垂足分别为
垂直,垂足分别为 、
、 ,且
,且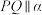 .
.
 、
、 与平面
与平面 所成角之和为定值;
所成角之和为定值;(2)若
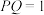 ,令
,令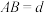 (
( ),求点
),求点 到平面
到平面 距离的最大值关于
距离的最大值关于 的函数
的函数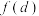 .
.
您最近一年使用:0次