名校
解题方法
1 . 已知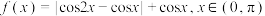 ,下列四种说法
,下列四种说法
① 在
在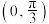 上单调递增;
上单调递增;
② 在
在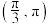 上单调递减;
上单调递减;
③ 的值域为
的值域为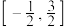 ;
;
④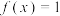 的根有且只有一个.
的根有且只有一个.
其中正确说法的序号为__________ .
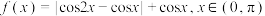 ,下列四种说法
,下列四种说法①
 在
在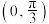 上单调递增;
上单调递增; ②
 在
在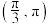 上单调递减;
上单调递减; ③
 的值域为
的值域为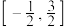 ;
; ④
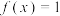 的根有且只有一个.
的根有且只有一个.其中正确说法的序号为
您最近一年使用:0次
2 . 声音是由物体振动产生的声波,其中包含着正弦函数,纯音的数学模型是函数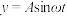 ,我们听到的声音是由纯音合成的,称之为复合音,若一个复合音的数学模型是函数
,我们听到的声音是由纯音合成的,称之为复合音,若一个复合音的数学模型是函数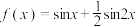 ,给出下列结论:
,给出下列结论:
① 的图象关于直线
的图象关于直线 对称; ②
对称; ② 在
在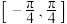 上是增函数;
上是增函数;
③ 的最大值为
的最大值为 ; ④
; ④ 的图象关于
的图象关于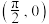 对称
对称
其中正确说法的序号为______ .
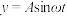 ,我们听到的声音是由纯音合成的,称之为复合音,若一个复合音的数学模型是函数
,我们听到的声音是由纯音合成的,称之为复合音,若一个复合音的数学模型是函数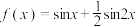 ,给出下列结论:
,给出下列结论:①
 的图象关于直线
的图象关于直线 对称; ②
对称; ② 在
在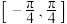 上是增函数;
上是增函数;③
 的最大值为
的最大值为 ; ④
; ④ 的图象关于
的图象关于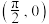 对称
对称其中正确说法的序号为
您最近一年使用:0次
名校
解题方法
3 . 对下列命题:
(1)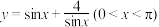 的最小值为4;
的最小值为4;
(2)若 是各项均为正数的等比数列,则
是各项均为正数的等比数列,则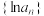 是等差数列;
是等差数列;
(3)已知 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,
, ,
, ,且最大边长为
,且最大边长为 ,若
,若 ,则
,则 一定是锐角三角形;
一定是锐角三角形;
其中所有正确命题的序号为_________ (填出所有正确命题的序号).
(1)
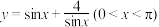 的最小值为4;
的最小值为4;(2)若
 是各项均为正数的等比数列,则
是各项均为正数的等比数列,则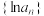 是等差数列;
是等差数列;(3)已知
 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,
, ,
, ,且最大边长为
,且最大边长为 ,若
,若 ,则
,则 一定是锐角三角形;
一定是锐角三角形;其中所有正确命题的序号为
您最近一年使用:0次
4 . 对下列命题:
(1) 的最小值为4;
的最小值为4;
(2)若 是各项均为正数的等比数列,则
是各项均为正数的等比数列,则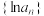 是等差数列;
是等差数列;
(3)已知 的三个内角
的三个内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, 且最大边长为
且最大边长为 ,若
,若 ,则
,则 一定是锐角三角形;
一定是锐角三角形;
(4)若向量 ,
,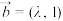 ,且
,且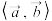 是锐角,则实数的取值范围为
是锐角,则实数的取值范围为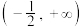 ;
;
其中所有正确命题的序号为_________ (填出所有正确命题的序号).
(1)
 的最小值为4;
的最小值为4;(2)若
 是各项均为正数的等比数列,则
是各项均为正数的等比数列,则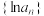 是等差数列;
是等差数列;(3)已知
 的三个内角
的三个内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, 且最大边长为
且最大边长为 ,若
,若 ,则
,则 一定是锐角三角形;
一定是锐角三角形;(4)若向量
 ,
,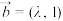 ,且
,且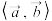 是锐角,则实数的取值范围为
是锐角,则实数的取值范围为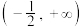 ;
;其中所有正确命题的序号为
您最近一年使用:0次
2020-07-25更新
|
510次组卷
|
2卷引用:四川省眉山市2019-2020学年高一下学期期末考试数学试题
名校
5 . 给出以下命题:
①若α、β是第一象限角且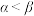 ,则
,则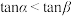 ;
;
②函数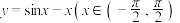 有三个零点;
有三个零点;
③函数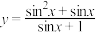 是奇函数;
是奇函数;
④函数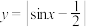 的周期是
的周期是 ;
;
⑤函数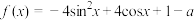 ,当
,当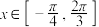 时
时 恒有解,则a的范围是
恒有解,则a的范围是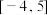 .
.
其中正确命题的序号为____________ .
①若α、β是第一象限角且
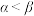 ,则
,则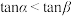 ;
;②函数
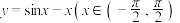 有三个零点;
有三个零点;③函数
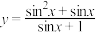 是奇函数;
是奇函数;④函数
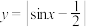 的周期是
的周期是 ;
;⑤函数
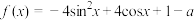 ,当
,当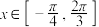 时
时 恒有解,则a的范围是
恒有解,则a的范围是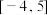 .
.其中正确命题的序号为
您最近一年使用:0次
2020-02-29更新
|
1423次组卷
|
6卷引用:四川省泸县第一中学2022-2023学年高一下学期期中数学试题
四川省泸县第一中学2022-2023学年高一下学期期中数学试题安徽省六安市第一中学2018-2019学年高一下学期第一次段考数学(理)试题(已下线)专题02 三角函数 三角恒等变换(难点)-2020-2021学年高一数学下学期期末专项复习(北师大版2019必修第二册)(已下线)专题5.10 三角函数综合应用-《聚能闯关》2021-2022学年高一数学提优闯关训练(人教A版2019必修第一册)(已下线)专题5综合闯关 (提升版)(已下线)专题09 三角恒等变换、函数y=Asin(ωx+φ)及三角函数应用2-期末复习重难培优与单元检测(人教A版2019)
名校
6 . 给出以下四个命题:
①若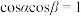 ,则
,则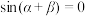 ;
;
②已知直线 与函数
与函数 ,
, 的图像分别交于点
的图像分别交于点 ,则
,则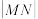 的最大值为
的最大值为 ;
;
③若数列 为单调递增数列,则
为单调递增数列,则 取值范围是
取值范围是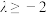 ;
;
④已知数列 的通项
的通项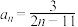 ,前
,前 项和为
项和为 ,则使
,则使 的
的 的最小值为12.
的最小值为12.
其中正确命题的序号为__________ .
①若
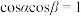 ,则
,则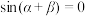 ;
;②已知直线
 与函数
与函数 ,
, 的图像分别交于点
的图像分别交于点 ,则
,则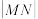 的最大值为
的最大值为 ;
;③若数列
 为单调递增数列,则
为单调递增数列,则 取值范围是
取值范围是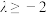 ;
;④已知数列
 的通项
的通项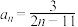 ,前
,前 项和为
项和为 ,则使
,则使 的
的 的最小值为12.
的最小值为12.其中正确命题的序号为
您最近一年使用:0次
2020-05-22更新
|
797次组卷
|
3卷引用:四川省宜宾市叙州区第二中学校2020-2021学年高三上学期开学考试数学(理)试题
名校
7 . 给出以下几个结论:
①若 ,
, ,则
,则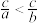 ;
;
②如果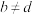 且
且 都不为
都不为 ,则
,则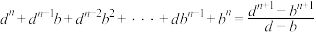 ,
, ;
;
③若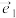 ,
,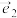 是夹角为
是夹角为 的两个单位向量,则
的两个单位向量,则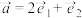 ,
,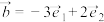 的夹角为
的夹角为 ;
;
④在 中,三内角
中,三内角 所对的边分别为
所对的边分别为 ,则
,则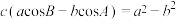 ;
;
其中正确结论的序号为______ .
①若
 ,
, ,则
,则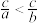 ;
;②如果
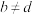 且
且 都不为
都不为 ,则
,则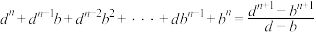 ,
, ;
;③若
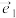 ,
,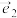 是夹角为
是夹角为 的两个单位向量,则
的两个单位向量,则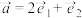 ,
,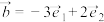 的夹角为
的夹角为 ;
;④在
 中,三内角
中,三内角 所对的边分别为
所对的边分别为 ,则
,则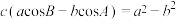 ;
;其中正确结论的序号为
您最近一年使用:0次
2020-05-15更新
|
412次组卷
|
2卷引用:四川省眉山市2018-2019学年高一下学期期末数学试题
名校
8 . 给出下列命题:
①函数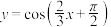 是奇函数;
是奇函数;
②存在实数 ,使
,使 ;
;
③若 ,
, 是第一象限角且
是第一象限角且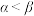 ,则
,则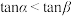 ;
;
④函数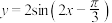 在
在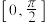 上的值域为
上的值域为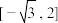 ;
;
⑤函数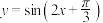 的图象关于点
的图象关于点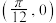 成中心对称.其中正确命题的序号为
成中心对称.其中正确命题的序号为_________ .
①函数
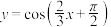 是奇函数;
是奇函数;②存在实数
 ,使
,使 ;
;③若
 ,
, 是第一象限角且
是第一象限角且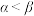 ,则
,则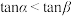 ;
;④函数
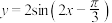 在
在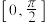 上的值域为
上的值域为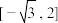 ;
;⑤函数
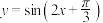 的图象关于点
的图象关于点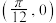 成中心对称.其中正确命题的序号为
成中心对称.其中正确命题的序号为
您最近一年使用:0次
2020-02-20更新
|
317次组卷
|
2卷引用:四川省泸州市泸县第五中学2019-2020学年高一下学期期中考试数学试题
13-14高三上·广东揭阳·期中
名校
解题方法
9 . 已知函数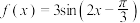 的图象为
的图象为 ,则下列说法:
,则下列说法:
①图象 关于点
关于点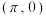 对称;
对称;
②图象 关于直线
关于直线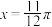 对称;
对称;
③函数 在区间
在区间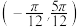 内是增函数;
内是增函数;
④由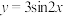 的图象向左平移
的图象向左平移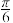 个单位长度可以得到图象
个单位长度可以得到图象 .其中正确的说法的序号为
.其中正确的说法的序号为_______ .
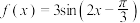 的图象为
的图象为 ,则下列说法:
,则下列说法:①图象
 关于点
关于点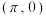 对称;
对称;②图象
 关于直线
关于直线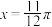 对称;
对称;③函数
 在区间
在区间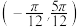 内是增函数;
内是增函数;④由
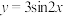 的图象向左平移
的图象向左平移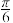 个单位长度可以得到图象
个单位长度可以得到图象 .其中正确的说法的序号为
.其中正确的说法的序号为
您最近一年使用:0次
2016-12-02更新
|
1397次组卷
|
3卷引用:四川省宜宾市叙州区第二中学校2020-2021学年高二上学期开学考试数学(文)试题
四川省宜宾市叙州区第二中学校2020-2021学年高二上学期开学考试数学(文)试题(已下线)2014届广东揭阳一中、潮州金山中学高三上学期期中联考文数学试卷山西省临汾市洪洞县第一中学2020届高三上学期期中数学(理)试题
名校
10 . 已知函数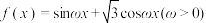 ,则下列说法正确的是
,则下列说法正确的是__________ .(填写所有正确说法的序号)
①当 时,函数
时,函数 与函数
与函数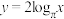 的图象有且只有一个交点.
的图象有且只有一个交点.
②当 时,且函数
时,且函数 为奇函数,则正数
为奇函数,则正数 的最小值为
的最小值为 .
.
③若函数 在
在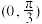 上单调递增,则
上单调递增,则 的最小值为
的最小值为 .
.
④若函数 在
在 上恰有两个极大值点,则
上恰有两个极大值点,则 的取值范围是
的取值范围是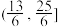 .
.
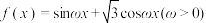 ,则下列说法正确的是
,则下列说法正确的是①当
 时,函数
时,函数 与函数
与函数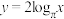 的图象有且只有一个交点.
的图象有且只有一个交点.②当
 时,且函数
时,且函数 为奇函数,则正数
为奇函数,则正数 的最小值为
的最小值为 .
.③若函数
 在
在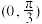 上单调递增,则
上单调递增,则 的最小值为
的最小值为 .
.④若函数
 在
在 上恰有两个极大值点,则
上恰有两个极大值点,则 的取值范围是
的取值范围是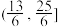 .
.
您最近一年使用:0次



