1 . 已知抛物线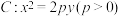 上任意一点
上任意一点 满足
满足 的最小值为
的最小值为 (
( 为焦点).
为焦点).
(1)求 的方程;
的方程;
(2)过点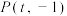 的直线经过
的直线经过 点且与物线交于
点且与物线交于 两点,求证:
两点,求证: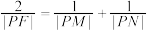 ;
;
(3)过 作一条倾斜角为
作一条倾斜角为 的直线交抛物线于
的直线交抛物线于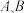 两点,过
两点,过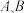 分别作抛物线的切线.两条切线交于
分别作抛物线的切线.两条切线交于 点,过
点,过 任意作一条直线交抛物线于
任意作一条直线交抛物线于 ,交直线
,交直线 于点
于点 ,则
,则 满足什么关系?并证明.
满足什么关系?并证明.
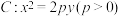 上任意一点
上任意一点 满足
满足 的最小值为
的最小值为 (
( 为焦点).
为焦点).(1)求
 的方程;
的方程;(2)过点
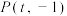 的直线经过
的直线经过 点且与物线交于
点且与物线交于 两点,求证:
两点,求证: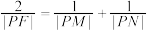 ;
;(3)过
 作一条倾斜角为
作一条倾斜角为 的直线交抛物线于
的直线交抛物线于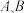 两点,过
两点,过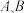 分别作抛物线的切线.两条切线交于
分别作抛物线的切线.两条切线交于 点,过
点,过 任意作一条直线交抛物线于
任意作一条直线交抛物线于 ,交直线
,交直线 于点
于点 ,则
,则 满足什么关系?并证明.
满足什么关系?并证明.
您最近一年使用:0次
2 . 已知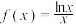 ,
,
(1)求函数 的导数,并证明:函数
的导数,并证明:函数 在
在 上是严格减函数(常数
上是严格减函数(常数 为自然对数的底);
为自然对数的底);
(2)根据(1),判断并证明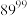 与
与 的大小关系,并请推广至一般的结论(无须证明);
的大小关系,并请推广至一般的结论(无须证明);
(3)已知 、
、 是正整数,
是正整数, ,
, ,求证:
,求证: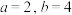 是满足条件的唯一一组值.
是满足条件的唯一一组值.
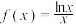 ,
,(1)求函数
 的导数,并证明:函数
的导数,并证明:函数 在
在 上是严格减函数(常数
上是严格减函数(常数 为自然对数的底);
为自然对数的底);(2)根据(1),判断并证明
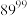 与
与 的大小关系,并请推广至一般的结论(无须证明);
的大小关系,并请推广至一般的结论(无须证明);(3)已知
 、
、 是正整数,
是正整数, ,
, ,求证:
,求证: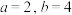 是满足条件的唯一一组值.
是满足条件的唯一一组值.
您最近一年使用:0次
2022-12-15更新
|
803次组卷
|
4卷引用:上海市嘉定区2023届高三上学期一模数学试题
3 . (1) 时,证明:
时,证明: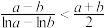 ;
;
(2)直线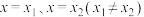 与函数
与函数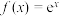 分别交于A、B两点,与函数
分别交于A、B两点,与函数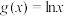 分别交于C、D两点,设直线
分别交于C、D两点,设直线 斜率为
斜率为 ,直线
,直线 斜率为
斜率为 ,求证
,求证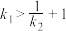 .
.
 时,证明:
时,证明: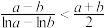 ;
;(2)直线
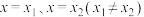 与函数
与函数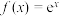 分别交于A、B两点,与函数
分别交于A、B两点,与函数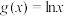 分别交于C、D两点,设直线
分别交于C、D两点,设直线 斜率为
斜率为 ,直线
,直线 斜率为
斜率为 ,求证
,求证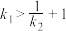 .
.
您最近一年使用:0次
4 . 设直线 ,曲线
,曲线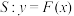 .若直线
.若直线 与曲线
与曲线 同时满足下列两个条件:①直线
同时满足下列两个条件:①直线 与曲线
与曲线 相切且至少有两个切点;②对任意
相切且至少有两个切点;②对任意 都有
都有 .则称直线
.则称直线 为曲线
为曲线 的“上夹线”.
的“上夹线”.
(1)已知函数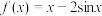 .求证:
.求证: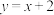 为曲线
为曲线 的“上夹线”;
的“上夹线”;
(2)观察下图: 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
 ,曲线
,曲线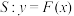 .若直线
.若直线 与曲线
与曲线 同时满足下列两个条件:①直线
同时满足下列两个条件:①直线 与曲线
与曲线 相切且至少有两个切点;②对任意
相切且至少有两个切点;②对任意 都有
都有 .则称直线
.则称直线 为曲线
为曲线 的“上夹线”.
的“上夹线”.(1)已知函数
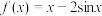 .求证:
.求证: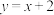 为曲线
为曲线 的“上夹线”;
的“上夹线”;(2)观察下图:

 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
您最近一年使用:0次
解题方法
5 . 已知常数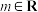 ,设
,设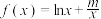 ,
,
(1)若 ,求函数
,求函数 的最小值;
的最小值;
(2)是否存在 ,且
,且 ,
, ,
, 依次成等比数列,使得
依次成等比数列,使得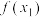 、
、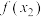 、
、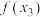 依次成等差数列?请说明理由.
依次成等差数列?请说明理由.
(3)求证:“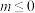 ”是“对任意
”是“对任意 ,
, ,都有
,都有 ”的充要条件.
”的充要条件.
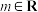 ,设
,设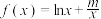 ,
,(1)若
 ,求函数
,求函数 的最小值;
的最小值;(2)是否存在
 ,且
,且 ,
, ,
, 依次成等比数列,使得
依次成等比数列,使得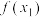 、
、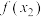 、
、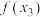 依次成等差数列?请说明理由.
依次成等差数列?请说明理由.(3)求证:“
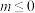 ”是“对任意
”是“对任意 ,
, ,都有
,都有 ”的充要条件.
”的充要条件.
您最近一年使用:0次
解题方法
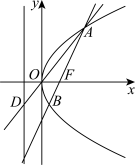
6 . 如图, 为坐标原点,
为坐标原点, 为抛物线
为抛物线 的焦点,过
的焦点,过 的直线交抛物线于
的直线交抛物线于 两点,直线
两点,直线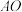 交抛物线的准线于点
交抛物线的准线于点 ,设抛物线在
,设抛物线在 点处的切线为
点处的切线为 .
. 与
与 轴的交点为
轴的交点为 ,求证:
,求证: ;
;
(2)过点 作
作 的垂线与直线
的垂线与直线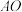 交于点
交于点 ,求证:
,求证: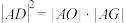 .
.
 为坐标原点,
为坐标原点, 为抛物线
为抛物线 的焦点,过
的焦点,过 的直线交抛物线于
的直线交抛物线于 两点,直线
两点,直线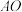 交抛物线的准线于点
交抛物线的准线于点 ,设抛物线在
,设抛物线在 点处的切线为
点处的切线为 .
.
 与
与 轴的交点为
轴的交点为 ,求证:
,求证: ;
;(2)过点
 作
作 的垂线与直线
的垂线与直线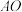 交于点
交于点 ,求证:
,求证: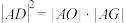 .
.
您最近一年使用:0次
2024-03-13更新
|
1553次组卷
|
4卷引用:湖北省七市州2024届高三下学期3月联合统一调研测试数学试题
湖北省七市州2024届高三下学期3月联合统一调研测试数学试题山东省潍坊市昌乐北大公学学校2024届高三下学期3月监测数学试题四川省成都市教育科学研究院附属中学2023-2024学年高三下学期4月综合测试数学(理科)试题(已下线)湖北省七市州2024届高三下学期3月联合统一调研测试数学试题变式题16-19
解题方法
7 . 拉格朗日中值定理是微分学的基本定理之一,其内容为:如果函数 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且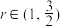 .
.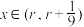 时,
时,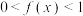 ;
;
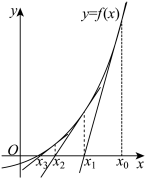
(2)从图形上看,函数 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得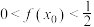 ,然后在点
,然后在点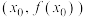 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列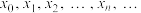 .
.
①当 时,证明:
时,证明: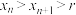 ;
;
②根据①的结论,运用数学归纳法可以证得: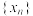 为递减数列,且
为递减数列,且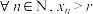 .请以此为前提条件,证明:
.请以此为前提条件,证明: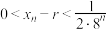 .
.
 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且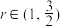 .
.
 时,
时,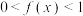 ;
;(2)从图形上看,函数
 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得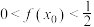 ,然后在点
,然后在点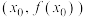 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列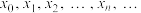 .
.①当
 时,证明:
时,证明: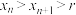 ;
;②根据①的结论,运用数学归纳法可以证得:
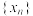 为递减数列,且
为递减数列,且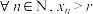 .请以此为前提条件,证明:
.请以此为前提条件,证明: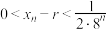 .
.
您最近一年使用:0次
8 . 已知抛物线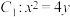 ,
,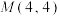 .
.
(1)直线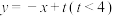 交抛物线
交抛物线 于A,B两点,求
于A,B两点,求 面积的最大值;
面积的最大值;
(2)已知P,Q是 上的不同两点,且直线的斜率
上的不同两点,且直线的斜率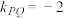 ,直线
,直线 ,
, 分别交抛物线
分别交抛物线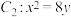 于
于 ,
,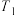 ,
, ,
, 四点,求证:
四点,求证: ,
,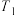 ,
, ,
, 四点共圆.
四点共圆.
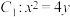 ,
,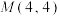 .
.(1)直线
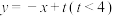 交抛物线
交抛物线 于A,B两点,求
于A,B两点,求 面积的最大值;
面积的最大值;(2)已知P,Q是
 上的不同两点,且直线的斜率
上的不同两点,且直线的斜率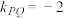 ,直线
,直线 ,
, 分别交抛物线
分别交抛物线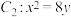 于
于 ,
,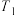 ,
, ,
, 四点,求证:
四点,求证: ,
,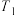 ,
, ,
, 四点共圆.
四点共圆.
您最近一年使用:0次
解题方法
9 . 记集合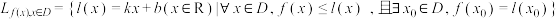 ,集合
,集合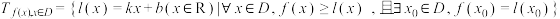 ,若
,若 ,则称直线
,则称直线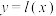 为函数
为函数 在
在 上的“最佳上界线”;若
上的“最佳上界线”;若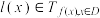 ,则称直线
,则称直线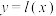 为函数
为函数 在
在 上的“最佳下界线”.
上的“最佳下界线”.
(1)已知函数 ,
, .若
.若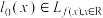 ,求
,求 的值;
的值;
(2)已知 .
.
(ⅰ)证明:直线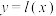 是曲线
是曲线 的一条切线的充要条件是直线
的一条切线的充要条件是直线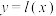 是函数
是函数 在
在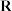 上的“最佳下界线”;
上的“最佳下界线”;
(ⅱ)若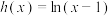 ,直接写出集合
,直接写出集合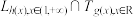 中元素的个数(无需证明).
中元素的个数(无需证明).
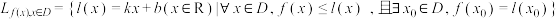 ,集合
,集合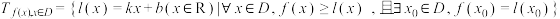 ,若
,若 ,则称直线
,则称直线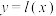 为函数
为函数 在
在 上的“最佳上界线”;若
上的“最佳上界线”;若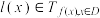 ,则称直线
,则称直线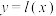 为函数
为函数 在
在 上的“最佳下界线”.
上的“最佳下界线”.(1)已知函数
 ,
, .若
.若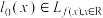 ,求
,求 的值;
的值;(2)已知
 .
.(ⅰ)证明:直线
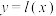 是曲线
是曲线 的一条切线的充要条件是直线
的一条切线的充要条件是直线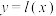 是函数
是函数 在
在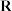 上的“最佳下界线”;
上的“最佳下界线”;(ⅱ)若
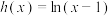 ,直接写出集合
,直接写出集合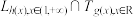 中元素的个数(无需证明).
中元素的个数(无需证明).
您最近一年使用:0次
10 . 定义:对于定义在区间 上的函数,若存在实数
上的函数,若存在实数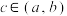 ,使得函数在区间
,使得函数在区间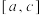 上单调递增(递减),在区间
上单调递增(递减),在区间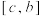 上单调递减(递增),则称这个函数为单峰函数且称
上单调递减(递增),则称这个函数为单峰函数且称 为最优点.已知定义在区间
为最优点.已知定义在区间 上的函数
上的函数 是以
是以 为最优点的单峰函数,在区间
为最优点的单峰函数,在区间 上选取关于区间的中心
上选取关于区间的中心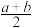 对称的两个试验点
对称的两个试验点 ,称使得
,称使得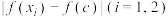 较小的试验点
较小的试验点 为好点(若相同,就任选其一),另一个称为差点.容易发现,最优点
为好点(若相同,就任选其一),另一个称为差点.容易发现,最优点 与好点在差点的同一侧.我们以差点为分界点,把区间
与好点在差点的同一侧.我们以差点为分界点,把区间 分成两部分,并称好点所在的部分为存优区间,设存优区间为
分成两部分,并称好点所在的部分为存优区间,设存优区间为 ,再对区间
,再对区间 重复以上操作,可以找到新的存优区间
重复以上操作,可以找到新的存优区间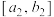 ,同理可依次找到存优区间
,同理可依次找到存优区间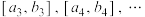 ,满足
,满足 ,可使存优区间长度逐步减小.为了方便找到最优点(或者接近最优点),从第二次操作起,将前一次操作中的好点作为本次操作的一个试验点,若每次操作后得到的存优区间长度与操作前区间的长度的比值为同一个常数
,可使存优区间长度逐步减小.为了方便找到最优点(或者接近最优点),从第二次操作起,将前一次操作中的好点作为本次操作的一个试验点,若每次操作后得到的存优区间长度与操作前区间的长度的比值为同一个常数 ,则称这样的操作是“优美的”,得到的每一个存优区间都称为优美存优区间,
,则称这样的操作是“优美的”,得到的每一个存优区间都称为优美存优区间, 称为优美存优区间常数.对区间
称为优美存优区间常数.对区间 进行
进行 次“优美的”操作,最后得到优美存优区间
次“优美的”操作,最后得到优美存优区间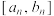 ,令
,令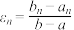 ,我们可任取区间
,我们可任取区间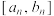 内的一个实数作为最优点
内的一个实数作为最优点 的近似值,称之为
的近似值,称之为 在区间
在区间 上精度为
上精度为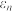 的“合规近似值”,记作
的“合规近似值”,记作 .已知函数
.已知函数 ,函数
,函数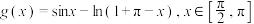 .
.
(1)求证:函数 是单峰函数;
是单峰函数;
(2)已知 为函数
为函数 的最优点,
的最优点, 为函数
为函数 的最优点.
的最优点.
(i)求证: ;
;
(ii)求证: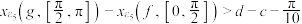 .
.
注: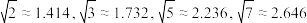 .
.
 上的函数,若存在实数
上的函数,若存在实数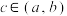 ,使得函数在区间
,使得函数在区间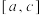 上单调递增(递减),在区间
上单调递增(递减),在区间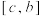 上单调递减(递增),则称这个函数为单峰函数且称
上单调递减(递增),则称这个函数为单峰函数且称 为最优点.已知定义在区间
为最优点.已知定义在区间 上的函数
上的函数 是以
是以 为最优点的单峰函数,在区间
为最优点的单峰函数,在区间 上选取关于区间的中心
上选取关于区间的中心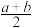 对称的两个试验点
对称的两个试验点 ,称使得
,称使得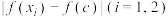 较小的试验点
较小的试验点 为好点(若相同,就任选其一),另一个称为差点.容易发现,最优点
为好点(若相同,就任选其一),另一个称为差点.容易发现,最优点 与好点在差点的同一侧.我们以差点为分界点,把区间
与好点在差点的同一侧.我们以差点为分界点,把区间 分成两部分,并称好点所在的部分为存优区间,设存优区间为
分成两部分,并称好点所在的部分为存优区间,设存优区间为 ,再对区间
,再对区间 重复以上操作,可以找到新的存优区间
重复以上操作,可以找到新的存优区间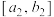 ,同理可依次找到存优区间
,同理可依次找到存优区间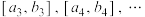 ,满足
,满足 ,可使存优区间长度逐步减小.为了方便找到最优点(或者接近最优点),从第二次操作起,将前一次操作中的好点作为本次操作的一个试验点,若每次操作后得到的存优区间长度与操作前区间的长度的比值为同一个常数
,可使存优区间长度逐步减小.为了方便找到最优点(或者接近最优点),从第二次操作起,将前一次操作中的好点作为本次操作的一个试验点,若每次操作后得到的存优区间长度与操作前区间的长度的比值为同一个常数 ,则称这样的操作是“优美的”,得到的每一个存优区间都称为优美存优区间,
,则称这样的操作是“优美的”,得到的每一个存优区间都称为优美存优区间, 称为优美存优区间常数.对区间
称为优美存优区间常数.对区间 进行
进行 次“优美的”操作,最后得到优美存优区间
次“优美的”操作,最后得到优美存优区间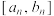 ,令
,令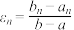 ,我们可任取区间
,我们可任取区间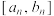 内的一个实数作为最优点
内的一个实数作为最优点 的近似值,称之为
的近似值,称之为 在区间
在区间 上精度为
上精度为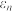 的“合规近似值”,记作
的“合规近似值”,记作 .已知函数
.已知函数 ,函数
,函数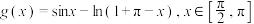 .
.(1)求证:函数
 是单峰函数;
是单峰函数;(2)已知
 为函数
为函数 的最优点,
的最优点, 为函数
为函数 的最优点.
的最优点.(i)求证:
 ;
;(ii)求证:
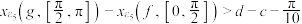 .
.注:
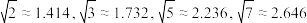 .
.
您最近一年使用:0次



