名校
解题方法
1 . 高斯是德国著名的数学家,近代数学奠基者之一,用其名字命名的“高斯函数”为:设 ,用
,用 表示不超过
表示不超过 的最大整数,则
的最大整数,则 称为高斯函数.例如:
称为高斯函数.例如: .已知函数
.已知函数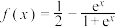 ,则函数
,则函数 的值域是
的值域是__________ .
 ,用
,用 表示不超过
表示不超过 的最大整数,则
的最大整数,则 称为高斯函数.例如:
称为高斯函数.例如: .已知函数
.已知函数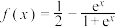 ,则函数
,则函数 的值域是
的值域是
您最近一年使用:0次
2024-01-02更新
|
1300次组卷
|
8卷引用:江苏省南通市海安高级中学2023-2024学年高一上学期12月月考数学试题
江苏省南通市海安高级中学2023-2024学年高一上学期12月月考数学试题福建省福州市九师教学联盟2023-2024学年高一上学期1月联考数学试题(已下线)专题04 指数函数与对数函数2-2024年高一数学寒假作业单元合订本安徽省合肥市合肥一中肥东分校2023-2024学年高一上学期期末数学试题(已下线)高一数学开学摸底考 02-北师大版2019必修第一册全册摸底考试卷单元测试A卷——第四章 指数函数与对数函数(已下线)【一题多变】分段高斯 取整数形(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练
名校
2 . 函数 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数,可以将其推广为:函数
为奇函数,可以将其推广为:函数 的图象关于点
的图象关于点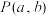 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数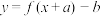 为y关于x的奇函数,给定函数
为y关于x的奇函数,给定函数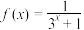 .
.
(1)求 的对称中心;
的对称中心;
(2)已知函数 ,若对任意的
,若对任意的 ,总存在
,总存在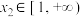 ,使得
,使得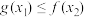 ,求实数
,求实数 的取值范围.
的取值范围.
 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数,可以将其推广为:函数
为奇函数,可以将其推广为:函数 的图象关于点
的图象关于点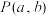 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数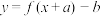 为y关于x的奇函数,给定函数
为y关于x的奇函数,给定函数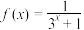 .
.(1)求
 的对称中心;
的对称中心;(2)已知函数
 ,若对任意的
,若对任意的 ,总存在
,总存在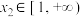 ,使得
,使得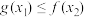 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-27更新
|
608次组卷
|
3卷引用:江苏省苏州中学校2023-2024学年高一上学期期中数学试卷
江苏省苏州中学校2023-2024学年高一上学期期中数学试卷(已下线)4.2.1指数函数的概念+4.2.2指数函数的图象和性质【第三练】湖北省鄂西南三校2023-2024学年高一上学期12月联考数学试题
名校
解题方法
3 . 已知指数函数 在其定义域内单调递增.
在其定义域内单调递增.
(1)求函数 的解析式;
的解析式;
(2)设函数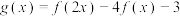 ,当
,当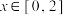 时.求函数
时.求函数 的值域.
的值域.
 在其定义域内单调递增.
在其定义域内单调递增.(1)求函数
 的解析式;
的解析式;(2)设函数
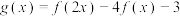 ,当
,当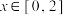 时.求函数
时.求函数 的值域.
的值域.
您最近一年使用:0次
2023-10-07更新
|
1987次组卷
|
19卷引用:江苏省平潮高级中学2023-2034学年高一上学期12月初数学双周练试题
江苏省平潮高级中学2023-2034学年高一上学期12月初数学双周练试题安徽省合肥市六校联盟2023-2024学年高一上学期11月期中考试数学试题安徽省合肥市重点中学2023-2024学年高一上学期期中联考数学试题甘肃省庆阳市环县第一中学2023-2024学年高一上学期第二次月考数学试题(已下线)第01讲 4.1指数+4.2指数函数—【练透核心考点】河南省洛阳市宜阳县第一高级中学2023-2024学年高一清北园研学班上学期期末考试数学试卷广东省湛江第一中学2023-2024学年高一上学期第二次大考数学试题甘肃省庆阳市第二中学2023-2024学年高一上学期期中考试数学试题山西省2024届高三上学期10月月考数学试题山西省金科大联考2024届高三上学期10月质量检测数学试题甘肃省酒泉市2023-2024学年高三上学期10月联考数学试题陕西省咸阳市永寿县中学2023-2024学年高三上学期第三次考试文科数学试题河南省郑州市宇华实验学校2023-2024学年高二上学期1月月考数学试题陕西省子长市中学2024届高三上学期第三次模拟考试理科数学试题(已下线)2.7指数函数(高三一轮)【讲】 (提升版)(已下线)指数与指数函数01-一轮复习考点专练甘肃省定西市临洮县第二中学2024届高三上学期期中考试数学试题安徽省六安市叶集皖西当代中学2024届高三上学期11月质量检测数学试卷贵州省铜仁市第八中学2024届高三上学期第四次月考数学试题
名校
解题方法
4 . 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设 ,用
,用 表示不超过
表示不超过 的最大整数,则
的最大整数,则 称为高斯函数,例如:
称为高斯函数,例如: ,
,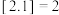 .已知函数
.已知函数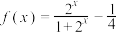 ,
,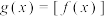 ,则下列叙述中错误的是( )
,则下列叙述中错误的是( )
 ,用
,用 表示不超过
表示不超过 的最大整数,则
的最大整数,则 称为高斯函数,例如:
称为高斯函数,例如: ,
,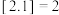 .已知函数
.已知函数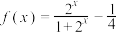 ,
,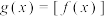 ,则下列叙述中错误的是( )
,则下列叙述中错误的是( )A. 在 在 上是增函数 上是增函数 | B. 是奇函数 是奇函数 |
C. 的值域是 的值域是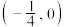 | D. 的值域是 的值域是 |
您最近一年使用:0次
2023-09-30更新
|
1495次组卷
|
11卷引用:第6章 幂函数、指数函数和对数函数综合能力测试-【帮课堂】(苏教版2019必修第一册)
(已下线)第6章 幂函数、指数函数和对数函数综合能力测试-【帮课堂】(苏教版2019必修第一册)(已下线)6.2 指数函数(2)-【帮课堂】(苏教版2019必修第一册)(已下线)模块二 专题4《幂函数、指数与指数函数》单元检测篇 A基础卷 (人教A)广东省广州九十七中2023-2024学年高一上学期期中数学试题广东省深圳市科学高中2023-2024学年高一上学期期中考试数学试题辽宁省六校协作体2023-2024学年高一上学期期中考试数学试题(已下线)4.2.1指数函数的概念+4.2.2指数函数的图象和性质【第三练】河南省南阳市第一中学校2023-2024学年高一上学期第二次月考数学试题河南省南阳市唐河县第一高级中学2023-2024学年高一上学期12月月考数学试题黑龙江省齐齐哈尔市地区普高联谊校2023-2024学年高三上学期9月月考数学试题山东省泰安市新泰第一中学老校区(新泰中学)2025届高三上学期第一次适应训练数学试题
5 . 已知函数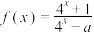 为奇函数.
为奇函数.
(1)求 的值
的值
(2)解不等式
(3)求 的值域.
的值域.
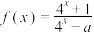 为奇函数.
为奇函数.(1)求
 的值
的值(2)解不等式

(3)求
 的值域.
的值域.
您最近一年使用:0次
6 . 已知函数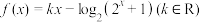 的图像关于
的图像关于 轴对称.
轴对称.
(1)求 的值;
的值;
(2)若函数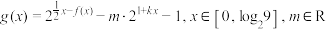 ,求
,求 的最大值
的最大值 .
.
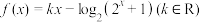 的图像关于
的图像关于 轴对称.
轴对称.(1)求
 的值;
的值;(2)若函数
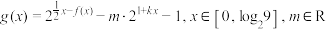 ,求
,求 的最大值
的最大值 .
.
您最近一年使用:0次
2023-09-07更新
|
496次组卷
|
3卷引用:第6章 幂函数、指数函数和对数函数章末题型归纳总结 (1)-【帮课堂】(苏教版2019必修第一册)
(已下线)第6章 幂函数、指数函数和对数函数章末题型归纳总结 (1)-【帮课堂】(苏教版2019必修第一册)河南省南阳市2022-2023学年高一上学期期末数学试题河南省洛阳市孟津区第一高级中学2023-2024学年高一上学期期末数学试题
22-23高一上·全国·期中
7 . 已知二次函数 ,关于实数
,关于实数 的不等式
的不等式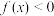 的解集为
的解集为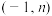
(1)当 时,解关于
时,解关于 的不等式:
的不等式: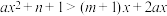
(2)是否存在实数 ,使得关于
,使得关于 的函数
的函数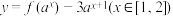 的最小值为
的最小值为 ?若存在,求实数
?若存在,求实数 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 ,关于实数
,关于实数 的不等式
的不等式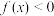 的解集为
的解集为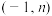
(1)当
 时,解关于
时,解关于 的不等式:
的不等式: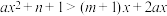
(2)是否存在实数
 ,使得关于
,使得关于 的函数
的函数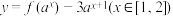 的最小值为
的最小值为 ?若存在,求实数
?若存在,求实数 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
8 . 已知函数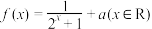 为奇函数,则( )
为奇函数,则( )
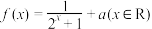 为奇函数,则( )
为奇函数,则( )A. | B. 为 为 上的增函数 上的增函数 |
C. 的解集为 的解集为 | D. 的值域为 的值域为 |
您最近一年使用:0次
2023-02-22更新
|
875次组卷
|
5卷引用:江苏省泰州市2022-2023学年高一上学期期末数学试题
江苏省泰州市2022-2023学年高一上学期期末数学试题江苏省2023-2024学年高一上学期期末全真模拟数学试题04(已下线)模块一 专题4 指数与指数函数(2)(人教A)广东省佛山市南海区艺术高级中学2023-2024学年高一上学期第二次月测(12月)数学试卷(已下线)专题05 指数函数与函数的应用1-期末复习重难培优与单元检测(人教A版2019)
解题方法
9 . 关于函数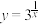 的性质,下列说法正确的是( )
的性质,下列说法正确的是( )
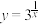 的性质,下列说法正确的是( )
的性质,下列说法正确的是( )A.定义域为 ; ; |
B.值域为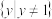 ; ; |
| C.在定义域上单调递减; |
| D.既不是奇函数也不是偶函数. |
您最近一年使用:0次
名校
10 . 已知函数 ,则( )
,则( )
 ,则( )
,则( )A.函数 的定义域为R 的定义域为R |
B.函数 的值域为 的值域为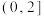 |
C.函数 在 在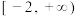 上单调递增 上单调递增 |
D.函数 在 在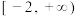 上单调递减 上单调递减 |
您最近一年使用:0次
2023-10-04更新
|
5057次组卷
|
26卷引用:6.2 指数函数(2)-【帮课堂】(苏教版2019必修第一册)
(已下线)6.2 指数函数(2)-【帮课堂】(苏教版2019必修第一册)广西浦北中学2021-2022学年高一上学期期中考试数学试题2023版 湘教版(2019) 必修第一册 突围者 第4章 专项拓展训练1 与指数函数有关的复合函数问题苏教版(2019) 必修第一册 突围者 第6章 专项拓展训练1 与指数函数有关的复合函数问题2023版 北师大版(2019) 必修第一册 突围者 第三章 专项拓展训练 与指数函数有关的复合函数问题(已下线)突破4.2 指数函数(重难点突破)-【新教材优创】突破满分数学之2022-2023学年高一数学重难点突破+课时训练 (人教A版2019必修第一册)重庆市合川中学2022-2023学年高一上学期期末数学试题河北省唐山英才国际学校2022-2023学年高一上学期11月月考数学试题浙江省台州市临海市学海中学2022-2023学年高一上学期12月质量评估(三)数学试题重庆市永川北山中学校2022-2023学年高一下学期入学考试数学试题广东省汕头经济特区林百欣中学2022-2023学年高一上学期期末数学试题第四章 指数函数与对数函数 核心02(已下线)重难点03函数(15种解题模型与方法)(1)(已下线)4.2 指数函数(重难点突破)-【冲刺满分】(已下线)专题4.8 指数函数与对数函数全章综合测试卷(基础篇)-举一反三系列(已下线)模块二 专题4《幂函数、指数与指数函数》单元检测篇 B提升卷(人教A)(已下线)高一数学上学期期中考试模拟卷-【巅峰课堂】热点题型归纳与培优练福建省厦门海沧实验中学2023-2024学年高一上学期11月阶段性测试数学试题山西省太原市杏花岭区山西省实验中学2023-2024学年高一上学期期中数学试题山东省泰安市新泰一中老校区(新泰中学)2023-2024学年高一上学期第二次月考数学试题(已下线)第四章 指数函数与对数函数-【优化数学】单元测试能力卷(人教A版2019)(已下线)第17讲 指数函数及性质八大题型总结(2)-【同步题型讲义】(人教A版2019必修第一册)专题08指数运算与指数函数江西省宜春市宜春一中、万载中学、宜丰中学2022-2023学年高二下学期期末考试数学试题江西省宜春市第一中学2022-2023学年高二下学期期末考试数学试题江西省贵溪市实验中学2024届高三9月(双向达标)月考数学试题



