1 . 已知函数 .
.
(1)若曲线 在点
在点 处的切线的斜率为-3,求a的值;
处的切线的斜率为-3,求a的值;
(2)求 的单调区间;
的单调区间;
(3)若 ,对任意
,对任意 ,
, ,
, ,不等式
,不等式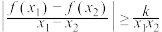 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
 .
.(1)若曲线
 在点
在点 处的切线的斜率为-3,求a的值;
处的切线的斜率为-3,求a的值;(2)求
 的单调区间;
的单调区间;(3)若
 ,对任意
,对任意 ,
, ,
, ,不等式
,不等式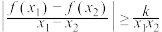 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
您最近一年使用:0次
名校
解题方法
2 . 已知函数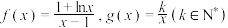 ,若对任意的
,若对任意的 ,存在实数
,存在实数 满足
满足 ,使得
,使得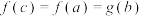 ,则k的最大值为( )
,则k的最大值为( )
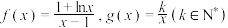 ,若对任意的
,若对任意的 ,存在实数
,存在实数 满足
满足 ,使得
,使得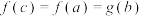 ,则k的最大值为( )
,则k的最大值为( )| A.3 | B.4 | C.5 | D.6 |
您最近一年使用:0次
3 . 已知函数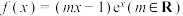 在
在 处取得极小值.
处取得极小值.
(1)求 的值;
的值;
(2)求函数 在点
在点 处的切线方程;
处的切线方程;
(3)若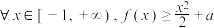 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
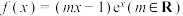 在
在 处取得极小值.
处取得极小值.(1)求
 的值;
的值;(2)求函数
 在点
在点 处的切线方程;
处的切线方程;(3)若
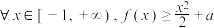 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
4 . 已知 为实数,函数
为实数,函数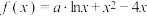 .
.
(1)是否存在实数 ,使得
,使得 在
在 处取极值?证明你的结论;
处取极值?证明你的结论;
(2)若函数 在
在 上存在单调递增区间,求实数
上存在单调递增区间,求实数 的取值范围;
的取值范围;
(3)设 ,若存在
,若存在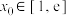 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 为实数,函数
为实数,函数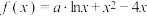 .
.(1)是否存在实数
 ,使得
,使得 在
在 处取极值?证明你的结论;
处取极值?证明你的结论;(2)若函数
 在
在 上存在单调递增区间,求实数
上存在单调递增区间,求实数 的取值范围;
的取值范围;(3)设
 ,若存在
,若存在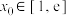 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
5 . 已知函数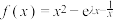 .
.
(1)当 时,求
时,求 的图象在点
的图象在点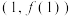 处的切线方程;
处的切线方程;
(2)若 时,
时,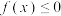 ,求
,求 的取值范围;
的取值范围;
(3)求证: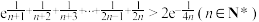 .
.
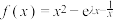 .
.(1)当
 时,求
时,求 的图象在点
的图象在点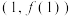 处的切线方程;
处的切线方程;(2)若
 时,
时,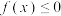 ,求
,求 的取值范围;
的取值范围;(3)求证:
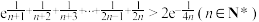 .
.
您最近一年使用:0次
2024-10-31更新
|
1676次组卷
|
3卷引用:天津市南开中学2025届高三上学期数学统练试卷3
6 . 已知函数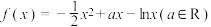 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求 的单调区间;
的单调区间;
(3)若函数 有两个极值点
有两个极值点 ,求证:
,求证: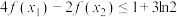 .
.
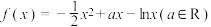 .
.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)求
 的单调区间;
的单调区间;(3)若函数
 有两个极值点
有两个极值点 ,求证:
,求证: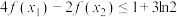 .
.
您最近一年使用:0次
名校
7 . 已知函数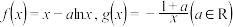 .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)设函数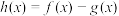 ,求函数
,求函数 的单调区间;
的单调区间;
(3)若在 上存在一点
上存在一点 ,使得
,使得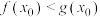 成立,求a的取值范围.
成立,求a的取值范围.
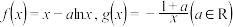 .
.(1)若
 ,求函数
,求函数 的极值;
的极值;(2)设函数
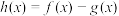 ,求函数
,求函数 的单调区间;
的单调区间;(3)若在
 上存在一点
上存在一点 ,使得
,使得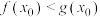 成立,求a的取值范围.
成立,求a的取值范围.
您最近一年使用:0次
2024-10-25更新
|
347次组卷
|
2卷引用:天津市实验中学2025届高三上学期第二次质量调查数学试卷
名校
8 . 已知函数 .
.
(1)求函数 的极值;
的极值;
(2)证明:对任意的 ,有
,有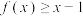 ;
;
(3)若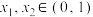 ,证明:
,证明: .
.
 .
.(1)求函数
 的极值;
的极值;(2)证明:对任意的
 ,有
,有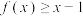 ;
;(3)若
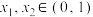 ,证明:
,证明: .
.
您最近一年使用:0次
2024-10-24更新
|
484次组卷
|
2卷引用:天津市第一中学2024-2025学年高三上学期十月份第一次月考数学试卷
名校
解题方法
9 . 已知函数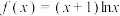 ,
,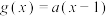 .
.
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)若 对任意的
对任意的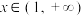 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若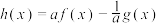 有三个零点
有三个零点 ,
, ,
, ,且
,且 ,求证:
,求证: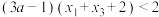 .
.
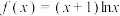 ,
,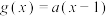 .
.(1)求曲线
 在
在 处的切线方程;
处的切线方程;(2)若
 对任意的
对任意的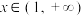 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
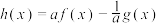 有三个零点
有三个零点 ,
, ,
, ,且
,且 ,求证:
,求证: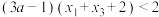 .
.
您最近一年使用:0次
2024-10-20更新
|
493次组卷
|
3卷引用:天津市第四十七中学2024-2025学年高三上学期10月月考数学试题
10 . (1)设 ,对任意实数x,记
,对任意实数x,记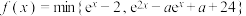 .若
.若 有三个零点,则实数a的取值范围.
有三个零点,则实数a的取值范围.
(2)已知函数 ,其中
,其中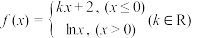 ,若方程
,若方程 有三个不同的实数根,则实数k的取值范围.
有三个不同的实数根,则实数k的取值范围.
(3)已知函数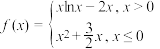 ,函数
,函数 有四个零点,则实数
有四个零点,则实数 的取值范围.
的取值范围.
(4)问题:用数形结合法解决函数零点问题是常用的方法,请总结此方法使用时需要注意什么问题?
 ,对任意实数x,记
,对任意实数x,记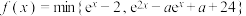 .若
.若 有三个零点,则实数a的取值范围.
有三个零点,则实数a的取值范围.(2)已知函数
 ,其中
,其中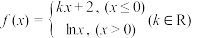 ,若方程
,若方程 有三个不同的实数根,则实数k的取值范围.
有三个不同的实数根,则实数k的取值范围.(3)已知函数
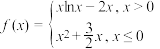 ,函数
,函数 有四个零点,则实数
有四个零点,则实数 的取值范围.
的取值范围.(4)问题:用数形结合法解决函数零点问题是常用的方法,请总结此方法使用时需要注意什么问题?
您最近一年使用:0次



