1 . 已知函数 (
( 为常数),函数
为常数),函数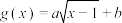 .
.
(1)若函数 有两个零点,求实数
有两个零点,求实数 的取值的范围;
的取值的范围;
(2)当 ,设函数
,设函数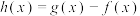 ,若
,若 在
在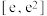 上有零点,求
上有零点,求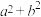 的最小值.
的最小值.
 (
( 为常数),函数
为常数),函数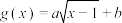 .
.(1)若函数
 有两个零点,求实数
有两个零点,求实数 的取值的范围;
的取值的范围;(2)当
 ,设函数
,设函数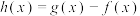 ,若
,若 在
在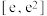 上有零点,求
上有零点,求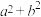 的最小值.
的最小值.
您最近一年使用:0次
解题方法
2 . 已知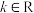 ,记
,记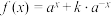 (
( 且
且 ).
).
(1)当 (
( 是自然对数的底)时,试讨论函数
是自然对数的底)时,试讨论函数 的单调性和最值;
的单调性和最值;
(2)试讨论函数 的奇偶性;
的奇偶性;
(3)拓展与探究:
① 当 在什么范围取值时,函数
在什么范围取值时,函数 的图象在
的图象在 轴上存在对称中心?请说明理由;
轴上存在对称中心?请说明理由;
②请提出函数 的一个新性质,并用数学符号语言表达出来.(不必证明)
的一个新性质,并用数学符号语言表达出来.(不必证明)
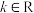 ,记
,记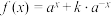 (
( 且
且 ).
).(1)当
 (
( 是自然对数的底)时,试讨论函数
是自然对数的底)时,试讨论函数 的单调性和最值;
的单调性和最值;(2)试讨论函数
 的奇偶性;
的奇偶性;(3)拓展与探究:
① 当
 在什么范围取值时,函数
在什么范围取值时,函数 的图象在
的图象在 轴上存在对称中心?请说明理由;
轴上存在对称中心?请说明理由;②请提出函数
 的一个新性质,并用数学符号语言表达出来.(不必证明)
的一个新性质,并用数学符号语言表达出来.(不必证明)
您最近一年使用:0次
2024-04-19更新
|
690次组卷
|
2卷引用:上海市静安区2024届高三下学期期中教学质量调研数学试卷
3 . 若函数 有3个不同的零点,分别记为
有3个不同的零点,分别记为 ,则下列说法正确的是( ).
,则下列说法正确的是( ).
 有3个不同的零点,分别记为
有3个不同的零点,分别记为 ,则下列说法正确的是( ).
,则下列说法正确的是( ).A. 是函数 是函数 的一个零点 的一个零点 |
B.a的取值范围是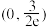 |
C. |
D.若 ,则a的范围是 ,则a的范围是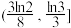 .(其中 .(其中 表示不超过实数x的最大整数,例如: 表示不超过实数x的最大整数,例如: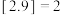 , , ) ) |
您最近一年使用:0次
名校
4 . 已知函数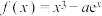 ,若函数
,若函数 有 3 个极值点
有 3 个极值点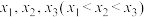 ,则实数
,则实数 的取 值范围是
的取 值范围是_______ ; 若 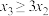 ,则实数
,则实数 的取值范围是
的取值范围是 _____
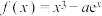 ,若函数
,若函数 有 3 个极值点
有 3 个极值点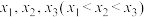 ,则实数
,则实数 的取 值范围是
的取 值范围是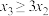 ,则实数
,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
名校
5 . 已知函数 .
.
(1)若函数 在定义域内单调递增,求实数
在定义域内单调递增,求实数 的范围;
的范围;
(2)若实数 ,求
,求 的单调递增区间;
的单调递增区间;
(3)若函数 有两个极值点
有两个极值点 且
且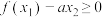 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)若函数
 在定义域内单调递增,求实数
在定义域内单调递增,求实数 的范围;
的范围;(2)若实数
 ,求
,求 的单调递增区间;
的单调递增区间;(3)若函数
 有两个极值点
有两个极值点 且
且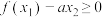 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-04-17更新
|
501次组卷
|
2卷引用:江苏省无锡市太湖高级中学2022-2023学年高二下学期期中数学试题
6 . 已知函数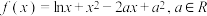 .
.
(1)若 ,求函数
,求函数 在
在 上的最小值;
上的最小值;
(2)若函数 在
在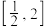 上存在单调递增区间,求实数
上存在单调递增区间,求实数 的取值范围;
的取值范围;
(3)根据 的不同取值,讨论函数
的不同取值,讨论函数 的极值点情况.
的极值点情况.
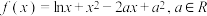 .
.(1)若
 ,求函数
,求函数 在
在 上的最小值;
上的最小值;(2)若函数
 在
在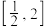 上存在单调递增区间,求实数
上存在单调递增区间,求实数 的取值范围;
的取值范围;(3)根据
 的不同取值,讨论函数
的不同取值,讨论函数 的极值点情况.
的极值点情况.
您最近一年使用:0次
2016-12-04更新
|
1420次组卷
|
2卷引用:2016届天津市和平区高三第四次模拟理科数学试卷
名校
7 . 已知 为实数,函数
为实数,函数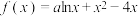 .
.
(1)若 是函数
是函数 的一个极值点,求实数
的一个极值点,求实数 的取值;
的取值;
(2)设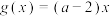 ,若
,若 ,使得
,使得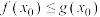 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 为实数,函数
为实数,函数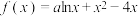 .
.(1)若
 是函数
是函数 的一个极值点,求实数
的一个极值点,求实数 的取值;
的取值;(2)设
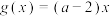 ,若
,若 ,使得
,使得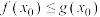 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2017-09-23更新
|
1448次组卷
|
8卷引用:广西桂林市柳州市2018年届高三综合模拟金卷(1)理科数学试题
广西桂林市柳州市2018年届高三综合模拟金卷(1)理科数学试题广西桂林市柳州市2018年届高三综合模拟金卷(1)文科数学试题山东省栖霞市第一中学2018届高三4月模拟考试数学(理)试题黑龙江省牡丹江市第一高级中学2018-2019学年高二下学期期末数学(文)试题四川省宜宾市叙州区第一中学校2019-2020学年高二下学期第四学月考试数学(文)试题陕西省榆林市定边县第四中学2023届高三上学期第二次月考理科数学试题安徽省合肥市庐江县五校2022-2023学年高三上学期期末联考数学试题(已下线)第七章 导数与不等式能成立(有解)问题 专题一 单变量不等式能成立(有解)之参变分离法 微点1 单变量不等式能成立(有解)之参变分离法
名校
解题方法
8 . 已知函数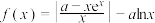 .
.
(1)当 时,求不等式
时,求不等式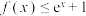 的解集;
的解集;
(2)若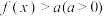 ,求实数
,求实数 的取值范围.
的取值范围.
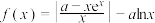 .
.(1)当
 时,求不等式
时,求不等式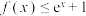 的解集;
的解集;(2)若
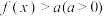 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
9 . 已知函数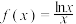 ,设
,设 ,若
,若 只有一个零点,则实数a的取值范围是
只有一个零点,则实数a的取值范围是______ ;若不等式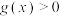 的解集中有且只有三个整数,则实数a的取值范围是
的解集中有且只有三个整数,则实数a的取值范围是______ .
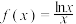 ,设
,设 ,若
,若 只有一个零点,则实数a的取值范围是
只有一个零点,则实数a的取值范围是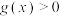 的解集中有且只有三个整数,则实数a的取值范围是
的解集中有且只有三个整数,则实数a的取值范围是
您最近一年使用:0次
2024-06-14更新
|
119次组卷
|
2卷引用:山东省潍坊市2023-2024学年高二下学期期中考试数学试题
名校
解题方法
10 . 已知函数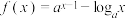 ,
, .
.
(1)若 ,求证:
,求证: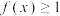 ;
;
(2)若关于 的不等式
的不等式 的解集为集合
的解集为集合 ,且
,且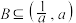 ,求实数
,求实数 的取值范围.
的取值范围.
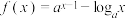 ,
, .
.(1)若
 ,求证:
,求证: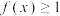 ;
;(2)若关于
 的不等式
的不等式 的解集为集合
的解集为集合 ,且
,且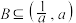 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-05-05更新
|
1162次组卷
|
3卷引用:江苏省南京市2023届高三二模数学试题



