解题方法
1 . 已知向量 ,
, 满足
满足 ,
, ,
, .
.
(1)求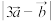 ;
;
(2)若向量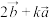 与
与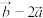 相互垂直,求实数
相互垂直,求实数 的值.
的值.
 ,
, 满足
满足 ,
, ,
, .
.(1)求
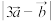 ;
;(2)若向量
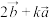 与
与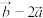 相互垂直,求实数
相互垂直,求实数 的值.
的值.
您最近一年使用:0次
2024-07-24更新
|
318次组卷
|
2卷引用:陕西省榆林市2023-2024学年高一下学期期末数学试卷
2 . 已知 中,内角
中,内角 的对边分别为
的对边分别为 、
、 、
、 ,点
,点 为边
为边 上一点,满足
上一点,满足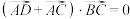 .
.
(1)求证: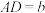 ;
;
(2)若 为内角A的角平分线,满足
为内角A的角平分线,满足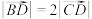 ,求
,求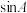 .
.
 中,内角
中,内角 的对边分别为
的对边分别为 、
、 、
、 ,点
,点 为边
为边 上一点,满足
上一点,满足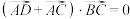 .
.(1)求证:
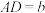 ;
;(2)若
 为内角A的角平分线,满足
为内角A的角平分线,满足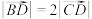 ,求
,求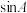 .
.
您最近一年使用:0次
解题方法
3 . 在锐角三角形 中,内角
中,内角 所对应的边分别为
所对应的边分别为 ,
, ,
, ,点
,点 ,
, 分别为边
分别为边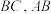 的中点,满足
的中点,满足 .
.
(1)求边 ,
, ,
, 之间的关系;
之间的关系;
(2)求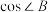 的值域.
的值域.
 中,内角
中,内角 所对应的边分别为
所对应的边分别为 ,
, ,
, ,点
,点 ,
, 分别为边
分别为边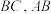 的中点,满足
的中点,满足 .
.(1)求边
 ,
, ,
, 之间的关系;
之间的关系;(2)求
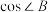 的值域.
的值域.
您最近一年使用:0次
解题方法
4 . 如图,在 中,
中,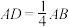 ,点
,点 分别是
分别是 的中点.设
的中点.设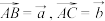 .
.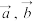 表示
表示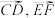 ;
;
(2)如果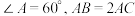 ,请判断
,请判断 的位置关系?用向量方法证明你的结论.
的位置关系?用向量方法证明你的结论.
 中,
中, ,点
,点 分别是
分别是 的中点.设
的中点.设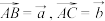 .
.
 表示
表示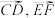 ;
;(2)如果
 ,请判断
,请判断 的位置关系?用向量方法证明你的结论.
的位置关系?用向量方法证明你的结论.
您最近一年使用:0次
名校
解题方法
5 . 已知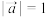 ,
, ,
, 与
与 的夹角为
的夹角为 .
.
(1)求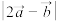 ;
;
(2)若向量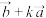 与
与 相互垂直,求实数k的值.
相互垂直,求实数k的值.
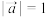 ,
, ,
, 与
与 的夹角为
的夹角为 .
.(1)求
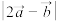 ;
;(2)若向量
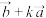 与
与 相互垂直,求实数k的值.
相互垂直,求实数k的值.
您最近一年使用:0次
2024-04-05更新
|
771次组卷
|
9卷引用:陕西省咸阳市三原县北城中学2023-2024学年高一下学期第一次月考数学试题
陕西省咸阳市三原县北城中学2023-2024学年高一下学期第一次月考数学试题河南省新乡市封丘县第一中学2023-2024学年高一下学期期中数学试题广东省茂名市信宜市信宜中学2023-2024学年高一下学期4月期中考试数学试题青海省西宁市第十四中学2023-2024学年高一下学期期中考试数学试卷(已下线)专题03 向量的数量积-期末考点大串讲(人教B版2019必修第三册)安徽省亳州市第二完全中学2023-2024学年高一下学期第二次月考(5月)数学试题江苏省扬州市树人学校2023-2024学年高一下学期期中调研数学试卷四川省成都市简阳实验学校2023-2024学年高一下学期5月月考数学试题新疆阿克苏市实验中学2023-2024学年高一下学期第二次月考数学试题
23-24高一·全国·假期作业
名校
解题方法
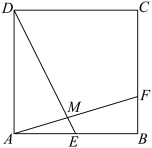
6 . 如图,正方形 的边长为
的边长为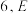 是
是 的中点,
的中点, 是
是 边上靠近点
边上靠近点 的三等分点,
的三等分点, 与
与 交于点
交于点 .
. 的余弦值.
的余弦值.
(2)若点 自
自 点逆时针沿正方形的边运动到
点逆时针沿正方形的边运动到 点,在这个过程中,是否存在这样的点
点,在这个过程中,是否存在这样的点 ,使得
,使得 ?若存在,求出
?若存在,求出 的长度,若不存在,请说明理由.
的长度,若不存在,请说明理由.
 的边长为
的边长为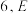 是
是 的中点,
的中点, 是
是 边上靠近点
边上靠近点 的三等分点,
的三等分点, 与
与 交于点
交于点 .
.
 的余弦值.
的余弦值.(2)若点
 自
自 点逆时针沿正方形的边运动到
点逆时针沿正方形的边运动到 点,在这个过程中,是否存在这样的点
点,在这个过程中,是否存在这样的点 ,使得
,使得 ?若存在,求出
?若存在,求出 的长度,若不存在,请说明理由.
的长度,若不存在,请说明理由.
您最近一年使用:0次
2024-02-17更新
|
761次组卷
|
8卷引用:陕西省西安市雁塔区第二中学2023-2024学年高一下学期第一次阶段性测评数学试题
陕西省西安市雁塔区第二中学2023-2024学年高一下学期第一次阶段性测评数学试题(已下线)第9章:平面向量章末检测卷-【寒假自学课】(苏教版2019)(已下线)6.3.5平面向量数量积的坐标表示【第三练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)6.3.5平面向量数量积的坐标表示(已下线)8.1.3向量数量积的坐标运算-同步精品课堂(人教B版2019必修第三册)(已下线)2.5 从力的做功到向量的数量积-同步精品课堂(北师大版2019必修第二册)广东省广州市西关外国语学校2023-2024学年高一下学期3月月考数学试题(已下线)高一下学期期中复习解答题压轴题十八大题型专练(1)-举一反三系列(人教A版2019必修第二册)
名校
解题方法
7 . 已知向量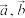 ,若
,若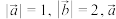 与
与 的夹角为
的夹角为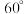 .
.
(1)求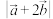 ;
;
(2)当 为何值时,向量
为何值时,向量 与向量
与向量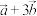 互相垂直?
互相垂直?
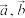 ,若
,若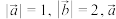 与
与 的夹角为
的夹角为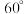 .
.(1)求
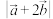 ;
;(2)当
 为何值时,向量
为何值时,向量 与向量
与向量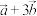 互相垂直?
互相垂直?
您最近一年使用:0次
2024-06-15更新
|
491次组卷
|
16卷引用:陕西省宝鸡南山高级中学2023-2024学年高一下学期阶段一数学试题
陕西省宝鸡南山高级中学2023-2024学年高一下学期阶段一数学试题云南省曲靖市民族中学2022-2023学年高一下学期期中考试数学试题湖南省邵阳市第二中学2022-2023学年高一下学期期末数学试题(已下线)第八章 平面向量(单元重点综合测试)-单元速记·巧练(沪教版2020必修第二册)黑龙江省齐齐哈尔市克东县第一中学等学校2023-2024学年高一下学期4月月考数学试题河南省河南名校联考2023-2024学年高一下学期4月月考数学试题吉林省四平市第一高级中学2023-2024学年高二上学期期初验收考试数学试题云南省曲靖市沾益区第一中学2023-2024学年高一下学期第一次月考数学试题青海省海东市第一中学2023-2024学年高一下学期第一次月考数学试题云南省曲靖市马龙区第一中学2023-2024学年高一下学期3月月考数学试题(已下线)专题03 向量的数量积-【暑假自学课】(人教B版2019必修第三册)云南省昆明市嵩明县昆一中嵩明学校(嵩明县第一中学)2023-2024学年高一下学期3月月考数学试题青海省海东市民和回族土族自治县城西高级中学2023-2024学年高一下学期3月月考数学试题甘肃省安阳市环县第四中学2023-2024学年高一下学期期中考试数学试题云南省曲靖市会泽县东陆高级中学校2023-2024学年高一下学期4月月考数学试题贵州省铜仁市德江县第二中学2023-2024学年高一下学期第一次月考数学试题
名校
解题方法
8 . 已知平面向量 ,
, ,
,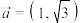 ,
, ,且
,且 与
与 的夹角为
的夹角为
(1)求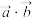
(2)若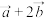 与
与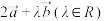 垂直,求
垂直,求 的值
的值
 ,
, ,
,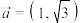 ,
, ,且
,且 与
与 的夹角为
的夹角为
(1)求
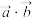
(2)若
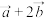 与
与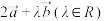 垂直,求
垂直,求 的值
的值
您最近一年使用:0次
2023-08-11更新
|
330次组卷
|
4卷引用:陕西省渭南市富平县2023-2024学年高一下学期期末质量数学试卷
陕西省渭南市富平县2023-2024学年高一下学期期末质量数学试卷辽宁省丹东市敬业实验高级中学2022-2023学年高一下学期期中数学试题新疆生产建设兵团第三师图木舒克市第一中学2022-2023学年高一下学期6月月考数学试题(已下线)第6.2.4讲 向量的数量积运算(第2课时)-精讲精练宝典
名校
解题方法
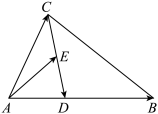
9 . 如图,在 中,
中,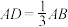 ,点
,点 是
是 的中点,设
的中点,设 ,
, 表示
表示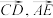 ;
;
(2)如果 ,
,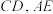 有什么位置关系?用向量方法证明你的结论.
有什么位置关系?用向量方法证明你的结论.
 中,
中,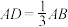 ,点
,点 是
是 的中点,设
的中点,设 ,
,
 表示
表示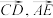 ;
;(2)如果
 ,
,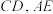 有什么位置关系?用向量方法证明你的结论.
有什么位置关系?用向量方法证明你的结论.
您最近一年使用:0次
2023-07-16更新
|
466次组卷
|
7卷引用:陕西省汉中市2024-2025学年高二上学期开学收心检测数学试卷
陕西省汉中市2024-2025学年高二上学期开学收心检测数学试卷福建省漳州市2022-2023学年高一下学期期末教学质量检测数学试题四川省成都市成飞中学2023-2024学年高二上学期入学考试数学试题(已下线)6.3.1 平面向量基本定理【第二练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)第06讲 6.3.1平面向量基本定理-【帮课堂】(人教A版2019必修第二册)(已下线)6.3.1 平面向量基本定理——课后作业(提升版)福建省福州第三中学2023-2024学年高一下学期4月期中数学试题
名校
解题方法
10 . 已知向量满足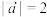 ,
, ,且
,且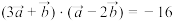 .
.
(1)若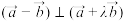 ,求实数
,求实数 的值;
的值;
(2)求 与
与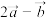 的夹角的余弦值.
的夹角的余弦值.
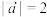 ,
, ,且
,且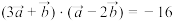 .
.(1)若
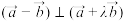 ,求实数
,求实数 的值;
的值;(2)求
 与
与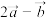 的夹角的余弦值.
的夹角的余弦值.
您最近一年使用:0次
2023-03-27更新
|
1078次组卷
|
14卷引用:陕西省渭南市富平县蓝光中学2023-2024学年高一下学期5月期中考试数学试题
陕西省渭南市富平县蓝光中学2023-2024学年高一下学期5月期中考试数学试题河南省高中名校联考2022-2023学年高一下期3月调研考试数学试题河南省洛阳市强基联盟2022-2023学年高一下学期3月月考数学试题河南省新高中创新联盟TOP二十名校2022-2023学年高一下学期3月调研考试数学试题江西省赣州市六校联盟2022-2023学年高一5月联考数学试题江西省赣州市兴国中学、兴国平川中学2022-2023学年高一下学期5月联合测评数学试题辽宁省凌源市普通高中2022-2023学年高一下学期6月联考数学试题江苏省无锡市四校2022-2023学年高一下学期期中联考数学试题四川省宜宾市第四中学校2022-2023学年高一下学期4月月考数学试题河南省洛阳市第四高级中学2022-2023学年高一下学期5月月考数学试题四川省仁寿第一中学校(北校区)2023-2024学年高一下学期3月质量检测数学试题江苏高一专题03平面向量(第二部分)四川省眉山市仁寿第一中学校南校区2023-2024学年高一下学期4月期中考试数学试题江西省南昌市第十中学2023-2024学年高一下学期第二次月考数学试题



