1 . 古希腊著名的约瑟夫环问题讲的是:共有127个士兵,围成一个环,从一号位的士兵开始,每个存活下来的人依次杀死相邻的下一位士兵,若一名叫做约瑟夫的士兵想要存活到最后,那么他最开始应当站在几号位上?( )
| A.1 | B.63 | C.127 | D.31 |
您最近一年使用:0次
名校
2 . 设数列 的各项均为非零的整数,其前
的各项均为非零的整数,其前 项和为
项和为 .若
.若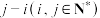 为正偶数,均有
为正偶数,均有 ,且
,且 ,则
,则 的最小值为( )
的最小值为( )
 的各项均为非零的整数,其前
的各项均为非零的整数,其前 项和为
项和为 .若
.若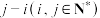 为正偶数,均有
为正偶数,均有 ,且
,且 ,则
,则 的最小值为( )
的最小值为( )| A.0 | B.22 | C.26 | D.31 |
您最近一年使用:0次
2024-05-10更新
|
943次组卷
|
4卷引用:北京市海淀区2023-2024学年高三下学期期末练习(二模)数学试题
北京市海淀区2023-2024学年高三下学期期末练习(二模)数学试题湖南省怀化市沅陵县第一中学2023-2024学年高二下学期期末考试数学试题广东省部分学校2025届高三上学期新起点模拟考试数学试题(已下线)周测13数列通项公式、求和(高三大一轮-北京专版)
3 . 17到19世纪间,数学家们研究了用连分式求解代数方程的根,并得到连分式的一个重要功能:用其逼近实数求近似值.例如,把方程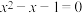 改写成
改写成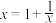 ①,将
①,将 再代入等式右边得到
再代入等式右边得到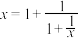 ,继续利用①式将
,继续利用①式将 再代入等式右边得到
再代入等式右边得到 ……反复进行,取
……反复进行,取 时,由此得到数列
时,由此得到数列 ,
, ,
, ,
,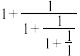 ,
, ,记作
,记作 ,则当
,则当 足够大时,
足够大时, 逼近实数
逼近实数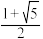 .数列
.数列 的前2024项中,满足
的前2024项中,满足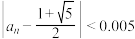 的
的 的个数为(参考数据:
的个数为(参考数据: )
)
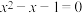 改写成
改写成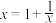 ①,将
①,将 再代入等式右边得到
再代入等式右边得到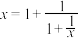 ,继续利用①式将
,继续利用①式将 再代入等式右边得到
再代入等式右边得到 ……反复进行,取
……反复进行,取 时,由此得到数列
时,由此得到数列 ,
, ,
, ,
, ,
, ,记作
,记作 ,则当
,则当 足够大时,
足够大时, 逼近实数
逼近实数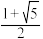 .数列
.数列 的前2024项中,满足
的前2024项中,满足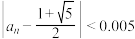 的
的 的个数为(参考数据:
的个数为(参考数据: )
)| A.1007 | B.1009 | C.2014 | D.2018 |
您最近一年使用:0次
2023-12-02更新
|
1343次组卷
|
5卷引用:广东省2024届高三上学期11月统一调研测试数学试题
广东省2024届高三上学期11月统一调研测试数学试题重庆市北碚区缙云教育联盟2024届高考零诊数学试题江苏省南京市南京师大附中2024届高三寒假模拟测试数学试题(已下线)专题04 数列及求和(分层练)(四大题型+14道精选真题)江苏省南京市第一中学2025届高三暑期阶段性测试数学试卷
名校
解题方法
4 . 已知数列 满足
满足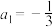 ,且
,且 ,若使不等式
,若使不等式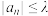 成立的
成立的 有且只有三项,则
有且只有三项,则 的取值范围为( )
的取值范围为( )
 满足
满足 ,且
,且 ,若使不等式
,若使不等式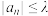 成立的
成立的 有且只有三项,则
有且只有三项,则 的取值范围为( )
的取值范围为( )A. | B.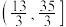 |
C.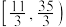 | D.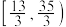 |
您最近一年使用:0次
2023-11-27更新
|
861次组卷
|
3卷引用:四川省2024届高三上学期第三次联考(月考)理科数学试题
5 . 已知 是数列
是数列 的前
的前 项和,且
项和,且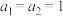 ,
,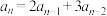 (
( ),则下列结论正确的是( )
),则下列结论正确的是( )
 是数列
是数列 的前
的前 项和,且
项和,且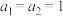 ,
,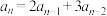 (
( ),则下列结论正确的是( )
),则下列结论正确的是( )A.数列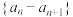 为等比数列 为等比数列 | B.数列 为等比数列 为等比数列 |
C.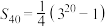 | D.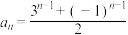 |
您最近一年使用:0次
2023-01-12更新
|
4727次组卷
|
9卷引用:湖北省部分重点中学2023届高三上学期1月第二次联考数学试题
湖北省部分重点中学2023届高三上学期1月第二次联考数学试题(已下线)专题5 数列 第2讲 数列通项与求和山东省安丘市青云学府2023届高三下学期一模数学试题(已下线)专题17 数列综合应用-3(已下线)专题10 数列通项公式的求法 微点4 奇偶分析法江苏省仪征市精诚高级中学2022-2023学年高三二模数学试题湖北省恩施州高中教育联盟2023届高三上学期期末数学试题(已下线)等差数列与等比数列北京市第九中学2023-2024学年高二下学期4月月考数学试卷
名校
解题方法
6 . 已知数列 中,
中, ,且
,且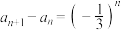 ,若存在正整数
,若存在正整数 ,使得
,使得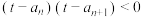 成立,则实数
成立,则实数 的取值范围为( )
的取值范围为( )
 中,
中, ,且
,且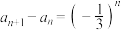 ,若存在正整数
,若存在正整数 ,使得
,使得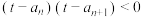 成立,则实数
成立,则实数 的取值范围为( )
的取值范围为( )A. | B. |
C. | D.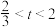 |
您最近一年使用:0次
2023-02-09更新
|
1284次组卷
|
2卷引用:河北省沧州市2023届高三上学期12月教学质量监测调研数学试题
名校
解题方法
7 . 数列 满足
满足 ,
,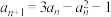 ,则下列说法错误的是( )
,则下列说法错误的是( )
 满足
满足 ,
,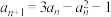 ,则下列说法错误的是( )
,则下列说法错误的是( )A.若 且 且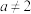 ,数列 ,数列 单调递减 单调递减 |
B.若存在无数个自然数 ,使得 ,使得 ,则 ,则 |
C.当 或 或 时, 时, 的最小值不存在 的最小值不存在 |
D.当 时, 时, |
您最近一年使用:0次
2022-09-23更新
|
2126次组卷
|
6卷引用:THUSSAT中学生标准学术能力2022-2023年度高三诊断性测试9月测试数学(理科)试题
THUSSAT中学生标准学术能力2022-2023年度高三诊断性测试9月测试数学(理科)试题(已下线)上海市华东师范大学第二附属中学2022-2023学年高二上学期9月阶段数学试题(已下线)专题17 数列(练习)-2湖北省襄阳市第五中学2022-2023学年高三上学期12月月考数学试题(已下线)第4章 数列(基础、典型、易错、压轴)(已下线)模块三 专题3 小题满分挑战练(3) 期末终极研习室(高二人教A版)
8 . 设数列 的前n项和为
的前n项和为 ,已知
,已知 ,
,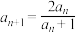 ,
,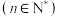 ,若
,若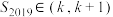 ,则正整数k的值为( )
,则正整数k的值为( )
 的前n项和为
的前n项和为 ,已知
,已知 ,
,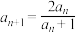 ,
,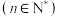 ,若
,若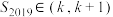 ,则正整数k的值为( )
,则正整数k的值为( )| A.2016 | B.2017 | C.2018 | D.2019 |
您最近一年使用:0次
9 . 已知数列 满足
满足 ,
,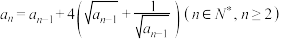 ,
, 为数列
为数列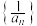 的前n项和,则( )
的前n项和,则( )
 满足
满足 ,
,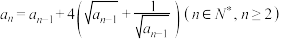 ,
, 为数列
为数列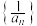 的前n项和,则( )
的前n项和,则( )A.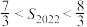 | B.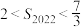 | C. | D.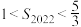 |
您最近一年使用:0次
2022-04-23更新
|
1893次组卷
|
6卷引用:浙江省嘉兴市2022届高三下学期4月教学测试(二模)数学试题
浙江省嘉兴市2022届高三下学期4月教学测试(二模)数学试题浙江省2022届高三下学期高考冲刺卷(二)数学试题(已下线)考点13 数列概念及通项公式(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)浙江省嘉兴市嘉善中学2022届高三下学期5月适应性考试数学试题(已下线)专题6-1 数列函数性质与不等式放缩(讲+练)-1(已下线)第23题 递推关系与数列求和(高三备考)
名校
10 . 已知各项均为正数的数列 满足
满足 ,
, ,则数列
,则数列 ( )
( )
 满足
满足 ,
, ,则数列
,则数列 ( )
( )| A.无最小项,无最大项 | B.无最小项,有最大项 |
| C.有最小项,无最大项 | D.有最小项,有最大项 |
您最近一年使用:0次
2022-04-08更新
|
1598次组卷
|
7卷引用:浙江省绍兴市2022届高三下学期4月高考科目适应性考试数学试题
浙江省绍兴市2022届高三下学期4月高考科目适应性考试数学试题(已下线)临考押题卷02-2022年高考数学临考押题卷(浙江卷)安徽省六安市舒城中学2022届高三下学期仿真模拟(三)理科数学试题浙江省2022届高三下学期6月高考数学仿真模拟卷01(已下线)专题2 数列的最大项与最小项 微点3 判断数列的最大(小)项之导数法(已下线)专题6-1 数列函数性质与不等式放缩(讲+练)-1(已下线)【练】专题3 数列范围(最值)问题



