1 . 已知数列 满足
满足 ,
, ,设
,设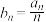 .
.
(1)求 ;
;
(2)判断数列 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(3)求 的通项公式.
的通项公式.
 满足
满足 ,
, ,设
,设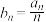 .
.(1)求
 ;
;(2)判断数列
 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;(3)求
 的通项公式.
的通项公式.
您最近一年使用:0次
2018-06-09更新
|
41280次组卷
|
81卷引用:重庆市第二十九中2020-2021学年高二上学期期中(半期)数学试题
重庆市第二十九中2020-2021学年高二上学期期中(半期)数学试题(已下线)2019年5月16日 《每日一题》(文科)—— 等差数列与等比数列专题11 数列(2)(已下线)步步高高二数学寒假作业:作业5等比数列(已下线)【新东方】杭州高二数学试卷233(已下线)【新东方】杭州高二数学试卷242湖北省宜昌市葛洲坝中学2018-2019学年高二上学期期中数学(文)试题(已下线)2.4等比数列(1) -2020-2021学年高二 数学课时同步练(人教A版必修5)浙江省杭州市高级中学2019-2020学年高二上学期期中数学试题云南省昆明市官渡区第一中学2019-2020学年高二下学期期中考试数学(文)试题陕西省渭南市临渭区尚德中学2020-2021学年高二上学期第一次月考数学试题人教A版(2019) 选择性必修第二册 过关斩将 第四章 数列 4.1-4.4综合拔高练(已下线)第四章 数列单元测试(巅峰版)-【新教材优创】突破满分数学之2020-2021学年高二数学重难点突破(人教A版2019选择性必修第二册)(已下线)第四章 数列单元测试(基础版)-【新教材优创】突破满分数学之2020-2021学年高二数学重难点突破(人教A版2019选择性必修第二册)(已下线)突破4.1 数列的概念课时训练-【新教材优创】突破满分数学之2020-2021学年高二数学课时训练(人教A版2019选择性必修第二册) 四川省仁寿第一中学校南校区2020-2021学年高二5月第二次质量检测数学(理)试题四川省仁寿第一中学校南校区2020-2021学年高二5月第二次质量检测数学(文)试题苏教版(2019) 选修第一册 突围者 第4章 章末培优专练(已下线)专题五 等比数列-2020-2021学年高中数学专题题型精讲精练(2019人教B版选择性必修第三册)(已下线)4.3.1 等比数列(1)-2020-2021学年高二数学课时同步练(人教A版选择性必修第二册)甘肃省张掖市第二中学2021-2022学年高二上学期10月月考数学 理科(B)试题(已下线)专题1.1 数列 章末检测1(易)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(人教A版2019选择性必修第二册)福建省厦门海沧实验中学2021-2022学年高二下学期6月阶段性检测数学试题2023版 湘教版(2019) 选修第一册 过关斩将 第1章 1.3.1等比数列及其通项公式+1.3.2等比数列与指数函数4.3.1 等比数列的概念练习福建省福州市六校2023-2024学年高二上学期期末联考数学试题(已下线)重难点02:求数列前n项和常用10种解题策略-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)5.3.1 等比数列(5知识点+6题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)【典例题】4.2.1 等比数列及其通项公式 课堂例题-沪教版(2020)选择性必修第一册第4章 数列【温故练】第1章 数列 章末复习课(二)单元测试-湘教版(2019)选择性必修第一册2018年全国普通高等学校招生统一考试文科数学(新课标I卷)(已下线)2018年高考题及模拟题汇编 【文科】4.数列与不等式【全国市级联考】湖北省黄冈市2018年春季高一期末考试文科数学试题【全国市级联考】湖北省黄冈市2017-2018学年高一下学期期末考试数学(文)试题(已下线)第01讲 数列的概念与简单表示法(练)-《2020年高考一轮复习讲练测》(浙江版)(已下线)第03讲 等比数列及其前n项和(讲)-《2020年高考一轮复习讲练测》(浙江版)专题6.1 数列的概念与简单表示法(练)【文】—《2020年高考一轮复习讲练测》(已下线)专题6.1 数列的概念与简单表示法(练)【理】-《2020年高考一轮复习讲练测》(已下线)专题6.3 等比数列及其前n项和(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题6.1 数列的概念与简单表示法(练)-江苏版《2020年高考一轮复习讲练测》江西省赣州市南康区2019-2020学年高一下学期线上教学检测数学试题(二)(已下线)专题05 等差数列和等比数列的证明问题(第二篇)-备战2020年高考数学大题精做之解答题题型全覆盖浙江省杭州市萧山中学2017-2018学年学业水平测试数学试题(已下线)题型09 求数列通项-2020届秒杀高考数学题型之数列(已下线)专题12 数列——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题6.3 等比数列及其前n项和-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破(已下线)专题14 数列综合-五年(2016-2020)高考数学(文)真题分项(已下线)专题18 等差数列与等比数列-十年(2011-2020)高考真题数学分项(已下线)考点20 数列的概念与简单表示法-备战2021年高考数学(文)一轮复习考点一遍过(已下线)考点22 等比数列及其前n项和-备战2021年高考数学(文)一轮复习考点一遍过(已下线)专题6.3 等比数列及其前n项和(精讲)-2021届高考数学(文)一轮复习讲练测(已下线)专题7.3 等比数列及其前n项和(精讲)-2021年新高考数学一轮复习学与练(已下线)专题6.3 等比数列及其前n项和(精讲)-2021年高考数学(文)一轮复习学与练(已下线)专题6.3 等比数列及其前n项和(精讲)-2021年高考数学(理)一轮复习学与练(已下线)专题6.3 等比数列及其前n项和(精讲)-2021届高考数学(理)一轮复习讲练测(已下线)专题4.2 数列-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)专题7.3 等比数列及其前n项和(讲)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)专题29等比数列通项与前n项和-2022年(新高考)数学高频考点+重点题型(已下线)第28讲 等比数列及其前n项和(讲)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)考点22 等比数列及其前n项和-备战2022年高考数学(文)一轮复习考点帮(已下线)考点23 已知递推公式求同通项公式求数列的通项公式-备战2022年高考数学(文)一轮复习考点帮(已下线)考点20 数列的概念与简单表示法-备战2022年高考数学(文)一轮复习考点帮(已下线)专题07 数列及其应用-十年(2012-2021)高考数学真题分项汇编(全国通用)人教B版(2019) 选修第三册 突围者 第五章 高考挑战(已下线)考点41 等比数列-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】(已下线)专题18等比数列-2022年高三毕业班数学常考点归纳与变式演练(文理通用)(已下线)专题08 数列-五年(2017-2021)高考数学真题分项汇编(文科+理科)青海省西宁市2021-2022学年高三上学期期末联考数学(理)试题青海省西宁市2021-2022学年高三上学期期末联考数学(文)试题(已下线)专题12 盘点等差(比)数列的判断与证明——备战2022年高考数学二轮复习常考点专题突破(已下线)专题22 等差等比数列性质的巧用-学会解题之高三数学万能解题模板【2022版】(已下线)类型二 等比数列-【题型突破】备战2022年高考数学二轮基础题型+重难题型突破(新高考专用)(已下线)专题05 数列解答题(已下线)第41讲 等比数列宁夏青铜峡市宁朔中学2023届高三上学期开学考试数学(文)试题(已下线)专题6 等比数列的判断(证明)方法 微点1 定义法、等比中项法(已下线)考点4 等比数列的定义与判断 2024届高考数学考点总动员(已下线)专题30 等比数列通项与前n项和(已下线)专题21 数列解答题(文科)-1专题29数列解答题(已下线)第04讲 数列的通项公式(十八大题型)(练习)-2
名校
2 . 学校食堂为了减少排队时间,从开学第 天起,每餐只推出即点即取的米饭套餐和面食套餐.某同学每天中午都会在食堂提供的两种套餐中选择一种套餐,若他前
天起,每餐只推出即点即取的米饭套餐和面食套餐.某同学每天中午都会在食堂提供的两种套餐中选择一种套餐,若他前 天选择了米饭套餐,则第
天选择了米饭套餐,则第 天选择米饭套餐的概率为
天选择米饭套餐的概率为 ;若他前
;若他前 天选择了面食套餐,则第
天选择了面食套餐,则第 天选择米饭套餐的概率为
天选择米饭套餐的概率为 .已知他开学第
.已知他开学第 天中午选择米饭套餐的概率为
天中午选择米饭套餐的概率为 .
.
(1)求该同学开学第 天中午选择米饭套餐的概率;
天中午选择米饭套餐的概率;
(2)记该同学开学第 天中午选择米饭套餐的概率为
天中午选择米饭套餐的概率为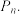 证明:当
证明:当 时,
时, .
.
 天起,每餐只推出即点即取的米饭套餐和面食套餐.某同学每天中午都会在食堂提供的两种套餐中选择一种套餐,若他前
天起,每餐只推出即点即取的米饭套餐和面食套餐.某同学每天中午都会在食堂提供的两种套餐中选择一种套餐,若他前 天选择了米饭套餐,则第
天选择了米饭套餐,则第 天选择米饭套餐的概率为
天选择米饭套餐的概率为 ;若他前
;若他前 天选择了面食套餐,则第
天选择了面食套餐,则第 天选择米饭套餐的概率为
天选择米饭套餐的概率为 .已知他开学第
.已知他开学第 天中午选择米饭套餐的概率为
天中午选择米饭套餐的概率为 .
.(1)求该同学开学第
 天中午选择米饭套餐的概率;
天中午选择米饭套餐的概率;(2)记该同学开学第
 天中午选择米饭套餐的概率为
天中午选择米饭套餐的概率为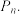 证明:当
证明:当 时,
时, .
.
您最近一年使用:0次
2024-04-13更新
|
2524次组卷
|
5卷引用:重庆市万州第二高级中学2023-2024学年高二下学期期中质量监测数学试题
3 . 已知各项都为正数的数列{an}满足an+2=2an+1+3an.
(1)证明:数列{an+an+1}为等比数列;
(2)若a1= ,a2=
,a2= ,求{an}的通项公式.
,求{an}的通项公式.
(1)证明:数列{an+an+1}为等比数列;
(2)若a1=
 ,a2=
,a2= ,求{an}的通项公式.
,求{an}的通项公式.
您最近一年使用:0次
2022-03-12更新
|
5674次组卷
|
28卷引用:重庆市第七中学校2023-2024学年高二上学期期末模拟数学试题
重庆市第七中学校2023-2024学年高二上学期期末模拟数学试题苏教版(2019) 选修第一册 突围者 第4章 专项拓展训练1北师大版(2019) 选修第二册 突围者 第一章 第三节 等比数列 课时1 等比数列(已下线)第四章 数列(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(苏教版2019选择性必修第一册)(已下线)专题1.2 数列 章末检测2(中)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(人教A版2019选择性必修第二册)2023版 湘教版(2019) 选修第一册 过关斩将 第1章 专题强化练3 数列的递推公式及通项公式(已下线)拓展一:数列递推与通项公式归类(2)河南省郑州市第十八中学2023-2024学年高二上学期期末模拟数学试题(二)(已下线)高二数学第一学期期期末押题密卷05卷2021年1月普通高等学校招生全国统一考试适应性测试(八省联考)数学试题(已下线)专题07 数列(测)-2021年高考数学二轮复习讲练测(文理通用)(已下线)专题07 数列(测)-2021年高考数学二轮复习讲练测(新高考版)(已下线)专题24 数列(解答题)-2021年高考数学(理)二轮复习热点题型精选精练(已下线)专题22 数列(解答题)-2021年高考数学(文)二轮复习热点题型精选精练(已下线)专题23 数列(解答题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)(已下线)第28讲 等比数列及其前n项和(讲)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)专题六 能力提升检测卷 (测) — 2022年高考数学一轮复习讲练测(课标全国版)(已下线)专题26 求数列通项公式必备的方法和技巧-备战2022年高考数学一轮复习一网打尽之重点难点突破江苏省盐城市大丰区新丰中学2021-2022学年高三上学期第二次学情调研数学试题(已下线)一轮巩固卷01-【赢在高考·黄金20卷】备战2022年高考数学模拟卷(新高考专用)(已下线)专题26 数列的通项公式-5甘肃省兰州市第五十八中学2022-2023学年高三上学期第一次模拟考试数学(理科)试题甘肃省兰州市第五十八中学2022-2023学年高三上学期第一次模拟考试数学(文科)试题(已下线)专题6 等比数列的判断(证明)方法 微点1 定义法、等比中项法青海省西宁市海湖中学2023届高三下学期开学考试数学(理)试卷(已下线)专题30 等比数列通项与前n项和(已下线)6.3 等比数列及其前n项和课中·技巧点拨(已下线)第六章 数列6.4 数列的通项公式
名校
4 . 已知等差数列 满足
满足 ,前4项和
,前4项和 .
.
(1)求 的通项公式;
的通项公式;
(2)设等比数列 满足
满足 ,
, ,数列
,数列 的通项公式.
的通项公式.
 满足
满足 ,前4项和
,前4项和 .
.(1)求
 的通项公式;
的通项公式;(2)设等比数列
 满足
满足 ,
, ,数列
,数列 的通项公式.
的通项公式.
您最近一年使用:0次
2022-07-08更新
|
5536次组卷
|
19卷引用:重庆市长寿区2021-2022学年高二下学期期末数学(B)试题
重庆市长寿区2021-2022学年高二下学期期末数学(B)试题重庆市三峡名校联盟2022-2023学年高二上学期12月联考数学试题重庆市为明学校2022-2023学年高二上学期期末数学试题甘肃省张掖市某重点校2022-2023学年高二上学期期中考试数学试题江苏省淮安市马坝高级中学2022-2023学年高二上学期期中数学试题西藏林芝市第二高级中学2022-2023学年高二上学期第一学段考试(期中)数学试题甘肃省白银市第十中学2022-2023学年高二上学期期中考试数学试题广东省人大附中深圳学校2022-2023学年高二上学期期末数学试题陕西省渭南市大荔县2022-2023学年高二上学期期末文科数学试题陕西省渭南市大荔县2022-2023学年高二上学期期末理科数学试题(已下线)模块三 专题7 数列--基础夯实练(北师大2019版 高二)(已下线)模块三 专题6 数列--基础夯实练(人教B版高二)(已下线)高二上学期期末【夯实基础70题考点专练】(选修一+选修二)广东省深圳市高级中学2023届高三上学期第一次调研数学试题北京交通大学附属中学2023届高三上学期10月诊断数学试题四川省遂宁中学校2022-2023学年高三上学期10月月考数学(文)试题四川省遂宁中学校2022-2023学年高三上学期10月月考数学(理)试题辽宁省辽西联合校2022-2023学年高三上学期期中考试数学试题西藏林芝市第二高级中学2024届高三上学期第一次月考数学(理)试题
名校
解题方法
5 . 数列 中,
中, ,
, ,则此数列的通项公式
,则此数列的通项公式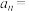
_________ .
 中,
中, ,
, ,则此数列的通项公式
,则此数列的通项公式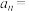
您最近一年使用:0次
2023-03-02更新
|
2169次组卷
|
9卷引用:重庆市荣昌中学校2022-2023学年高二下学期期中数学试题
重庆市荣昌中学校2022-2023学年高二下学期期中数学试题福建省福州市四校联盟(永泰城关中学、连江文笔中学、长乐高级中学、元洪中学)2022-2023学年高二上学期期末联考数学试题广东省佛山市南海区第一中学2022-2023学年高二下学期第一次大测数学试题江西省南昌市第二中学2022-2023学年高二下学期3月月考数学试题(已下线)专题04 数列通项与求和技巧总结(十大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)第06讲 拓展一:数列求通项(7类热点题型讲练)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第二册)(已下线)模块四 期中重组篇(人教B版高二下重庆)江西省南昌市聚仁高级中学2023-2024学年高二下学期第一次月考数学试题(已下线)4.3.1 等比数列的概念——随堂检测
6 . 已知等差数列 和正项等比数列
和正项等比数列 满足:
满足: ,
, ,
,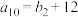 .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)已知数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.
 和正项等比数列
和正项等比数列 满足:
满足: ,
, ,
,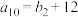 .
.(1)求数列
 ,
, 的通项公式;
的通项公式;(2)已知数列
 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
2024-02-13更新
|
1697次组卷
|
6卷引用:重庆市西南大学附属中学校2023-2024学年2023-2024学年高二下学期3月测试数学试题
重庆市西南大学附属中学校2023-2024学年2023-2024学年高二下学期3月测试数学试题广西百色市2023-2024学年高二上学期期末教学质量调研测试数学试卷甘肃省武威市凉州区2023-2024学年高二下学期开校质量检测数学试卷(已下线)5.3.2 等比数列的前n项和(3知识点+8题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)广东省珠海市香樟中学2023-2024学年高二下学期第一次诊断性监测数学试卷广东省佛山市三水区华侨中学2023-2024学年高二下学期第一次测试数学试卷
7 . 2022年北京冬奥会开幕式中,当《雪花》这个节目开始后,一片巨大的“雪花”呈现在舞台中央,十分壮观.理论上,一片雪花的周长可以无限长,围成雪花的曲线称作“雪花曲线”,又称“科赫曲线”,是瑞典数学家科赫在1904年研究的一种分形曲线.如图是“雪花曲线”的一种形成过程:从一个正三角形开始,把每条边分成三等份,然后以各边的中间一段为底边分别向外作正三角形,再去掉底边,重复进行这一过程

若第1个图中的三角形的周长为1,则第n个图形的周长为___________ ;若第1个图中的三角形的面积为1,则第n个图形的面积为___________ .

若第1个图中的三角形的周长为1,则第n个图形的周长为
您最近一年使用:0次
2022-03-16更新
|
3858次组卷
|
16卷引用:重庆市第八中学校2023-2024学年高二下学期入学适应性训练数学试题
重庆市第八中学校2023-2024学年高二下学期入学适应性训练数学试题江苏省镇江市扬中市第二高级中学2021-2022学年高二下学期3月阶段测试数学试题浙江省杭州学军中学西溪校区2021-2022学年高二下学期4月期中数学试题(已下线)高中数学 高二下-4浙江省金华十校2022-2023学年高二上学期期末模拟数学试题辽宁省大连市庄河市高级中学2022-2023学年高二上学期12月月考数学试题湖北省八市2022届高三下学期3月联考数学试题(已下线)专题20 科赫曲线(已下线)考点15 数列综合问题-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)天津市耀华中学2022-2023学年高三上学期统练(二)数学试题福建省福州第八中学2023届高三上学期质检四数学试题山西省朔州市怀仁市2023届高三二模数学试题(已下线)专题05 数列(已下线)押新高考第16题 数列性质及其应用(已下线)专题10 数列通项公式的求法 微点2 累加法(已下线)数列的综合应用
名校
解题方法
8 . 已知数列 的前n项和为
的前n项和为 ,且满足
,且满足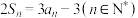 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设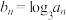 ,数列
,数列 的前n项和为
的前n项和为 ,求证
,求证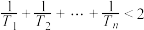 .
.
 的前n项和为
的前n项和为 ,且满足
,且满足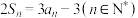 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
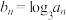 ,数列
,数列 的前n项和为
的前n项和为 ,求证
,求证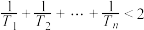 .
.
您最近一年使用:0次
2024-03-21更新
|
1404次组卷
|
3卷引用:重庆市巴蜀中学校2023-2024学年高二下学期第一次月考数学试卷
名校
9 . 已知一个蜂巢里有1只蜜蜂,第1天,它飞出去找回了4个伙伴;第2天,5只蜜蜂飞出去,各自找回了4个伙伴,……按照这个规律继续下去,第20天所有的蜜蜂都归巢后,蜂巢中一共有蜜蜂( )
| A.420只 | B.520只 | C. 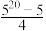 只 只 | D.  只 只 |
您最近一年使用:0次
2022-05-31更新
|
3058次组卷
|
15卷引用:重庆市巫山县官渡中学2021-2022学年高二下学期期末数学试题
重庆市巫山县官渡中学2021-2022学年高二下学期期末数学试题辽宁师范大学附属中学2021-2022学年高二下学期5月模块考试数学试题单元综合测试-数列(已下线)4.3.1 等比数列的概念(第2课时)(分层作业)江西省吉安市第一中学2022-2023学年高二下学期第一次段考数学试题(已下线)第4讲 等比数列的通项及性质5大题型总结(3)(已下线)4.3.1 等比数列的概念(1)1.3.1 等比数列及其通项公式(同步练习)(已下线)专题05 等比数列与数列综合求和-2023-2024学年高二数学期末复习重难培优与单元检测(人教A版2019)(已下线)1.3.1 等比数列7种常见考法归类(2)(已下线)1.3.1 等比数列7种常见考法归类(2)湖南省邵阳市海谊中学2023-2024学年高二上学期11月期中考试数学试题(已下线)第03讲 等比数列及其前n项和 (讲)-2023年高考数学一轮复习讲练测(新教材新高考)(已下线)专题25 等比数列及其前n项和-1第十三届高一试题(B卷)-“枫叶新希望杯”全国数学大赛真题解析(高中版)
10 . 已知数列 的前n项和为
的前n项和为 ,且
,且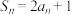 .
.
(1)求数列 的通项公式
的通项公式 ;
;
(2)若 ,求n.
,求n.
 的前n项和为
的前n项和为 ,且
,且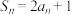 .
.(1)求数列
 的通项公式
的通项公式 ;
;(2)若
 ,求n.
,求n.
您最近一年使用:0次
2021-05-24更新
|
5127次组卷
|
16卷引用:重庆市缙云教育联盟2020-2021学年高二下学期期末数学试题
重庆市缙云教育联盟2020-2021学年高二下学期期末数学试题重庆市铜梁一中等三校2022-2023学年高二上学期期末数学试题(已下线)本册综合卷(能力提升)-2020-2021学年高二数学单元测试定心卷(人教B版2019选择性必修第三册)江西省新余市第四中学2021-2022学年高二上学期第一次月考数学(文)试题(已下线)4.1数列(A 基础培优练)-2021-2022学年高二数学同步双培优检测(苏教版2019选择性必修第一册)福建省龙岩第一中学2021-2022学年高二上学期模块考试(期中)数学试题河南省驻马店市第二高级中学2021-2022学年高二上学期第一次月考(文、理)数学试题河南省周口市西华县第三高级中学2023-2024学年高二上学期第三次月考数学试题四川省天府名校2021届高三5月诊断性考试文科数学试题四川省天府名校2021届高三5月诊断性考试理科数学试题西藏自治区林芝市第二高级中学2022届高三上学期第一次月考数学(理)试题(已下线)2021年高考全国乙卷数学(理)高考真题变式题16-20题(已下线)解密08 数列(分层训练)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)(已下线)2021年高考全国乙卷数学(理)高考真题变式题16-20题四川省邻水县第二中学2021-2022学年高三上学期9月月考数学理科试题吉林省白城市通榆县毓才高级中学2023-2024学年高三上学期9月月考数学试题



