名校
1 . 已知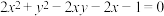 .若
.若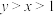 ,求
,求 的最大值为
的最大值为______ ;若 且
且 ,求
,求 的最大值为
的最大值为______ .
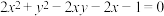 .若
.若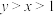 ,求
,求 的最大值为
的最大值为 且
且 ,求
,求 的最大值为
的最大值为
您最近一年使用:0次
名校
解题方法
2 . 已知函数 是定义在
是定义在 上的奇函数,若
上的奇函数,若 ,且
,且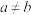 ,都有
,都有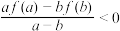 成立,则不等式
成立,则不等式 的解集为( )
的解集为( )
 是定义在
是定义在 上的奇函数,若
上的奇函数,若 ,且
,且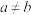 ,都有
,都有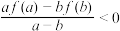 成立,则不等式
成立,则不等式 的解集为( )
的解集为( )A. | B.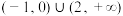 |
C. | D.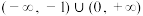 |
您最近一年使用:0次
2024-03-25更新
|
1032次组卷
|
3卷引用:3.2.2函数奇偶性
3 . 已知不等式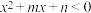 的解集为
的解集为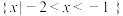 ,函数
,函数 (
( ,且
,且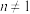 ),
), (
( ,且
,且 ).
).
(1)求不等式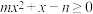 的解集;
的解集;
(2)若对于任意的 ,均存在
,均存在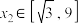 ,满足
,满足 ,求实数
,求实数 的取值范围.
的取值范围.
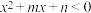 的解集为
的解集为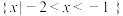 ,函数
,函数 (
( ,且
,且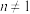 ),
), (
( ,且
,且 ).
).(1)求不等式
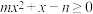 的解集;
的解集;(2)若对于任意的
 ,均存在
,均存在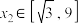 ,满足
,满足 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
4 . 已知 ,且
,且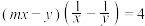 ,则
,则 的最小值为
的最小值为__________ .
 ,且
,且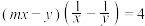 ,则
,则 的最小值为
的最小值为
您最近一年使用:0次
2024-01-17更新
|
1072次组卷
|
4卷引用:辽宁省县级重点高中协作体2023-2024学年高一上学期末考试数学试题
名校
解题方法
5 . 已知函数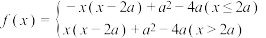 ,
, .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)如果关于 的方程
的方程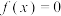 有三个不相等的非零实数解
有三个不相等的非零实数解 ,
, ,
, ,求
,求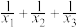 的取值范围.
的取值范围.
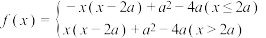 ,
, .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)如果关于
 的方程
的方程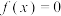 有三个不相等的非零实数解
有三个不相等的非零实数解 ,
, ,
, ,求
,求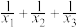 的取值范围.
的取值范围.
您最近一年使用:0次
名校
6 . 已知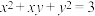 ,下列说法正确的有( )
,下列说法正确的有( )
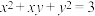 ,下列说法正确的有( )
,下列说法正确的有( )A. 的取值范围是 的取值范围是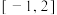 |
B. 的取值范围是 的取值范围是 |
C.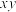 的取值范围是 的取值范围是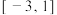 |
D.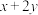 的取值范围是 的取值范围是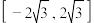 |
您最近一年使用:0次
2023-12-11更新
|
1250次组卷
|
4卷引用:辽宁省沈阳市辽宁省实验中学2023-2024学年高一上学期12月月考数学试题
名校
解题方法
7 . 已知 是定义在
是定义在 上的奇函数,满足
上的奇函数,满足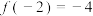 ,且当
,且当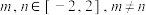 时,有
时,有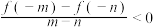 .
.
(1)判断函数 的单调性;
的单调性;
(2)解不等式: ;
;
(3)若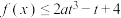 对所有
对所有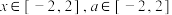 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 是定义在
是定义在 上的奇函数,满足
上的奇函数,满足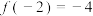 ,且当
,且当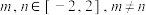 时,有
时,有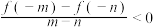 .
.(1)判断函数
 的单调性;
的单调性;(2)解不等式:
 ;
;(3)若
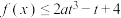 对所有
对所有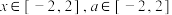 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-06更新
|
1343次组卷
|
8卷引用:河南省新高中联盟TOP二十名校2023-2024学年高一上学期12月调研考试数学试题
河南省新高中联盟TOP二十名校2023-2024学年高一上学期12月调研考试数学试题江苏省镇江市扬中市第二高级中学2023-2024高一上学期12月数学调查试卷(已下线)专题04 函数的性质与应用2-期末复习重难培优与单元检测(人教A版2019)山西省忻州市忻州实验中学校2023-2024学年高一下学期第二次数学拉练试题安徽省太和中学2023-2024学年高一下学期第一次教学质量检测数学试题内蒙古鄂尔多斯市西四旗2024-2025学年高一上学期期中考试数学试题(已下线)专题2.2 函数的单调性、奇偶性、对称性与周期性【九大题型】江西省鹰潭市余江区第一中学2024-2025学年高一上学期10月期中数学试题
名校
解题方法
8 . 已知函数 和
和 ,定义集合
,定义集合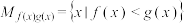 .
.
(1)设 ,求
,求 ;
;
(2)设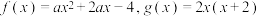 ,当
,当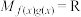 时,求
时,求 的取值范围;
的取值范围;
(3)设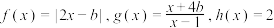 ,若
,若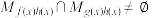 ,求
,求 的取值范围.
的取值范围.
 和
和 ,定义集合
,定义集合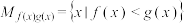 .
.(1)设
 ,求
,求 ;
;(2)设
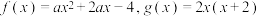 ,当
,当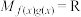 时,求
时,求 的取值范围;
的取值范围;(3)设
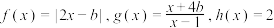 ,若
,若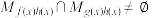 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-03更新
|
1288次组卷
|
3卷引用:山东省滨州市北镇中学2023-2024学年高一上学期第一届高中学科素养知识竞赛数学试题
解题方法
9 . 定义在R上的函数 ,对任意x,
,对任意x,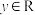 都有
都有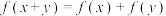 ,且当
,且当 时,
时, .
.
(1)求证: 为奇函数;
为奇函数;
(2)求证: 为R上的增函数;
为R上的增函数;
(3)已知 解关于x的不等式
解关于x的不等式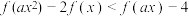 ,
,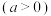 .
.
 ,对任意x,
,对任意x,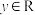 都有
都有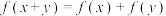 ,且当
,且当 时,
时, .
.(1)求证:
 为奇函数;
为奇函数;(2)求证:
 为R上的增函数;
为R上的增函数;(3)已知
 解关于x的不等式
解关于x的不等式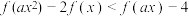 ,
,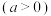 .
.
您最近一年使用:0次
10 . 定义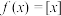 (其中
(其中 表示不小于
表示不小于 的最小整数)为“向上取整函数”,例如
的最小整数)为“向上取整函数”,例如 ,
,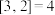 ,
, .以下描述正确的是( )
.以下描述正确的是( )
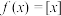 (其中
(其中 表示不小于
表示不小于 的最小整数)为“向上取整函数”,例如
的最小整数)为“向上取整函数”,例如 ,
,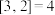 ,
, .以下描述正确的是( )
.以下描述正确的是( )A.若 ,则 ,则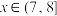 | B.若 ,则 ,则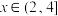 |
C.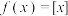 是定义在 是定义在 上的奇函数 上的奇函数 | D.若 ,则 ,则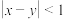 |
您最近一年使用:0次
2023-11-28更新
|
247次组卷
|
3卷引用:辽宁省县级重点高中协作体2023-2024学年高一上学期期中考试数学试题
辽宁省县级重点高中协作体2023-2024学年高一上学期期中考试数学试题河南省郑州市第四十四高级中学2023-2024学年高一上学期期中数学试题(已下线)专题3 不等式性质与不等关系的应用【练】(高一期中压轴专项)



