名校
1 . 圆柱的底面半径为1,侧面积为 ,则该圆柱外接球的表面积为
,则该圆柱外接球的表面积为______ .
 ,则该圆柱外接球的表面积为
,则该圆柱外接球的表面积为
您最近一年使用:0次
2024-09-01更新
|
132次组卷
|
10卷引用:上海市浦东新区上海实验学校2024届高三下学期2月测验数学试卷
上海市浦东新区上海实验学校2024届高三下学期2月测验数学试卷上海市宝山中学2023-2024学年高二下学期3月考数学试卷(已下线)专题10 球- 【暑假自学课】(沪教版2020)(已下线)重难点突破01 玩转外接球、内切球、棱切球(二十四大题型)-1(已下线)专题15 简单几何体的表面积与体积-《重难点题型·高分突破》(人教A版2019必修第二册)(已下线)重难点08 玩转外接球、内切球、棱切球经典问题-【帮课堂】(苏教版2019必修第二册)(已下线)第十一章:立体几何初步章末重点题型复习(1)-同步精品课堂(人教B版2019必修第四册)(已下线)专题21 空间图形的表面积和体积-《重难点题型·高分突破》(苏教版2019必修第二册)山东省淄博市高青县第一中学2024-2025学年高二二部上学期开学测试数学试题广东省三校2024-2025学年高二上学期第一次质量检测数学试题
名校
2 . 棱长为 的正方体
的正方体 中,
中, 为棱
为棱 的中点,
的中点, 为正方形
为正方形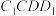 内一个动点(包括边界),且
内一个动点(包括边界),且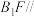 平面
平面 ,则当三棱锥
,则当三棱锥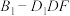 体积取最大时,其外接球的表面积为
体积取最大时,其外接球的表面积为_________ .
 的正方体
的正方体 中,
中, 为棱
为棱 的中点,
的中点, 为正方形
为正方形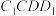 内一个动点(包括边界),且
内一个动点(包括边界),且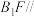 平面
平面 ,则当三棱锥
,则当三棱锥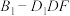 体积取最大时,其外接球的表面积为
体积取最大时,其外接球的表面积为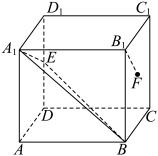
您最近一年使用:0次
名校
解题方法
3 . 三棱锥 各顶点均在半径为
各顶点均在半径为 的球
的球 的表面上,
的表面上,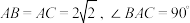 ,二面角
,二面角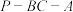 的大小为
的大小为 ,则对以下两个命题,判断正确的是( )
,则对以下两个命题,判断正确的是( )
①三棱锥 的体积为
的体积为 ;②点
;②点 形成的轨迹长度为
形成的轨迹长度为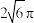 .
.
 各顶点均在半径为
各顶点均在半径为 的球
的球 的表面上,
的表面上,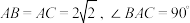 ,二面角
,二面角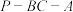 的大小为
的大小为 ,则对以下两个命题,判断正确的是( )
,则对以下两个命题,判断正确的是( )①三棱锥
 的体积为
的体积为 ;②点
;②点 形成的轨迹长度为
形成的轨迹长度为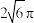 .
.| A.①②都是真命题 |
| B.①是真命题,②是假命题 |
| C.①是假命题,②是真命题 |
| D.①②都是假命题 |
您最近一年使用:0次
2024高三·上海·专题练习
解题方法
4 . 已知正方体 的棱长为2,动点
的棱长为2,动点 在正方形
在正方形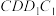 内,则下列正确命题的序号是
内,则下列正确命题的序号是
①若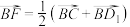 ,则三棱锥的
,则三棱锥的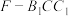 的外接球表面积为
的外接球表面积为
②若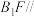 平面
平面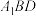 ,则
,则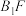 不可能垂直
不可能垂直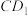
③若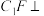 平面
平面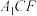 ,则点
,则点 的位置唯一
的位置唯一
④若点 为
为 中点,则三棱锥
中点,则三棱锥 的体积是三棱锥
的体积是三棱锥 体积的一半
体积的一半
您最近一年使用:0次
名校
解题方法
5 . 已知正四棱锥的底面边长为4,其各顶点都在同一球面上,若该球的表面积为 ,则四棱锥的最大体积为
,则四棱锥的最大体积为______ .
 ,则四棱锥的最大体积为
,则四棱锥的最大体积为
您最近一年使用:0次
2024-03-14更新
|
1370次组卷
|
4卷引用:上海市进才中学2023-2024学年高三下学期3月月考数学试卷
上海市进才中学2023-2024学年高三下学期3月月考数学试卷湖南省长沙市长郡中学2023-2024学年高一下学期4月选科适应性检测数学试题(已下线)专题3.9 立体中的外接球和内切球-重难点突破及混淆易错规避(人教A版2019必修第二册)专题训练:与球有关的外接和内切问题小题精练30题-同步题型分类归纳讲与练(人教A版2019必修第二册)
名校
解题方法
6 . 已知一个正四面体的棱长为4,则其外接球与以其一个顶点为球心,2为半径的球面所形成的交线的长度为______ .
您最近一年使用:0次
名校
解题方法
7 . 已知正四面体 的边长为
的边长为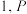 是空间一点,若
是空间一点,若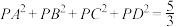 ,则
,则 的最小值为
的最小值为__________ .
 的边长为
的边长为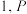 是空间一点,若
是空间一点,若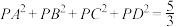 ,则
,则 的最小值为
的最小值为
您最近一年使用:0次
2024-02-27更新
|
1060次组卷
|
4卷引用:上海市青浦高级中学2023-2024学年高三下学期5月质量检测数学试卷
上海市青浦高级中学2023-2024学年高三下学期5月质量检测数学试卷浙江省七彩阳光联联盟2023-2024学年高三下学期开学考试数学试题(已下线)第3套-期初重组模拟卷(已下线)第11题 莱布尼兹定理背景下的解三角形最值问题(一题多解)
解题方法
8 . 对于一个三维空间,如果一个平面与一个球只有一个交点,则称这个平面是这个球的切平面.已知在空间直角坐标系 中,球
中,球 的半径为
的半径为 ,记平面
,记平面 、平面
、平面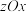 、平面
、平面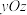 分别为
分别为 、
、 、
、 .
.
(1)若棱长为 的正方体、棱长为
的正方体、棱长为 的正四面体的内切球均为球
的正四面体的内切球均为球 ,求
,求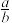 的值;
的值;
(2)若球 在
在 处有一切平面为
处有一切平面为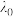 ,求
,求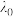 与
与 的交线方程,并写出它的一个法向量;
的交线方程,并写出它的一个法向量;
(3)如果在球面上任意一点作切平面 ,记
,记 与
与 、
、 、
、 的交线分别为
的交线分别为 、
、 、
、 ,求
,求 到
到 、
、 、
、 距离乘积的最小值.
距离乘积的最小值.
 中,球
中,球 的半径为
的半径为 ,记平面
,记平面 、平面
、平面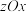 、平面
、平面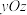 分别为
分别为 、
、 、
、 .
.(1)若棱长为
 的正方体、棱长为
的正方体、棱长为 的正四面体的内切球均为球
的正四面体的内切球均为球 ,求
,求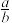 的值;
的值;(2)若球
 在
在 处有一切平面为
处有一切平面为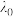 ,求
,求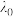 与
与 的交线方程,并写出它的一个法向量;
的交线方程,并写出它的一个法向量;(3)如果在球面上任意一点作切平面
 ,记
,记 与
与 、
、 、
、 的交线分别为
的交线分别为 、
、 、
、 ,求
,求 到
到 、
、 、
、 距离乘积的最小值.
距离乘积的最小值.
您最近一年使用:0次
2024-01-14更新
|
883次组卷
|
6卷引用:上海市普陀区桃浦中学2024届高三上学期期末数学试题
上海市普陀区桃浦中学2024届高三上学期期末数学试题(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)(已下线)第二章 立体几何中的计算 专题六 几何体的外接球、棱切球、内切球 微点15 几何体的内切球与棱切球(一)【基础版】(已下线)第七章 应用空间向量解立体几何问题拓展 专题二 平面法向量求法及其应用 微点2 平面法向量求法及其应用(二)【培优版】(已下线)专题4 立体几何中的新定义压轴大题(二)【讲】(已下线)专题5 解析几何中的新定义压轴大题(二)【讲】
解题方法
9 . 棱台 中,
中,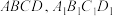 是两个菱形,
是两个菱形, ,
, ,
,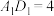 ,高为5,有一个球O,使得此棱台能在此球内任意转动,求此球O半径的最小值
,高为5,有一个球O,使得此棱台能在此球内任意转动,求此球O半径的最小值____________ (保留3位有效数字)
 中,
中,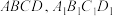 是两个菱形,
是两个菱形, ,
, ,
,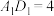 ,高为5,有一个球O,使得此棱台能在此球内任意转动,求此球O半径的最小值
,高为5,有一个球O,使得此棱台能在此球内任意转动,求此球O半径的最小值
您最近一年使用:0次
名校
解题方法
10 . 在化学知识中,空间利用率是指构成晶体的原子在整个晶体空间中所占有的体积之比,即空间利用率 晶胞含有原子的体积
晶胞含有原子的体积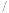 晶胞体积.如图是某金属晶体晶胞的一种堆积方式——体心立方堆积,该堆积方式是以正方体8个顶点为球心的球互不相切,但均与以正方体体心为球心的球相切.晶胞为上述正方体,则该金属晶体晶胞的空间利用率为
晶胞体积.如图是某金属晶体晶胞的一种堆积方式——体心立方堆积,该堆积方式是以正方体8个顶点为球心的球互不相切,但均与以正方体体心为球心的球相切.晶胞为上述正方体,则该金属晶体晶胞的空间利用率为__________ .
 晶胞含有原子的体积
晶胞含有原子的体积 晶胞体积.如图是某金属晶体晶胞的一种堆积方式——体心立方堆积,该堆积方式是以正方体8个顶点为球心的球互不相切,但均与以正方体体心为球心的球相切.晶胞为上述正方体,则该金属晶体晶胞的空间利用率为
晶胞体积.如图是某金属晶体晶胞的一种堆积方式——体心立方堆积,该堆积方式是以正方体8个顶点为球心的球互不相切,但均与以正方体体心为球心的球相切.晶胞为上述正方体,则该金属晶体晶胞的空间利用率为
您最近一年使用:0次
2023-12-21更新
|
323次组卷
|
2卷引用:上海市宝山区吴淞中学2024届高三下学期3月月考数学试题



