名校
解题方法
1 . 平面内与两定点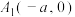 ,
,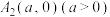 连线的斜率之积等于非零常数m的点的轨迹,加上
连线的斜率之积等于非零常数m的点的轨迹,加上 ,
, 两点所成的曲线记为曲线C.
两点所成的曲线记为曲线C.
(1)求曲线C的方程,并讨论C的形状与m值的关系;
(2)若 时,对应的曲线为
时,对应的曲线为 ;对给定的
;对给定的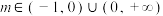 ,对应的曲线为
,对应的曲线为 .设
.设 ,
, 是
是 的两个焦点,试问:在
的两个焦点,试问:在 上是否存在点N,使得
上是否存在点N,使得 的面积
的面积 ,并证明你的结论.
,并证明你的结论.
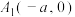 ,
,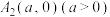 连线的斜率之积等于非零常数m的点的轨迹,加上
连线的斜率之积等于非零常数m的点的轨迹,加上 ,
, 两点所成的曲线记为曲线C.
两点所成的曲线记为曲线C.(1)求曲线C的方程,并讨论C的形状与m值的关系;
(2)若
 时,对应的曲线为
时,对应的曲线为 ;对给定的
;对给定的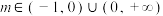 ,对应的曲线为
,对应的曲线为 .设
.设 ,
, 是
是 的两个焦点,试问:在
的两个焦点,试问:在 上是否存在点N,使得
上是否存在点N,使得 的面积
的面积 ,并证明你的结论.
,并证明你的结论.
您最近一年使用:0次
2023-07-06更新
|
229次组卷
|
2卷引用:江西省上饶市第一中学2023-2024学年高二上学期第一次月考(10月)数学试题
2 . 已知双曲线 的左、右焦点分别为
的左、右焦点分别为 、
、 ,左、右顶点分别为
,左、右顶点分别为 、
、 ,
, 为双曲线右支上的一点,且直线
为双曲线右支上的一点,且直线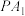 与
与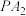 的斜率之积等于
的斜率之积等于 ,则下列说法正确的是( )
,则下列说法正确的是( )
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,左、右顶点分别为
,左、右顶点分别为 、
、 ,
, 为双曲线右支上的一点,且直线
为双曲线右支上的一点,且直线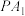 与
与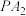 的斜率之积等于
的斜率之积等于 ,则下列说法正确的是( )
,则下列说法正确的是( )A.双曲线 的渐近线方程为 的渐近线方程为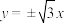 |
B.若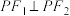 ,且 ,且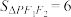 ,则 ,则 |
C.分别以线段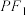 、 、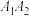 为直径的两个圆内切 为直径的两个圆内切 |
D.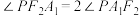 |
您最近一年使用:0次
2023-07-06更新
|
689次组卷
|
5卷引用:四川省南充市仪陇中学校2023-2024学年高二上学期12月月考数学试题
四川省南充市仪陇中学校2023-2024学年高二上学期12月月考数学试题广东省广州市天河区2022-2023学年高二下学期期末数学试题(已下线)模块三 专题11 双曲线 B能力卷(已下线)模块三 专题14 双曲线 B能力卷广东省揭阳市普宁市2023-2024学年高二上学期期末数学试题
名校
解题方法
3 . 已知双曲线 :
: 的离心率为
的离心率为 ,且过
,且过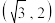 .
.
(1)求双曲线 的方程;
的方程;
(2)若直线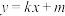 与双曲线
与双曲线 交于
交于 两点,
两点, 是
是 的右顶点,且直线
的右顶点,且直线 与
与 的斜率之积为
的斜率之积为 ,证明:直线
,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
 :
: 的离心率为
的离心率为 ,且过
,且过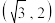 .
.(1)求双曲线
 的方程;
的方程;(2)若直线
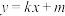 与双曲线
与双曲线 交于
交于 两点,
两点, 是
是 的右顶点,且直线
的右顶点,且直线 与
与 的斜率之积为
的斜率之积为 ,证明:直线
,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
您最近一年使用:0次
2023-06-27更新
|
1145次组卷
|
8卷引用:重庆市三峡名校联盟2023-2024学年高二上学期联考数学试卷
重庆市三峡名校联盟2023-2024学年高二上学期联考数学试卷山东省临沂市临沭第一中学2023-2024学年高二上学期第二次教学质量检测数学试题新疆维吾尔自治区阿克苏地库车市第二中学2023-2024学年高二上学期第二次月考(12月)数学浙江省杭州市六县九校联盟2022-2023学年高二下学期期中数学试题(已下线)第22讲 双曲线的简单几何性质9种常见考法归类(3)(已下线)第11讲 拓展五:圆锥曲线的方程(定值问题)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第一册)(已下线)专题3.9 圆锥曲线中的定点、定值、定直线问题大题专项训练【九大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)专题02 期中真题精选(压轴93题10类考点专练)(3)
解题方法
4 . 已知双曲线 :
: 的左、右顶点分别为
的左、右顶点分别为 ,
, ,且顶点到渐近线的距离为
,且顶点到渐近线的距离为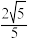 ,点
,点 是双曲线
是双曲线 右支上一动点(不与
右支上一动点(不与 重合),且满足
重合),且满足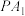 ,
,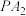 的斜率之积为
的斜率之积为 .
.
(1)求双曲线 的方程.
的方程.
(2)过点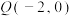 的直线
的直线 与双曲线
与双曲线 交于
交于 轴上方的
轴上方的 ,
, 两点,若
两点,若 是线段
是线段 的中点,
的中点, 是线段
是线段 上一点,且
上一点,且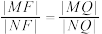 ,
, 为坐标原点,试判断直线
为坐标原点,试判断直线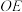 ,
, 的斜率之积是否为定值.若为定值,求出该定值;若不是,请说明理由.
的斜率之积是否为定值.若为定值,求出该定值;若不是,请说明理由.
 :
: 的左、右顶点分别为
的左、右顶点分别为 ,
, ,且顶点到渐近线的距离为
,且顶点到渐近线的距离为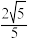 ,点
,点 是双曲线
是双曲线 右支上一动点(不与
右支上一动点(不与 重合),且满足
重合),且满足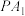 ,
,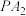 的斜率之积为
的斜率之积为 .
.(1)求双曲线
 的方程.
的方程.(2)过点
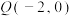 的直线
的直线 与双曲线
与双曲线 交于
交于 轴上方的
轴上方的 ,
, 两点,若
两点,若 是线段
是线段 的中点,
的中点, 是线段
是线段 上一点,且
上一点,且 ,
, 为坐标原点,试判断直线
为坐标原点,试判断直线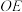 ,
, 的斜率之积是否为定值.若为定值,求出该定值;若不是,请说明理由.
的斜率之积是否为定值.若为定值,求出该定值;若不是,请说明理由.
您最近一年使用:0次
2023-06-20更新
|
365次组卷
|
4卷引用:山西省吕梁市孝义市2022-2023学年高二下学期5月联考数学试题
名校
解题方法
5 . 已知双曲线 经过点
经过点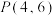 ,且离心率为2.
,且离心率为2.
(1)求 的方程;
的方程;
(2)过点 作
作 轴的垂线,交直线
轴的垂线,交直线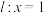 于点
于点 ,交
,交 轴于点
轴于点 .设点
.设点 为双曲线
为双曲线 上的两个动点,直线
上的两个动点,直线 的斜率分别为
的斜率分别为 ,若
,若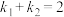 ,求
,求 .
.
 经过点
经过点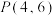 ,且离心率为2.
,且离心率为2.(1)求
 的方程;
的方程;(2)过点
 作
作 轴的垂线,交直线
轴的垂线,交直线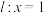 于点
于点 ,交
,交 轴于点
轴于点 .设点
.设点 为双曲线
为双曲线 上的两个动点,直线
上的两个动点,直线 的斜率分别为
的斜率分别为 ,若
,若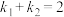 ,求
,求 .
.
您最近一年使用:0次
2023-06-18更新
|
1743次组卷
|
9卷引用:江苏省四所百强中学(南京师大附中等)2022-2023学年高二下学期6月月考数学试题
江苏省四所百强中学(南京师大附中等)2022-2023学年高二下学期6月月考数学试题江苏省镇江市句容高级中学2023-2024学年高二上学期10月强基班学情调查数学试题新疆维吾尔自治区石河子市第一中学2023-2024学年高二上学期12月月考数学试题江苏省南京师范大学附属中学2022-2023学年高二下学期期末数学试题江西省宜春市宜丰县宜丰中学2024届高三上学期12月月考数学试题江苏省苏州市相城区陆慕高级中学2024届高三上学期12月阶段性教学质量调研测试数学试题河南省郑州市宇华实验学校2024届高三上学期12月月考数学试题江苏省南京市六校联合体2023-2024学年高三上学期11月期中数学试题(已下线)江苏省南京市六校联合体2023-2024学年高三上学期11月期中数学试题变式题19-22
名校
解题方法
6 . 已知直线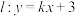 与双曲线
与双曲线 的右支交于不同的两点
的右支交于不同的两点 和
和 ,与
,与 轴交于点
轴交于点 ,且直线
,且直线 上存在一点
上存在一点 满足
满足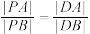 (
( 不与
不与 重合).
重合).
(1)求实数 的取值范围;
的取值范围;
(2)证明:当 变化时,点
变化时,点 的纵坐标为定值.
的纵坐标为定值.
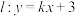 与双曲线
与双曲线 的右支交于不同的两点
的右支交于不同的两点 和
和 ,与
,与 轴交于点
轴交于点 ,且直线
,且直线 上存在一点
上存在一点 满足
满足 (
( 不与
不与 重合).
重合).(1)求实数
 的取值范围;
的取值范围;(2)证明:当
 变化时,点
变化时,点 的纵坐标为定值.
的纵坐标为定值.
您最近一年使用:0次
2023-05-29更新
|
223次组卷
|
2卷引用:河南省部分重点中学2022-2023学年高二下学期5月质量检测数学试题
解题方法
7 . 已知双曲线 经过点
经过点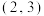 ,一条渐近线方程为
,一条渐近线方程为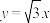 ,直线
,直线 交双曲线于
交双曲线于 两点.
两点.
(1)求双曲线 的方程.
的方程.
(2)若 过双曲线的右焦点
过双曲线的右焦点 ,是否存在
,是否存在 轴上的点
轴上的点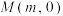 ,使得直线
,使得直线 绕点
绕点 无论怎样转动,都有
无论怎样转动,都有 成立?若存在,求实数
成立?若存在,求实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 经过点
经过点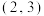 ,一条渐近线方程为
,一条渐近线方程为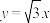 ,直线
,直线 交双曲线于
交双曲线于 两点.
两点.(1)求双曲线
 的方程.
的方程.(2)若
 过双曲线的右焦点
过双曲线的右焦点 ,是否存在
,是否存在 轴上的点
轴上的点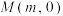 ,使得直线
,使得直线 绕点
绕点 无论怎样转动,都有
无论怎样转动,都有 成立?若存在,求实数
成立?若存在,求实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2023-10-16更新
|
1027次组卷
|
5卷引用:广东省深圳市深圳大学附属实验中学2022-2023学年高二上学期12月段考数学试题
广东省深圳市深圳大学附属实验中学2022-2023学年高二上学期12月段考数学试题贵州省铜仁市松桃苗族自治县群希高级中学2023-2024学年高二上学期第三次月考数学试题(已下线)专题08 椭圆双曲线综合大题(9题型)-【巅峰课堂】2023-2024学年高二数学上学期期中期末复习讲练测(人教A版2019选择性必修第一册)重庆市渝南田家炳中学校2023-2024学年高二上学期半期考试数学试题(已下线)考点19 解析几何中的探索性问题 2024届高考数学考点总动员
8 . 已知点P为双曲线 上任意一点,
上任意一点,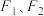 为其左、右焦点,O为坐标原点.过点P向双曲线两渐近线作垂线,设垂足分别为M、N,则下列所述正确的是( )
为其左、右焦点,O为坐标原点.过点P向双曲线两渐近线作垂线,设垂足分别为M、N,则下列所述正确的是( )
 上任意一点,
上任意一点,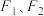 为其左、右焦点,O为坐标原点.过点P向双曲线两渐近线作垂线,设垂足分别为M、N,则下列所述正确的是( )
为其左、右焦点,O为坐标原点.过点P向双曲线两渐近线作垂线,设垂足分别为M、N,则下列所述正确的是( )A. 为定值 为定值 | B.O、P、M、N四点一定共圆 |
C.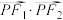 的最小值为 的最小值为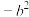 | D.存在点P满足P、M、 三点共线时,P、N、 三点共线时,P、N、 三点也共线 三点也共线 |
您最近一年使用:0次
2023-05-01更新
|
1073次组卷
|
2卷引用:重庆市黔江中学校2023-2024学年高二上学期12月月考数学试卷
名校
解题方法
9 . 已知双曲线 的离心率为
的离心率为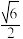 ,点
,点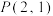 在双曲线
在双曲线 上.
上.
(1)求双曲线
 的方程;
的方程;(2)设过点
 的直线
的直线 与曲线
与曲线 交于
交于 两点,问在
两点,问在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得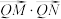 为常数?若存在,求出
为常数?若存在,求出 点坐标及此常数的值,若不存在,说明理由.
点坐标及此常数的值,若不存在,说明理由.
您最近一年使用:0次
2023-08-10更新
|
721次组卷
|
6卷引用:江苏省如东一中、徐州中学、宿迁一中2023-2024学年高二上学期10月阶段性联考数学试题
江苏省如东一中、徐州中学、宿迁一中2023-2024学年高二上学期10月阶段性联考数学试题江苏省盐城市射阳中学2023-2024学年高二上学期10月月考数学试题江苏省徐州市铜山区2022-2023学年高二上学期期中数学试题(已下线)高二数学上学期期中考模拟卷(直线与方程+圆与方程+圆锥曲线与方程)-【考点通关】2023-2024学年高二数学高频考点与解题策略(苏教版2019选择性必修第一册)(已下线)通关练16 双曲线13考点精练(100题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)(已下线)重难专攻(十)圆锥曲线中的定点问题 讲
10 . 已知双曲线 的右焦点为
的右焦点为 ,左、右顶点分别为
,左、右顶点分别为 、
、 ,点
,点 是双曲线
是双曲线 上异于左、右顶点的一点,则下列说法正确的是( )
上异于左、右顶点的一点,则下列说法正确的是( )
A.过点 有且仅有 有且仅有 条直线与双曲线 条直线与双曲线 有且仅有一个交点 有且仅有一个交点 |
B.点 关于双曲线 关于双曲线 的渐近线的对称点在双曲线 的渐近线的对称点在双曲线 上 上 |
C.若直线 、 、 的斜率分别为 的斜率分别为 、 、 ,则 ,则 |
D.过点 的直线与双曲线 的直线与双曲线 交于 交于 、 、 两点,则 两点,则 的最小值为 的最小值为 |
您最近一年使用:0次
2023-03-16更新
|
256次组卷
|
5卷引用:山西省晋中市介休市第一中学校2022-2023学年高二下学期3月月考数学试题



