2025高三·全国·专题练习
解题方法
1 . 抛物线 的焦点为
的焦点为 ,准线为直线
,准线为直线 ,过点
,过点 的直线交抛物线于
的直线交抛物线于 ,
, 两点,分别过
两点,分别过 ,
, 作抛物线的切线交于点
作抛物线的切线交于点 ,
,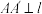 于点
于点 ,
,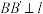 于点
于点 ,则说法错误的是( )
,则说法错误的是( )
 的焦点为
的焦点为 ,准线为直线
,准线为直线 ,过点
,过点 的直线交抛物线于
的直线交抛物线于 ,
, 两点,分别过
两点,分别过 ,
, 作抛物线的切线交于点
作抛物线的切线交于点 ,
,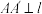 于点
于点 ,
,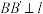 于点
于点 ,则说法错误的是( )
,则说法错误的是( )A.点 在直线 在直线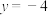 上 上 | B.点 在直线 在直线 上的投影是定点 上的投影是定点 |
C.以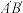 为直径的圆与直线 为直径的圆与直线 相切 相切 | D. 的最小值为 的最小值为 |
您最近一年使用:0次
2 . 已知抛物线 的焦点为
的焦点为 ,过点
,过点 的直线
的直线 与抛物线相交于
与抛物线相交于 ,
, 两点,线段
两点,线段 的中点为
的中点为 .过点
.过点 ,
, 分别向
分别向 的准线作垂线,垂足分别为点
的准线作垂线,垂足分别为点 ,
, ,过点
,过点 向
向 的准线作垂线,交抛物线于点
的准线作垂线,交抛物线于点 ,交准线于点
,交准线于点 ,
, 为坐标原点,则( )
为坐标原点,则( )
 的焦点为
的焦点为 ,过点
,过点 的直线
的直线 与抛物线相交于
与抛物线相交于 ,
, 两点,线段
两点,线段 的中点为
的中点为 .过点
.过点 ,
, 分别向
分别向 的准线作垂线,垂足分别为点
的准线作垂线,垂足分别为点 ,
, ,过点
,过点 向
向 的准线作垂线,交抛物线于点
的准线作垂线,交抛物线于点 ,交准线于点
,交准线于点 ,
, 为坐标原点,则( )
为坐标原点,则( )A.以 为直径的圆与直线 为直径的圆与直线 相切 相切 | B. |
C.当 时,点 时,点 , , , , 共线 共线 | D. |
您最近一年使用:0次
3 . 已知抛物线 的焦点为
的焦点为 ,准线交
,准线交 轴于点
轴于点 ,直线
,直线 经过
经过 且与
且与 交于
交于 两点,其中点A在第一象限,线段
两点,其中点A在第一象限,线段 的中点
的中点 在
在 轴上的射影为点
轴上的射影为点 .若
.若 ,则( )
,则( )
 的焦点为
的焦点为 ,准线交
,准线交 轴于点
轴于点 ,直线
,直线 经过
经过 且与
且与 交于
交于 两点,其中点A在第一象限,线段
两点,其中点A在第一象限,线段 的中点
的中点 在
在 轴上的射影为点
轴上的射影为点 .若
.若 ,则( )
,则( )A. 的斜率为 的斜率为 |
B. 是锐角三角形 是锐角三角形 |
C.四边形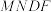 的面积是 的面积是 |
D. |
您最近一年使用:0次
2024-09-04更新
|
1659次组卷
|
6卷引用:第07讲 抛物线及其性质(八大题型)(讲义)-2
名校
解题方法
4 . 已知抛物线 关于
关于 轴对称,焦点在
轴对称,焦点在 正半轴,以焦点和准线上的两点为顶点的三角形是边长为
正半轴,以焦点和准线上的两点为顶点的三角形是边长为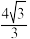 的等边三角形.
的等边三角形.
(1)若直线 绕点
绕点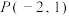 旋转,讨论直线
旋转,讨论直线 与抛物线
与抛物线 的公共点个数;
的公共点个数;
(2)设抛物线 的焦点为
的焦点为 ,从点
,从点 发出的光线经过抛物线上的点
发出的光线经过抛物线上的点 (不同于抛物线的顶点)反射,求证:反射光线平行于抛物线的对称轴.
(不同于抛物线的顶点)反射,求证:反射光线平行于抛物线的对称轴.
 关于
关于 轴对称,焦点在
轴对称,焦点在 正半轴,以焦点和准线上的两点为顶点的三角形是边长为
正半轴,以焦点和准线上的两点为顶点的三角形是边长为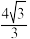 的等边三角形.
的等边三角形.(1)若直线
 绕点
绕点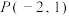 旋转,讨论直线
旋转,讨论直线 与抛物线
与抛物线 的公共点个数;
的公共点个数;(2)设抛物线
 的焦点为
的焦点为 ,从点
,从点 发出的光线经过抛物线上的点
发出的光线经过抛物线上的点 (不同于抛物线的顶点)反射,求证:反射光线平行于抛物线的对称轴.
(不同于抛物线的顶点)反射,求证:反射光线平行于抛物线的对称轴.
您最近一年使用:0次
解题方法
5 . 已知抛物线 的焦点为
的焦点为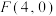 ,则
,则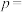
______ ;若斜率为 的直线
的直线 过焦点
过焦点 且与抛物线交于
且与抛物线交于 两点,
两点, 的中垂线交
的中垂线交 轴于点
轴于点 ,则
,则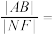
______ .
 的焦点为
的焦点为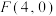 ,则
,则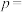
 的直线
的直线 过焦点
过焦点 且与抛物线交于
且与抛物线交于 两点,
两点, 的中垂线交
的中垂线交 轴于点
轴于点 ,则
,则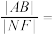
您最近一年使用:0次
6 . 已知抛物线 的焦点为
的焦点为 ,过点
,过点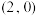 的动直线与
的动直线与 交于M,N两点,则下列说法正确的是( )
交于M,N两点,则下列说法正确的是( )
 的焦点为
的焦点为 ,过点
,过点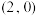 的动直线与
的动直线与 交于M,N两点,则下列说法正确的是( )
交于M,N两点,则下列说法正确的是( )A.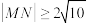 |
B.若 ,则 ,则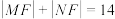 |
C.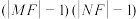 为定值 为定值 |
D.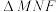 为钝角三角形 为钝角三角形 |
您最近一年使用:0次
7 . 已知 为抛物线
为抛物线 :
: 的焦点,过点
的焦点,过点 且倾斜角为
且倾斜角为 的直线
的直线 与抛物线
与抛物线 相交于不同的两点
相交于不同的两点 ,若抛物线
,若抛物线 在
在 两点处的切线相交于点
两点处的切线相交于点 ,则
,则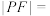
________ .
 为抛物线
为抛物线 :
: 的焦点,过点
的焦点,过点 且倾斜角为
且倾斜角为 的直线
的直线 与抛物线
与抛物线 相交于不同的两点
相交于不同的两点 ,若抛物线
,若抛物线 在
在 两点处的切线相交于点
两点处的切线相交于点 ,则
,则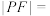
您最近一年使用:0次
8 . 已知椭圆 :
: 的左右焦点分别为
的左右焦点分别为 ,
, ,离心率为
,离心率为 ,过抛物线
,过抛物线 :
: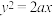 焦点的直线交抛物线于M,N两点,
焦点的直线交抛物线于M,N两点, 的最小值为4.连接
的最小值为4.连接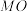 ,
,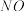 并延长分别交
并延长分别交 于A,B两点,且点A与点M,点B与点N均不在同一象限,
于A,B两点,且点A与点M,点B与点N均不在同一象限, 与
与 的面积分别记为
的面积分别记为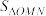 ,
,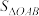 .
.
(1)求 和
和 的方程;
的方程;
(2)记 ,求
,求 的最小值.
的最小值.
 :
: 的左右焦点分别为
的左右焦点分别为 ,
, ,离心率为
,离心率为 ,过抛物线
,过抛物线 :
: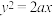 焦点的直线交抛物线于M,N两点,
焦点的直线交抛物线于M,N两点, 的最小值为4.连接
的最小值为4.连接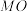 ,
,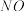 并延长分别交
并延长分别交 于A,B两点,且点A与点M,点B与点N均不在同一象限,
于A,B两点,且点A与点M,点B与点N均不在同一象限, 与
与 的面积分别记为
的面积分别记为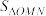 ,
,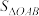 .
.(1)求
 和
和 的方程;
的方程;(2)记
 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
9 . 已知抛物线 的焦点为
的焦点为 ,点
,点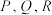 为
为 上可相互重合的点,且
上可相互重合的点,且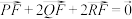 ,则
,则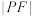 的取值范围是
的取值范围是________ ,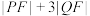 的最小值是
的最小值是________ .
 的焦点为
的焦点为 ,点
,点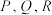 为
为 上可相互重合的点,且
上可相互重合的点,且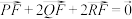 ,则
,则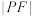 的取值范围是
的取值范围是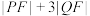 的最小值是
的最小值是
您最近一年使用:0次
2024-06-28更新
|
355次组卷
|
5卷引用:第07讲 抛物线及其性质(八大题型)(讲义)-1
(已下线)第07讲 抛物线及其性质(八大题型)(讲义)-1山西省长治市2023-2024学年高二下学期6月期末数学试题山东省济南市名校教研联盟2023-2024学年高二下学期6月月考数学试卷山西省阳泉市第一中学校2023-2024学年高二下学期期末测试数学试卷(已下线)第54题 抛物线焦点弦性质的应用(高二暑假弯道超车)
2024高三下·全国·专题练习
解题方法
10 . 已知直线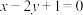 与抛物线
与抛物线 交于
交于 两点,且
两点,且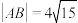 .
.
(1)求 ;
;
(2)设F为C的焦点,M,N为C上两点,且 ,求
,求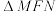 面积的最小值.
面积的最小值.
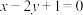 与抛物线
与抛物线 交于
交于 两点,且
两点,且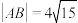 .
.(1)求
 ;
;(2)设F为C的焦点,M,N为C上两点,且
 ,求
,求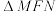 面积的最小值.
面积的最小值.
您最近一年使用:0次



