1 . 在直角坐标系 中,已知抛物线C:
中,已知抛物线C: 的焦点为F,过F的直线l与C交于M,N两点,且当l的斜率为1时,
的焦点为F,过F的直线l与C交于M,N两点,且当l的斜率为1时,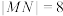 .
.
(1)求C的方程;
(2)设l与C的准线交于点P,直线PO与C交于点Q(异于原点),线段MN的中点为R,若 ,求
,求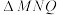 面积的取值范围.
面积的取值范围.
 中,已知抛物线C:
中,已知抛物线C: 的焦点为F,过F的直线l与C交于M,N两点,且当l的斜率为1时,
的焦点为F,过F的直线l与C交于M,N两点,且当l的斜率为1时,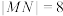 .
.(1)求C的方程;
(2)设l与C的准线交于点P,直线PO与C交于点Q(异于原点),线段MN的中点为R,若
 ,求
,求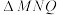 面积的取值范围.
面积的取值范围.
您最近一年使用:0次
2024-04-18更新
|
774次组卷
|
5卷引用:浙江省杭州市源清中学2024-2025学年高三上学期9月考试数学试题
浙江省杭州市源清中学2024-2025学年高三上学期9月考试数学试题福建省福州市2024届高三第三次质量检测数学试题 福建省厦门市2024届高中毕业班第三次质量检测数学试题(已下线)专题9 圆锥曲线中的范围、最值问题【练】(压轴大全)(已下线)重难点突破17 圆锥曲线中参数范围与最值问题(八大题型)
2 . 抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出;反之,平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.如图,已知抛物线 的准线为
的准线为 为坐标原点,在
为坐标原点,在 轴上方有两束平行于
轴上方有两束平行于 轴的入射光线
轴的入射光线 和
和 ,分别经
,分别经 上的点
上的点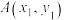 和点
和点 反射后,再经
反射后,再经 上相应的点
上相应的点 和点
和点 反射,最后沿直线
反射,最后沿直线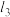 和
和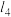 射出,且
射出,且 与
与 之间的距离等于
之间的距离等于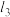 与
与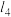 之间的距离.则下列说法中正确的是( )
之间的距离.则下列说法中正确的是( )
 的准线为
的准线为 为坐标原点,在
为坐标原点,在 轴上方有两束平行于
轴上方有两束平行于 轴的入射光线
轴的入射光线 和
和 ,分别经
,分别经 上的点
上的点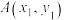 和点
和点 反射后,再经
反射后,再经 上相应的点
上相应的点 和点
和点 反射,最后沿直线
反射,最后沿直线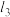 和
和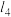 射出,且
射出,且 与
与 之间的距离等于
之间的距离等于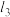 与
与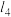 之间的距离.则下列说法中正确的是( )
之间的距离.则下列说法中正确的是( )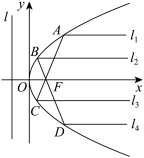
A.若直线 与准线 与准线 相交于点 相交于点 ,则 ,则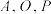 三点共线 三点共线 |
B.若直线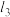 与准线 与准线 相交于点 相交于点 ,则 ,则 平分 平分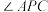 |
C.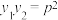 |
D.若直线 的方程为 的方程为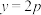 ,则 ,则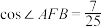 |
您最近一年使用:0次
3 . 已知 为坐标原点,F为抛物线C:
为坐标原点,F为抛物线C: 的焦点,过点
的焦点,过点 的直线
的直线 交C于A、B两点,直线
交C于A、B两点,直线 、
、 分别交C于M、N,则
分别交C于M、N,则 的最小值为
的最小值为___________
 为坐标原点,F为抛物线C:
为坐标原点,F为抛物线C: 的焦点,过点
的焦点,过点 的直线
的直线 交C于A、B两点,直线
交C于A、B两点,直线 、
、 分别交C于M、N,则
分别交C于M、N,则 的最小值为
的最小值为
您最近一年使用:0次
4 . 已知O为坐标原点,F为抛物线 :
: 的焦点,过点F且倾斜角为
的焦点,过点F且倾斜角为 的直线
的直线 交C于A、B两点(其中点A在第一象限),过线段
交C于A、B两点(其中点A在第一象限),过线段 的中点P作垂直于抛物线准线的直线,与准线交于点N,则下列说法正确的是( )
的中点P作垂直于抛物线准线的直线,与准线交于点N,则下列说法正确的是( )
 :
: 的焦点,过点F且倾斜角为
的焦点,过点F且倾斜角为 的直线
的直线 交C于A、B两点(其中点A在第一象限),过线段
交C于A、B两点(其中点A在第一象限),过线段 的中点P作垂直于抛物线准线的直线,与准线交于点N,则下列说法正确的是( )
的中点P作垂直于抛物线准线的直线,与准线交于点N,则下列说法正确的是( )A.C的准线方程为 | B.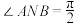 |
C.三角形 的面积 的面积 | D.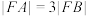 |
您最近一年使用:0次
名校
解题方法
5 . 已知 为拋物线
为拋物线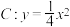 的焦点,过点
的焦点,过点 的直线
的直线 与拋物线
与拋物线 交于不同的两点
交于不同的两点 ,
, ,拋物线在点
,拋物线在点 处的切线分别为
处的切线分别为 和
和 ,若
,若 和
和 交于点
交于点 ,则
,则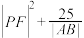 的最小值为
的最小值为__________ .
 为拋物线
为拋物线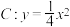 的焦点,过点
的焦点,过点 的直线
的直线 与拋物线
与拋物线 交于不同的两点
交于不同的两点 ,
, ,拋物线在点
,拋物线在点 处的切线分别为
处的切线分别为 和
和 ,若
,若 和
和 交于点
交于点 ,则
,则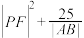 的最小值为
的最小值为
您最近一年使用:0次
2024-01-18更新
|
2242次组卷
|
5卷引用:浙江省湖州市第一中学2024届高三下学期新高考数学模拟试题
浙江省湖州市第一中学2024届高三下学期新高考数学模拟试题辽宁省葫芦岛市2024届高三上学期1月学业质量监测考试数学试题山东省济南市山东实验中学2024届高三上学期第一次模拟测试数学试题(已下线)(新高考新结构)2024年高考数学模拟卷(三)(已下线)专题07 直线与圆、圆锥曲线
名校
解题方法
6 . 已知 是抛物线
是抛物线 的焦点,直线
的焦点,直线 经过点
经过点 交抛物线于A、B两点,则下列说法正确的是( )
交抛物线于A、B两点,则下列说法正确的是( )
 是抛物线
是抛物线 的焦点,直线
的焦点,直线 经过点
经过点 交抛物线于A、B两点,则下列说法正确的是( )
交抛物线于A、B两点,则下列说法正确的是( )A.以 为直径的圆与抛物线的准线相切 为直径的圆与抛物线的准线相切 |
B.若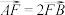 ,则直线 ,则直线 的斜率 的斜率 |
C.弦 的中点 的中点 的轨迹为一条抛物线,其方程为 的轨迹为一条抛物线,其方程为 |
D.若 ,则 ,则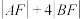 的最小值为18 的最小值为18 |
您最近一年使用:0次
2024-01-10更新
|
801次组卷
|
7卷引用:浙江省湖州市湖州中学2024届高三上学期第一次质量检测数学试题
浙江省湖州市湖州中学2024届高三上学期第一次质量检测数学试题河南省南阳市2023-2024学年高二上学期期中数学试题湖南省长沙市长郡中学2023-2024学年高二上学期阶段性检测数学试卷(已下线)模块五 专题6 期末全真模拟(拔高卷2)期末终极研习室(高二人教A版)河北省保定市唐县第一中学2023-2024学年高二上学期阶段性检测数学试题(已下线)3.3.2 抛物线的简单的几何性质(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)【课后练】 3.3.2 抛物线的简单几何性质 课后作业-湘教版(2019)选择性必修第一册 第3章 圆锥曲线与方程
名校
解题方法
7 . 设 为抛物线
为抛物线 :
: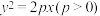 的焦点,过点
的焦点,过点 的直线
的直线 与抛物线
与抛物线 交于
交于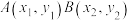 两点,过
两点,过 作与
作与 轴平行的直线,和过点
轴平行的直线,和过点 且与
且与 垂直的直线交于点
垂直的直线交于点 ,
, 与
与 轴交于点
轴交于点 ,则( )
,则( )
 为抛物线
为抛物线 :
: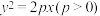 的焦点,过点
的焦点,过点 的直线
的直线 与抛物线
与抛物线 交于
交于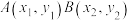 两点,过
两点,过 作与
作与 轴平行的直线,和过点
轴平行的直线,和过点 且与
且与 垂直的直线交于点
垂直的直线交于点 ,
, 与
与 轴交于点
轴交于点 ,则( )
,则( )A.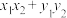 为定值 为定值 |
B.当直线 的斜率为 的斜率为 时, 时, 的面积为 的面积为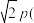 其中 其中 为坐标原点 为坐标原点 |
C.若 为 为 的准线上任意一点,则直线 的准线上任意一点,则直线 , ,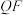 , ,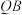 的斜率成等差数列 的斜率成等差数列 |
D.点 到直线 到直线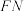 的距离为 的距离为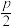 |
您最近一年使用:0次
2023-04-09更新
|
1535次组卷
|
3卷引用:浙江省杭州地区(含周边重点中学)2023届高三一模数学试题
浙江省杭州地区(含周边重点中学)2023届高三一模数学试题(已下线)第五篇 向量与几何 专题11 圆锥曲线中的蝴蝶定理 微点3 圆锥曲线中的蝴蝶定理综合训练江苏省无锡市第一中学2023-2024学年高二上学期12月质量检测数学试卷
解题方法
8 . 已知抛物线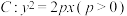 ,过焦点
,过焦点 的直线交抛物线
的直线交抛物线 于
于 ,
, 两点,且
两点,且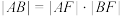 .
.
(1)求抛物线 的方程;
的方程;
(2)若点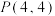 ,直线
,直线 ,
, 分别交准线
分别交准线 于
于 ,
, 两点,证明:以线段
两点,证明:以线段 为直径的圆过定点.
为直径的圆过定点.
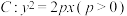 ,过焦点
,过焦点 的直线交抛物线
的直线交抛物线 于
于 ,
, 两点,且
两点,且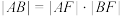 .
.(1)求抛物线
 的方程;
的方程;(2)若点
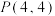 ,直线
,直线 ,
, 分别交准线
分别交准线 于
于 ,
, 两点,证明:以线段
两点,证明:以线段 为直径的圆过定点.
为直径的圆过定点.
您最近一年使用:0次
解题方法
9 . 已知抛物线 的焦点为
的焦点为 ,过点
,过点 作直线
作直线 交抛物线于点
交抛物线于点 ,过
,过 分别向抛物线
分别向抛物线 的准线作垂线,垂足分别为
的准线作垂线,垂足分别为 ,线段
,线段 的中点为
的中点为 ,则( )
,则( )
 的焦点为
的焦点为 ,过点
,过点 作直线
作直线 交抛物线于点
交抛物线于点 ,过
,过 分别向抛物线
分别向抛物线 的准线作垂线,垂足分别为
的准线作垂线,垂足分别为 ,线段
,线段 的中点为
的中点为 ,则( )
,则( )A. | B. |
C.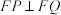 | D.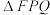 面积的最小值为4 面积的最小值为4 |
您最近一年使用:0次
10 . 抛物线 ,过焦点
,过焦点 的直线
的直线 与抛物线
与抛物线 交于
交于 两点(点A在第一象限),
两点(点A在第一象限),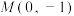 ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,过焦点
,过焦点 的直线
的直线 与抛物线
与抛物线 交于
交于 两点(点A在第一象限),
两点(点A在第一象限),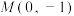 ,则下列说法正确的是( )
,则下列说法正确的是( )A. 最小值为4 最小值为4 |
B.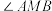 有可能是钝角 有可能是钝角 |
C.当直线 的倾斜角为 的倾斜角为 时, 时,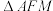 与 与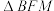 面积之比为3 面积之比为3 |
D.当直线 与抛物线 与抛物线 只有一个公共点时, 只有一个公共点时,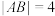 |
您最近一年使用:0次



