1 . 已知椭圆C的方程为 ,右焦点为
,右焦点为 ,且离心率为
,且离心率为 .
.
(1)求椭圆C的方程;
(2)设M,N是椭圆C上的两点,直线 与曲线
与曲线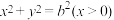 相切.证明:M,N,F三点共线的充要条件是
相切.证明:M,N,F三点共线的充要条件是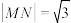 .
.
 ,右焦点为
,右焦点为 ,且离心率为
,且离心率为 .
.(1)求椭圆C的方程;
(2)设M,N是椭圆C上的两点,直线
 与曲线
与曲线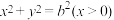 相切.证明:M,N,F三点共线的充要条件是
相切.证明:M,N,F三点共线的充要条件是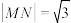 .
.
您最近一年使用:0次
2021-06-25更新
|
54145次组卷
|
81卷引用:安徽省滁州市滁州中学2023-2024学年高二上学期期末数学试题
安徽省滁州市滁州中学2023-2024学年高二上学期期末数学试题(已下线)第2章《圆锥曲线与方程》章节复习巩固(提高练)-2021-2022学年高二数学同步训练精选新题汇编(人教A版选修2-1)辽宁省铁岭市清河高级中学2021-2022学年高二上学期第一次阶段考试数学试题(已下线)专题29 《圆锥曲线与方程》中的高考真题训练-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册) 湖北省武汉市第二十三中学2021-2022学年高二上学期12月月考数学试题(已下线)第15讲 椭圆-【暑假自学课】2022年新高二数学暑假精品课(人教版2019必修第二册+选择性必修第一册)湘教版(2019) 选修第一册 突围者 第3章 章末培优专练2023版 北师大版(2019) 选修第一册 突围者 第二章 章末培优专练2023版 苏教版(2019) 选修第一册 突围者 第3章 章末培优专练2023版 湘教版(2019) 选修第一册 过关斩将 第3章 综合拔高练河南省南阳市宛城区第五中学校2022-2023学年高二上学期12月月考数学试题湖北省武汉市华中师范大学第一附属中学2022-2023学年高二上学期12 月月考数学试题(已下线)综合检测(基础篇)-2022-2023学年高二数学同步知识梳理+考点精讲精练(人教B版2019选择性必修第一册)3.1 椭圆黑龙江省牡丹江市第二高级中学2023-2024学年高二上学期期中数学试题湖南省张家界市慈利县第一中学2022-2023学年高二上学期第四次月考数学试题专题08椭圆问题(解答题)2021年全国新高考II卷数学试题(已下线)考点38 直线与圆锥曲线的位置关系-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点34 直线与圆锥曲线-备战2022年高考数学(理)一轮复习考点微专题广东省广州市执信中学2022届高三上学期9月月考数学试题(已下线)考点43 直线与圆锥曲线的位置关系-备战2022年高考数学(理)一轮复习考点帮(已下线)考点40 椭圆-备战2022年高考数学(理)一轮复习考点帮(已下线)考点38 椭圆-备战2022年高考数学(文)一轮复习考点帮(已下线)考点41 直线与圆锥曲线的位置关系-备战2022年高考数学(文)一轮复习考点帮(已下线)专题05 平面解析几何-2021年高考真题和模拟题数学(文)分项汇编(全国通用)(已下线)专题05 平面解析几何-五年(2017-2021)高考数学真题分项汇编(文科+理科)上海市2022届高三上学期仿真预测押题数学试题(已下线)专题02 圆锥曲线弦长问题-【解题思路培养】2022年高考数学一轮复习解答题拿分秘籍(全国通用版)(已下线)专题28 椭圆-2022年高三毕业班数学常考点归纳与变式演练(理科专用)(已下线)专题9.7 圆锥曲线综合问题 2022年高考数学一轮复习讲练测(新教材新高考)(讲)(已下线)考向40 椭圆(已下线)2021年全国新高考II卷数学试题变式题18-22题(已下线)专题31 直线与圆锥曲线的位置关系-2022年高三毕业班数学常考点归纳与变式演练(文理通用)(已下线)专题03 平面解析几何-备战2022年高考数学母题题源解密(新高考版)(已下线)第2讲 圆锥曲线的定义、方程与性质(练)-2022年高考数学二轮复习讲练测(新教材·新高考地区专用)(已下线)专题13解析几何中的定值、定点和定线问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》北京市一零一中学2022届高三下学期入学考试数学试卷题(已下线)专题26 圆锥曲线(理科)解答题20题-备战2022年高考数学冲刺横向强化精练精讲(已下线)热点12 圆锥曲线中综合问题-2022年高考数学【热点·重点·难点】专练(全国通用)(已下线)专题25 真题优选重组第二卷-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)(已下线)专题22圆锥曲线解答题20题-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)(已下线)押新高考第21题 圆锥曲线-备战2022年高考数学临考题号押题(新高考专用)(已下线)回归教材重难点04 圆锥曲线-【查漏补缺】2022年高考数学(文)三轮冲刺过关(已下线)回归教材重难点04 圆锥曲线-【查漏补缺】2022年高考数学(理)三轮冲刺过关(已下线)查补易混易错点06 解析几何-【查漏补缺】2022年高考数学三轮冲刺过关(新高考专用)(已下线)2022年高考考前20天终极冲刺攻略(三)【理科数学】 (5月30日)(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(5月29日)(已下线)2022年高考考前最后一课-数学(正式版)-考前技能篇(已下线)第7讲 解析几何(已下线)专题6 圆锥曲线硬解定理 微点1 圆锥曲线硬解定理(已下线)数学-2022年高考押题预测卷03(北京卷)(已下线)专题55:椭圆-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题19 圆锥曲线解答题(已下线)专题17 解析几何解答题(已下线)专题13 极坐标秒解圆锥曲线 微点1 极坐标秒解圆锥曲线(已下线)第13讲 椭圆-2(已下线)11.4 直线与圆锥曲线的位置关系(已下线)专题13 圆锥曲线压轴解答题常考套路归类(精讲精练)-2江苏省扬州市新华中学2022-2023学年高三下学期开学检测数学试题四川省内江市威远中学校2022-2023学年高三下学期第一次月考数学(理)试题四川省内江市威远中学校2022-2023学年高三下学期第一次月考数学(文)试题(已下线)押新高考第21题 圆锥曲线专题07平面解析几何(成品)专题07平面解析几何(添加试题分类成品)陕西省安康市石泉县江南中学2023届高三下学期2月月考数学(文)试题陕西省安康市石泉县江南中学2023届高三下学期2月月考理科数学试题(已下线)考点14 直线与圆锥曲线相交问题 2024届高考数学考点总动员(已下线)专题15 圆锥曲线综合(已下线)专题06 直线与圆、椭圆方程(分层练)(三大题型+12道精选真题)(已下线)第5讲:定点、定值、定直线问题【练】(已下线)专题01 集合与常用逻辑用语-2(已下线)第十章 圆锥曲线10.1 椭圆(已下线)7.2 椭圆(高考真题素材之十年高考)(已下线)专题24 解析几何解答题(文科)-1(已下线)专题04 高考解几大题真题精练(已下线)专题24 解析几何解答题(理科)-3(已下线)五年新高考专题10平面解析几何(已下线)专题7 圆锥曲线硬解定理【讲】(已下线)专题31 设而不求点差法,整体思想是主线(一题多变)(已下线)第08讲 直线与圆锥曲线的位置关系(八大题型)(练习)-2
2 .
已知点A(−2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率之积为− .记M的轨迹为曲线C.
.记M的轨迹为曲线C.
(1)求C的方程,并说明C是什么曲线;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.
(i)证明: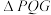 是直角三角形;
是直角三角形;
(ii)求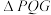 面积的最大值.
面积的最大值.
您最近一年使用:0次
2019-06-09更新
|
36662次组卷
|
63卷引用:山西省晋城市高平一中、阳城一中、高平实验中学2020-2021学年高二上学期期末联考数学(理)试题
山西省晋城市高平一中、阳城一中、高平实验中学2020-2021学年高二上学期期末联考数学(理)试题山西省晋城市(高平一中、阳城一中、高平实验中学)2020-2021学年高二上学期期末数学(理)试题湖南省常德市临澧县第一中学2022-2023学年高二上学期期末数学试题黑龙江省哈尔滨市尚志市尚志中学2019-2020学年高二上学期第三次月考数学(理)试卷黑龙江省哈尔滨市尚志市尚志中学2019-2020学年高二上学期第三次月考数学(文)试卷人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.8 综合拔高练人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 3.1 综合拔高练黑龙江省双鸭山一中2020-2021学年高二(10月分)第一次月考数学(理科)试题安徽省淮北市第一中学2020-2021学年高二上学期期中数学试题苏教版(2019) 选修第一册 突围者 第3章 章末培优专练人教B版(2019) 选修第一册 过关检测 第二章 专项把关练2023版 湘教版(2019) 选修第一册 过关斩将 第3章 综合拔高练沪教版(2020) 选修第一册 精准辅导 第2章 2.5(1) 求轨迹方程3.1 椭圆2019年全国统一高考数学试卷(理科)(新课标Ⅱ)(已下线)专题05 平面解析几何——2019年高考真题和模拟题理科数学分项汇编(已下线)专题9.8 直线与圆锥曲线的位置关系(讲)-浙江版《2020年高考一轮复习讲练测》上海市交通大学附属中学2019-2020学年高三上学期9月月考数学试题(已下线)专题02 化繁为简,轻松驾驭解析几何运算有技巧(第五篇)-2020高考数学压轴题命题区间探究与突破(已下线)专题19 圆锥曲线综合-2020年高考数学(理)母题题源解密(全国Ⅱ专版)(已下线)易错点09 解析几何-备战2021年新高考数学一轮复习易错题(已下线)专题08 平面解析几何(解答题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题29 圆锥曲线的综合问题-十年(2011-2020)高考真题数学分项(已下线)专题15 直线与椭圆、抛物线的位置关系-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】(已下线)专题9.9 高考解答题热点题型(一)圆锥曲线中的范围、最值问题-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破(已下线)考点42 曲线与方程-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题9.7 圆锥曲线综合问题(精讲)-2021年新高考数学一轮复习学与练(已下线)专题9.7 圆锥曲线综合问题(练)-2021年新高考数学一轮复习讲练测(已下线)考点35 椭圆的标准方程及几何性质-备战2021年新高考数学一轮复习考点一遍过(已下线)专题13 解析几何中的范围、最值和探索性问题 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)专题17 圆锥曲线中的椭圆问题-2021年高考数学二轮优化提升专题训练(新高考地区专用)【学科网名师堂】(已下线)专题4.5 圆锥曲线-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)数学-2021年高考考前20天终极冲刺攻略(三)(新高考地区专用)【学科网名师堂】 (5月30日)(已下线)押第20题 解析几何-备战2021年高考数学(理)临考题号押题(全国卷1)(已下线)解密18 椭圆(分层训练)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练(已下线)预测10 圆锥曲线中的综合性问题-【临门一脚】2021年高考数学三轮冲刺过关(新高考专用)【学科网名师堂】(已下线)押第20题 圆锥曲线-备战2021年高考数学(理)临考题号押题(全国卷2)(已下线)专题9.7 圆锥曲线综合问题 2022年高考数学一轮复习讲练测(新教材新高考)(讲)(已下线)专题9.7 圆锥曲线综合问题 2022年高考数学一轮复习讲练测(新教材新高考)(练)(已下线)专题20 椭圆、抛物线(解答题)-备战2022年高考数学(理)母题题源解密(全国甲卷)(已下线)专题13圆锥曲线范围最值问题(练)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题13圆锥曲线范围最值问题(讲)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题40 轨迹方程求解方法-学会解题之高三数学万能解题模板【2022版】(已下线)技巧04 解答题解法与技巧(讲)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题42 盘点圆锥曲线中的面积问题——备战2022年高考数学二轮复习常考点专题突破(已下线)专题4 圆锥曲线的综合应用-学会解题之高三数学321训练体系【2022版】(已下线)押全国卷(理科)第20题 圆锥曲线-备战2022年高考数学(理)临考题号押题(全国卷)(已下线)专题19 圆锥曲线解答题(已下线)考点23圆锥曲线综合应用-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)(已下线)专题23 圆锥曲线中的最值、范围问题 微点1 圆锥曲线中的最值问题(已下线)考向37 圆锥曲线中的范围、最值问题(重点)上海市浦东复旦附中分校2022届高三上学期10月月考数学试题上海市2023届高三二模暨秋考模拟7数学试题全国甲乙卷真题5年分类汇编《解析几何》解答题黑龙江省大庆市肇州县第二中学2023届高三下学期开学考试数学试题广东省深圳市红岭中学2023-2024学年高三第五次统一考试数学试题河南省信阳市浉河区信阳高级中学2024届高三上学期1月月考数学试题(已下线)专题2 垂径定理 拓展延伸 练(已下线)7.5 直线和圆锥曲线的综合问题(高考真题素材之十年高考)(已下线)专题24 解析几何解答题(理科)-3专题36平面解析几何解答题(第一部分)(已下线)专题15 利用仿射变换解椭圆、双曲线综合题(一)(高三压轴题)【讲】(已下线)专题15 利用仿射变换解椭圆、双曲线综合题(二)(高三压轴题)【讲】
名校
解题方法
3 . 已知椭圆 的离心率为
的离心率为 ,焦距为
,焦距为 ,过
,过 的左焦点
的左焦点 的直线
的直线 与
与 相交于
相交于 、
、 两点,与直线
两点,与直线 相交于点
相交于点 .
.
(1)若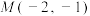 ,求证:
,求证: ;
;
(2)过点 作直线
作直线 的垂线
的垂线 与
与 相交于
相交于 、
、 两点,与直线
两点,与直线 相交于点
相交于点 .求
.求 的最大值.
的最大值.
 的离心率为
的离心率为 ,焦距为
,焦距为 ,过
,过 的左焦点
的左焦点 的直线
的直线 与
与 相交于
相交于 、
、 两点,与直线
两点,与直线 相交于点
相交于点 .
.(1)若
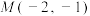 ,求证:
,求证: ;
;(2)过点
 作直线
作直线 的垂线
的垂线 与
与 相交于
相交于 、
、 两点,与直线
两点,与直线 相交于点
相交于点 .求
.求 的最大值.
的最大值.
您最近一年使用:0次
2023-03-29更新
|
3583次组卷
|
14卷引用:江苏省南京市2023-2024学年高二上学期期末模拟数学试题
江苏省南京市2023-2024学年高二上学期期末模拟数学试题江苏省淮安市淮阴中学2023-2024学年高二上学期10月阶段练习数学试题河北省石家庄正定中学2023-2024学年高二上学期期中数学试题专题08椭圆问题(解答题)江苏省八市(南通、泰州、扬州、徐州、淮安、连云港、宿迁、盐城)2023届高三二模数学试题(已下线)专题14圆锥曲线中的最值、范围、探索问题(已下线)江苏省八市2023届高三二模数学试题变式题17-22专题20平面解析几何(解答题)(已下线)重难点突破17 圆锥曲线中参数范围与最值问题(八大题型)(已下线)重难点突破06 弦长问题及长度和、差、商、积问题(七大题型)-2江苏省八市2023届高三下学期第二次调研测试数学试题四川省成都市石室中学2023-2024学年高一下学期开学考试数学(理科)试卷四川省成都市石室中学2023-2024学年高一下学期开学考试数学(文科)试卷四川省成都第十二中学2023届高三下学期三诊模拟考试文科数学试卷
名校
解题方法
4 . 椭圆C的中心在坐标原点O,焦点在x轴上,椭圆C经过点 且长轴长为
且长轴长为 .
.
(1)求椭圆C的标准方程;
(2)过点 且斜率为1的直线l与椭圆C交于A,B两点,求弦长|AB|.
且斜率为1的直线l与椭圆C交于A,B两点,求弦长|AB|.
 且长轴长为
且长轴长为 .
.(1)求椭圆C的标准方程;
(2)过点
 且斜率为1的直线l与椭圆C交于A,B两点,求弦长|AB|.
且斜率为1的直线l与椭圆C交于A,B两点,求弦长|AB|.
您最近一年使用:0次
2023-03-26更新
|
2342次组卷
|
19卷引用:新疆泽普县第二中学2022-2023学年高二上学期期末考试数学试题
新疆泽普县第二中学2022-2023学年高二上学期期末考试数学试题云南巍山彝族回族自治县第二中学2021-2022学年高二下学期第四次月考数学试题广东省深圳市南头中学2022-2023学年高二上学期期中数学试题河南省濮阳市油田第二高级中学2022-2023学年高二10月月考数学试题(已下线)3.1.2 椭圆的几何性质(2)(已下线)第24讲 圆锥曲线弦长面积问题海南省东方市东方中学2022-2023学年高二下学期期中考试数学试题(已下线)模块三 专题10 椭圆 A基础卷甘肃省武威市天祝藏族自治县第一中学2022-2023学年高二下学期开学考试数学试题(已下线)模块三 专题13 椭圆 A基础卷江西省九江市庐山市匡庐星瀚高级中学2023-2024学年高二上学期期中数学试题(已下线)第04讲 拓展一:直线与椭圆的位置关系-【练透核心考点】2023-2024学年高二数学上学期重点题型方法与技巧(人教A版2019选择性必修第一册)广东惠州市泰雅实验高中2023-2024学年高二上学期第二次月考数学试题单元测试A卷——第三章 圆锥曲线的方程(已下线)9.2 椭圆(精练)(提升版)-2(已下线)10.3 椭圆(精讲)新疆生产建设兵团第二师八一中学2023届高三上学期第一次月考数学(文)试题海南省海口嘉勋高级中学2023届高三上学期11月期中检测数学试题(已下线)考点14 直线与圆锥曲线相交问题 2024届高考数学考点总动员【练】
5 . 已知椭圆的中心在原点,焦点在 轴上,离心率为
轴上,离心率为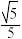 ,焦距为2.
,焦距为2.
(1)求椭圆的标准方程;
(2)过椭圆的左焦点 ,且斜率为
,且斜率为 的直线
的直线 交椭圆于A,
交椭圆于A, 两点,求
两点,求 的面积.
的面积.
 轴上,离心率为
轴上,离心率为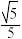 ,焦距为2.
,焦距为2.(1)求椭圆的标准方程;
(2)过椭圆的左焦点
 ,且斜率为
,且斜率为 的直线
的直线 交椭圆于A,
交椭圆于A, 两点,求
两点,求 的面积.
的面积.
您最近一年使用:0次
2023-12-01更新
|
2269次组卷
|
5卷引用:黑龙江省哈尔滨市第四中学校2023-2024学年高二上学期期末数学试题
6 . 已知椭圆 的离心率为
的离心率为 ,焦距为
,焦距为 .斜率为
.斜率为 的直线
的直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 、
、 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若 ,求
,求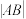 的最大值;
的最大值;
(Ⅲ)设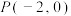 ,直线
,直线 与椭圆
与椭圆 的另一个交点为
的另一个交点为 ,直线
,直线 与椭圆
与椭圆 的另一个交点为
的另一个交点为 .若
.若 、
、 和点
和点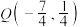 共线,求
共线,求 .
.
 的离心率为
的离心率为 ,焦距为
,焦距为 .斜率为
.斜率为 的直线
的直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 、
、 .
.(Ⅰ)求椭圆
 的方程;
的方程; (Ⅱ)若
 ,求
,求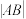 的最大值;
的最大值;(Ⅲ)设
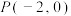 ,直线
,直线 与椭圆
与椭圆 的另一个交点为
的另一个交点为 ,直线
,直线 与椭圆
与椭圆 的另一个交点为
的另一个交点为 .若
.若 、
、 和点
和点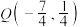 共线,求
共线,求 .
.
您最近一年使用:0次
2018-06-09更新
|
15501次组卷
|
34卷引用:【全国百强校】山西省祁县中学2018-2019学年高二上学期期末模拟一考试数学(理)试题
【全国百强校】山西省祁县中学2018-2019学年高二上学期期末模拟一考试数学(理)试题北京市昌平区新学道临川学校2020-2021学年高二上学期期末考试数学(文)试题天津市和平区2021-2022 学年高二上学期期末质量调查数学试题【校级联考】江西省南昌市第八中学、第二十三中学、第十三中学2018-2019学年高二第一学期期中联考数学(文科)试题新疆奎屯市第一高级中学2018-2019学年高二下学期第一次月考数学(文)试题山东省济南市历城区历城第二中学2019-2020学年高二上学期期中数学试题陕西省西安市西北大学附中2019-2020学年高二上学期期中数学试题(已下线)上海市华东师范大学第二附属中学2020-2021学年高二上学期12月月考数学试题广东省湛江市第二十中学2020-2021学年高二下学期第一阶段考试数学试题重庆市永川北山中学校2022-2023学年高二下学期入学考试数学试题北京市第十二中学2023-2024学年高二上学期12月月考数学试题2018年全国普通高等学校招生统一考试文科数学(北京卷)(已下线)2018年高考题及模拟题汇编 【文科】6.解析几何【全国百强校】江苏省海安高级中学2019届高三12月月考数学试题(已下线)专题9.5 椭圆(讲)-浙江版《2020年高考一轮复习讲练测》(已下线)专题9.8 直线与圆锥曲线位置关系(练)-江苏版《2020年高考一轮复习讲练测》(已下线)专题9.5 椭圆(练)-江苏版《2020年高考一轮复习讲练测》2020届北京东城区五中高三开学考试理科数学试题(已下线)冲刺卷06-决战2020年高考数学冲刺卷(山东专版)(已下线)提升套餐练06-【新题型】2020年新高考数学多选题与热点解答题组合练(已下线)专题08 平面解析几何(解答题)——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题18 解析几何综合-五年(2016-2020)高考数学(文)真题分项(已下线)专题29 圆锥曲线的综合问题-十年(2011-2020)高考真题数学分项(已下线)专题9.6 直线与圆锥曲线(讲)-2021年新高考数学一轮复习讲练测(已下线)专题4.5 圆锥曲线-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)专题11 圆锥曲线-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)押全国卷(文科)第20题 圆锥曲线-备战2022年高考数学(文)临考题号押题(全国卷)(已下线)专题12 定比点差法及其应用 微点1 定比点差法及其应用初步(已下线)重组卷05(已下线)北京十年真题专题08平面解析几何北京十年真题专题08平面解析几何(已下线)专题24 解析几何解答题(文科)-1专题12平面解析几何(第二部分)(已下线)专题3 曲线系方程及其应用【练】(压轴题大全)
名校
解题方法
7 . 已知椭圆 的离心率为
的离心率为 ,焦距为
,焦距为 ,斜率为
,斜率为 的直线
的直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 ,
, .
.
(1)求椭圆 的方程;
的方程;
(2)若 ,求
,求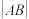 的最大值.
的最大值.
 的离心率为
的离心率为 ,焦距为
,焦距为 ,斜率为
,斜率为 的直线
的直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 ,
, .
.(1)求椭圆
 的方程;
的方程;(2)若
 ,求
,求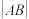 的最大值.
的最大值.
您最近一年使用:0次
2023-09-05更新
|
2073次组卷
|
18卷引用:【全国百强校】内蒙古集宁一中2018-2019学年高二上学期期末考试数学(理)试题
【全国百强校】内蒙古集宁一中2018-2019学年高二上学期期末考试数学(理)试题陕西省咸阳市2019-2020学年高二下学期期末数学(文)试题陕西省榆林市2020-2021学年高二上学期期末文科数学试题西藏拉萨市那曲第二高级中学2020-2021学年高二上学期期末考试数学(理)试题陕西省洛南中学2022-2023学年高二上学期期末数学(文)试题(已下线)模块三 专题6 大题分类练(圆锥曲线)基础夯实练 期末终极研习室(高二人教A版)新疆巴音郭楞蒙古自治州普通高中2023-2024学年高二上学期1月期末考试数学试题(已下线)检测(四)-【专题突破】2021-2022学年高二数学之圆锥曲线与方程(人教A版选修1-1)陕西省洛南中学2022-2023学年高二上学期12月月考数学(文)试题江西省上饶市第一中学2022-2023学年高二上学期期中数学试题(已下线)2.4.2直线与圆锥曲线的综合问题(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)福建省三明第一中学2023-2024学年高二上学期10月月考数学试题(已下线)模块四 专题6 大题分类练(圆锥曲线的方程)基础夯实练(人教A)(已下线)第04讲 拓展一:直线与椭圆的位置关系-【练透核心考点】2023-2024学年高二数学上学期重点题型方法与技巧(人教A版2019选择性必修第一册)(已下线)第3章 圆锥曲线与方程单元检测(基础卷)-2023-2024学年高二数学《重难点题型·高分突破》(苏教版2019选择性必修第一册)内蒙古海拉尔第二中学2021-2022学年高三上学期第三次阶段考数学(理)试题内蒙古海拉尔第二中学2021-2022学年高三上学期第三次阶段考数学(文)试题(已下线)考点巩固卷20 椭圆方程及其性质(十大考点)
名校
解题方法
8 . 经过椭圆 的左焦点
的左焦点 作倾斜角为45°的直线
作倾斜角为45°的直线 ,直线
,直线 与椭圆相交于
与椭圆相交于 两点,
两点, 是椭圆的右焦点.
是椭圆的右焦点.
(1)求 的周长.
的周长.
(2)求 的长.
的长.
 的左焦点
的左焦点 作倾斜角为45°的直线
作倾斜角为45°的直线 ,直线
,直线 与椭圆相交于
与椭圆相交于 两点,
两点, 是椭圆的右焦点.
是椭圆的右焦点.(1)求
 的周长.
的周长.(2)求
 的长.
的长.
您最近一年使用:0次
2023-09-30更新
|
1781次组卷
|
9卷引用:四川省凉山州宁南中学2023-2024学年高二上学期期末模拟数学试题(一)
四川省凉山州宁南中学2023-2024学年高二上学期期末模拟数学试题(一)宁夏银川市永宁县第二中学2022-2023学年高二上学期期中考试数学试题(已下线)模块一 专题3 圆锥曲线的方程(人教A)(2)(已下线)模块四 专题6 大题分类练(圆锥曲线的方程)拔高能力练(人教A)湖北省武汉市汉阳区武汉情智学校2023-2024学年高二上学期11月期中考试数学试题安徽省安庆市桐城市桐城中学2023-2024学年高二上学期第二次教学质量检测数学试题内蒙古自治区优质高中联考2023-2024学年高二上学期11月期中数学试题(已下线)3.1.2 椭圆的简单几何性质(10大题型)精练-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)(已下线)专题3.1 椭圆(5个考点十四大题型)(4)
名校
解题方法
9 . 椭圆C: 左右焦点为
左右焦点为 ,
, ,离心率为
,离心率为 ,点
,点 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)经过点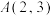 ,倾斜角为
,倾斜角为 直线l与椭圆交于B,C两点,求
直线l与椭圆交于B,C两点,求 .
.
 左右焦点为
左右焦点为 ,
, ,离心率为
,离心率为 ,点
,点 在椭圆C上.
在椭圆C上.(1)求椭圆C的标准方程;
(2)经过点
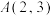 ,倾斜角为
,倾斜角为 直线l与椭圆交于B,C两点,求
直线l与椭圆交于B,C两点,求 .
.
您最近一年使用:0次
2022-07-15更新
|
3526次组卷
|
9卷引用:贵州省遵义市2021-2022学年高二下学期期末质量监测数学(理)试题
贵州省遵义市2021-2022学年高二下学期期末质量监测数学(理)试题贵州省遵义市2021-2022学年高二下学期期末质量监测数学(文)试题(已下线)期中测试卷(基础篇)(范围:第一章+第二章椭圆)-2022-2023学年高二数学上学期同步知识梳理+考点精讲精练(人教B版2019选择性必修第一册)安徽省淮南市第二中学2022-2023学年高二上学期10月月考数学试题(已下线)第24讲 圆锥曲线弦长面积问题云南省昆明市昆明师范专科学校附属中学2023-2024学年高二下学期5月期中学业质量监测数学试题(已下线)第08讲 直线与椭圆、双曲线、抛物线 (精讲)-2(已下线)专题2 求距离运算(基础版)(已下线)专题38 椭圆及其性质-6
10 . 著名古希腊数学家阿基米德首次用“逼近法”的思想得到了椭圆的面积公式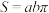 ,(
,( 分别为椭圆的长半轴长和短半轴长)为后续微积分的开拓奠定了基础,已知椭圆
分别为椭圆的长半轴长和短半轴长)为后续微积分的开拓奠定了基础,已知椭圆 :
: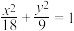 .
.
(1)求 的面积;
的面积;
(2)若直线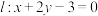 交
交 于
于 两点,求
两点,求 .
.
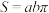 ,(
,( 分别为椭圆的长半轴长和短半轴长)为后续微积分的开拓奠定了基础,已知椭圆
分别为椭圆的长半轴长和短半轴长)为后续微积分的开拓奠定了基础,已知椭圆 :
: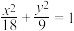 .
.(1)求
 的面积;
的面积;(2)若直线
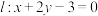 交
交 于
于 两点,求
两点,求 .
.
您最近一年使用:0次
2023-12-31更新
|
1704次组卷
|
5卷引用:上海市华东师范大学第二附属中学2023-2024学年高二上学期数学期末考试试卷
(已下线)上海市华东师范大学第二附属中学2023-2024学年高二上学期数学期末考试试卷上海市华东师范大学第二附属中学2023-2024学年高二上学期期末考试数学试卷四川省达州外国语学校2023-2024学年高二下学期期中质量监测数学试题河南省信阳市浉河区信阳高级中学北湖校区2024-2025学年高二上学期10月月考(一)数学试题河北省衡水市第十三中学2024届高三上学期质检三考试数学试题



