名校
1 . 设离散型随机变量X,Y的取值分别为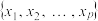 ,
,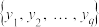
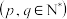 .定义X关于事件“
.定义X关于事件“ ”
”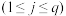 的条件数学期望为:
的条件数学期望为: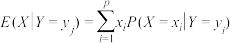 .已知条件数学期望满足全期望公式:
.已知条件数学期望满足全期望公式: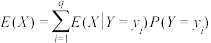 .解决如下问题:
.解决如下问题:
为了研究某药物对于微生物A生存状况的影响,某实验室计划进行生物实验.在第1天上午,实验人员向培养皿中加入10个A的个体.从第1天开始,实验人员在每天下午向培养皿中加入该种药物.当加入药物时,A的每个个体立即以相等的概率随机产生1次如下的生理反应(设A的每个个体在当天的其他时刻均不发生变化,不同个体的生理反应相互独立):
①直接死亡;②分裂为2个个体.
设第n天上午培养皿中A的个体数量为 .规定
.规定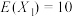 ,
,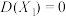 .
.
(1)求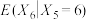 ;
;
(2)求 ;
;
(3)已知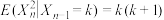
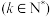 ,证明:
,证明: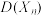 随着n的增大而增大.
随着n的增大而增大.
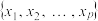 ,
,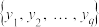
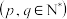 .定义X关于事件“
.定义X关于事件“ ”
”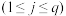 的条件数学期望为:
的条件数学期望为: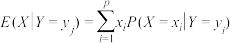 .已知条件数学期望满足全期望公式:
.已知条件数学期望满足全期望公式: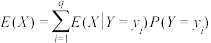 .解决如下问题:
.解决如下问题:为了研究某药物对于微生物A生存状况的影响,某实验室计划进行生物实验.在第1天上午,实验人员向培养皿中加入10个A的个体.从第1天开始,实验人员在每天下午向培养皿中加入该种药物.当加入药物时,A的每个个体立即以相等的概率随机产生1次如下的生理反应(设A的每个个体在当天的其他时刻均不发生变化,不同个体的生理反应相互独立):
①直接死亡;②分裂为2个个体.
设第n天上午培养皿中A的个体数量为
 .规定
.规定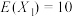 ,
,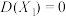 .
.(1)求
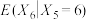 ;
;(2)求
 ;
;(3)已知
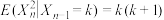
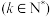 ,证明:
,证明: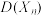 随着n的增大而增大.
随着n的增大而增大.
您最近一年使用:0次
名校
解题方法
2 . 新高考数学试卷出现多项选择题,即每小题的四个选项中,有多项符合题目要求,全部选对得6分,部分选对得部分分,有选错的得0分.若正确答案为两项,每对一项得3分:若正确答案为三项,每对一项得2分;
(1)学生甲在作答某题时,对四个选项作出正确判断、判断不了(不选)和错误判断的概率如下表:
若此题的正确选项为AC.求学生甲答此题得6分的概率:
(2)某数学小组研究发现,多选题正确答案是两个选项的概率为 ,正确答案是三个选项的概率为
,正确答案是三个选项的概率为 (
( ).现有一道多选题,学生乙完全不会,此时他有两种答题方案:Ⅰ.随机选一个选项;Ⅱ.随机选两个选项.
).现有一道多选题,学生乙完全不会,此时他有两种答题方案:Ⅰ.随机选一个选项;Ⅱ.随机选两个选项.
①若 ,且学生乙选择方案Ⅰ,分别求学生乙本题得0分、得2分的概率.
,且学生乙选择方案Ⅰ,分别求学生乙本题得0分、得2分的概率.
②以本题得分的数学期望为决策依据,p的取值在什么范围内唯独选择方案Ⅰ最好?
(1)学生甲在作答某题时,对四个选项作出正确判断、判断不了(不选)和错误判断的概率如下表:
| 选项 | 作出正确判断 | 判断不了(不选) | 作出错误判断 |
| A | 0.8 | 0.1 | 0.1 |
| B | 0.7 | 0.1 | 0.2 |
| C | 0.6 | 0.3 | 0.1 |
| D | 0.5 | 0.3 | 0.2 |
(2)某数学小组研究发现,多选题正确答案是两个选项的概率为
 ,正确答案是三个选项的概率为
,正确答案是三个选项的概率为 (
( ).现有一道多选题,学生乙完全不会,此时他有两种答题方案:Ⅰ.随机选一个选项;Ⅱ.随机选两个选项.
).现有一道多选题,学生乙完全不会,此时他有两种答题方案:Ⅰ.随机选一个选项;Ⅱ.随机选两个选项.①若
 ,且学生乙选择方案Ⅰ,分别求学生乙本题得0分、得2分的概率.
,且学生乙选择方案Ⅰ,分别求学生乙本题得0分、得2分的概率.②以本题得分的数学期望为决策依据,p的取值在什么范围内唯独选择方案Ⅰ最好?
您最近一年使用:0次
2024-09-26更新
|
986次组卷
|
2卷引用:广东省深圳市红岭中学(红岭教育集团)2025届高三上学期第一次统一考试数学试卷
解题方法
3 . 若数列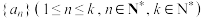 满足
满足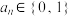 ,则称数列
,则称数列 为
为 项
项 数列,由所有
数列,由所有 项0
项0 数列组成集合
数列组成集合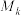 .
.
(1)若 是12项0
是12项0 数列,当且仅当
数列,当且仅当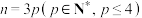 时,
时, ,求数列
,求数列 的所有项的和;
的所有项的和;
(2)从集合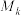 中任意取出两个数列
中任意取出两个数列 ,记
,记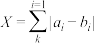 .
.
①求随机变量 的分布列,并证明:
的分布列,并证明: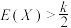 ;
;
②若用某软件产生 项
项 数列,记事件
数列,记事件 “第一次产生数字1”,
“第一次产生数字1”, “第二次产生数字1”,且
“第二次产生数字1”,且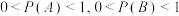 .若
.若 ,比较
,比较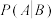 与
与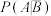 的大小.
的大小.
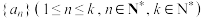 满足
满足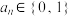 ,则称数列
,则称数列 为
为 项
项 数列,由所有
数列,由所有 项0
项0 数列组成集合
数列组成集合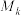 .
.(1)若
 是12项0
是12项0 数列,当且仅当
数列,当且仅当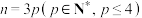 时,
时, ,求数列
,求数列 的所有项的和;
的所有项的和;(2)从集合
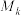 中任意取出两个数列
中任意取出两个数列 ,记
,记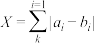 .
.①求随机变量
 的分布列,并证明:
的分布列,并证明: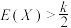 ;
;②若用某软件产生
 项
项 数列,记事件
数列,记事件 “第一次产生数字1”,
“第一次产生数字1”, “第二次产生数字1”,且
“第二次产生数字1”,且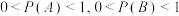 .若
.若 ,比较
,比较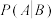 与
与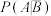 的大小.
的大小.
您最近一年使用:0次
名校
解题方法
4 . 在 维空间中
维空间中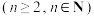 ,以单位长度为边长的“立方体”的顶点坐标可表示为
,以单位长度为边长的“立方体”的顶点坐标可表示为 维坐标
维坐标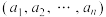 ,其中
,其中 .定义:在
.定义:在 维空间中两点
维空间中两点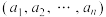 与
与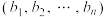 的曼哈顿距离为
的曼哈顿距离为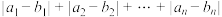 .在
.在 维“立方体”的顶点中任取两个不同的顶点,记随机变量
维“立方体”的顶点中任取两个不同的顶点,记随机变量 为所取两点间的曼哈顿距离,则
为所取两点间的曼哈顿距离,则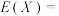
__________ .
 维空间中
维空间中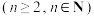 ,以单位长度为边长的“立方体”的顶点坐标可表示为
,以单位长度为边长的“立方体”的顶点坐标可表示为 维坐标
维坐标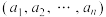 ,其中
,其中 .定义:在
.定义:在 维空间中两点
维空间中两点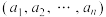 与
与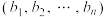 的曼哈顿距离为
的曼哈顿距离为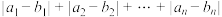 .在
.在 维“立方体”的顶点中任取两个不同的顶点,记随机变量
维“立方体”的顶点中任取两个不同的顶点,记随机变量 为所取两点间的曼哈顿距离,则
为所取两点间的曼哈顿距离,则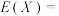
您最近一年使用:0次
2024-10-19更新
|
197次组卷
|
6卷引用:广东省广州市部分学校2025届高三第二次教学质量联合测评数学试题
广东省广州市部分学校2025届高三第二次教学质量联合测评数学试题上海市曹杨第二中学2023-2024学年高二下学期期末考试数学试卷(已下线)第三章 随机变量及其分布列 专题一 随机变量的期望 微点3 随机变量的分布列、期望综合训练【培优版】上海师范大学附属中学闵行分校2024-2025学年高三上学期9月月考数学试题(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点1 概率统计与数列交汇(一)【培优版】(已下线)第07讲 离散型随机变量及其分布列、数字特征(六大题型)(练习)
5 . 将4个面上分别写有数字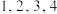 的一个正四面体在桌面上连续独立地抛
的一个正四面体在桌面上连续独立地抛 次(
次( 为正整数),设
为正整数),设 为与桌面接触的数字为偶数的次数,
为与桌面接触的数字为偶数的次数, 为抛正四面体一次与桌面接触的数字为偶数的概率.
为抛正四面体一次与桌面接触的数字为偶数的概率.
(1)当 时,若正四面体的质地是均匀的,求
时,若正四面体的质地是均匀的,求 的数学期望和方差;
的数学期望和方差;
(2)若正四面体有瑕疵,即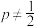 .
.
①设 是抛掷正四面体
是抛掷正四面体 次中与桌面接触的数字为偶数出现奇数次的概率,求证:
次中与桌面接触的数字为偶数出现奇数次的概率,求证: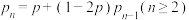 ;
;
②求抛掷正四面体 次中与桌面接触的数字为偶数出现偶数次的概率.
次中与桌面接触的数字为偶数出现偶数次的概率.
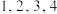 的一个正四面体在桌面上连续独立地抛
的一个正四面体在桌面上连续独立地抛 次(
次( 为正整数),设
为正整数),设 为与桌面接触的数字为偶数的次数,
为与桌面接触的数字为偶数的次数, 为抛正四面体一次与桌面接触的数字为偶数的概率.
为抛正四面体一次与桌面接触的数字为偶数的概率.(1)当
 时,若正四面体的质地是均匀的,求
时,若正四面体的质地是均匀的,求 的数学期望和方差;
的数学期望和方差;(2)若正四面体有瑕疵,即
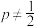 .
.①设
 是抛掷正四面体
是抛掷正四面体 次中与桌面接触的数字为偶数出现奇数次的概率,求证:
次中与桌面接触的数字为偶数出现奇数次的概率,求证: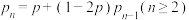 ;
;②求抛掷正四面体
 次中与桌面接触的数字为偶数出现偶数次的概率.
次中与桌面接触的数字为偶数出现偶数次的概率.
您最近一年使用:0次
6 . 马尔科夫链因俄国数学家安德烈・马尔科夫得名,其过程具备“无记忆”的性质,即第 次状态的概率分布只跟第
次状态的概率分布只跟第 次的状态有关,与第
次的状态有关,与第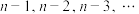 次状态无关.马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.现有
次状态无关.马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.现有 两个盒子,各装有2个黑球和1个红球,现从
两个盒子,各装有2个黑球和1个红球,现从 两个盒子中各任取一个球交换放入另一个盒子,重复进行
两个盒子中各任取一个球交换放入另一个盒子,重复进行 次这样的操作后,记
次这样的操作后,记 盒子中红球的个数为
盒子中红球的个数为 ,恰有1个红球的概率为
,恰有1个红球的概率为 .
.
(1)求 的值;
的值;
(2)求 的值(用
的值(用 表示);
表示);
(3)求证: 的数学期望
的数学期望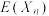 为定值.
为定值.
 次状态的概率分布只跟第
次状态的概率分布只跟第 次的状态有关,与第
次的状态有关,与第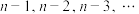 次状态无关.马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.现有
次状态无关.马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.现有 两个盒子,各装有2个黑球和1个红球,现从
两个盒子,各装有2个黑球和1个红球,现从 两个盒子中各任取一个球交换放入另一个盒子,重复进行
两个盒子中各任取一个球交换放入另一个盒子,重复进行 次这样的操作后,记
次这样的操作后,记 盒子中红球的个数为
盒子中红球的个数为 ,恰有1个红球的概率为
,恰有1个红球的概率为 .
.(1)求
 的值;
的值;(2)求
 的值(用
的值(用 表示);
表示);(3)求证:
 的数学期望
的数学期望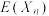 为定值.
为定值.
您最近一年使用:0次
2024-08-05更新
|
974次组卷
|
7卷引用:广东省八校2025届高三上学期8月联合检测数学试题
广东省八校2025届高三上学期8月联合检测数学试题(已下线)专题6 概率与统计中的新定义压轴大题(过关集训)(已下线)专题2 随机变量及其分布压轴大题(三)【讲】(已下线)第二章 概率 专题二 古典概型 微点2 古典概型(二)【培优版】(已下线)重难点突破03 高等背景下概率论新定义(七大题型)(已下线)阶段测4 周测12-周测13(高三一轮好卷针对提升卷)(已下线)第五章 概率统计创新问题 专题五 概率统计中的数学文化 微点3 概率统计中的数学文化综合训练【基础版】
名校
解题方法
7 . 某企业的设备控制系统由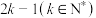 个相同的元件组成,每个元件正常工作的概率均为
个相同的元件组成,每个元件正常工作的概率均为 ,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为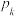 (例如:
(例如: 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).
(1)若 ,且每个元件正常工作的概率
,且每个元件正常工作的概率 .
.
①求控制系统中正常工作的元件个数X的分布列和期望;
②在设备正常运行的条件下,求所有元件都正常工作的概率.
(2)请用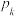 表示
表示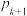 ,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
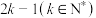 个相同的元件组成,每个元件正常工作的概率均为
个相同的元件组成,每个元件正常工作的概率均为 ,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为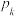 (例如:
(例如: 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).(1)若
 ,且每个元件正常工作的概率
,且每个元件正常工作的概率 .
.①求控制系统中正常工作的元件个数X的分布列和期望;
②在设备正常运行的条件下,求所有元件都正常工作的概率.
(2)请用
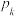 表示
表示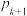 ,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
您最近一年使用:0次
2024-07-15更新
|
428次组卷
|
3卷引用:广东省广州市执信中学2023-2024学年高二下学期期末考试数学试卷
名校
解题方法
8 . 一个袋子中有30个大小相同的球,其中有10个红球、20个白球,从中随机有放回地逐次摸球作为样本,摸到红球或者第5次摸球之后停止.用 表示停止时摸球的次数.
表示停止时摸球的次数.
(1)求 的分布列和期望;
的分布列和期望;
(2)用样本中红球的比例估计总体中红球的比例,求误差的绝对值不超过 的概率.
的概率.
 表示停止时摸球的次数.
表示停止时摸球的次数.(1)求
 的分布列和期望;
的分布列和期望;(2)用样本中红球的比例估计总体中红球的比例,求误差的绝对值不超过
 的概率.
的概率.
您最近一年使用:0次
解题方法
9 . 某省高考自2024年起数学考试多选题(题号9~11)的计分标准是:每道题满分6分,全部选对得6分,部分选对得部分分(若某道题正确选项为两个,漏选一个正确选项得3分;若某道题正确选项为三个,漏选一个正确选项得4分,漏选两个正确选项得2分),错选或不选得0分.每道多选题共4个选项,正确答案是选两项或选三项.统计规律显示:多选题正确答案是“选两项”的概率是 ,没有同学选四项.甲、乙两个同学参加了考前模拟测试,已知两同学第9题选的全对,第10~11题还不确定对错.
,没有同学选四项.甲、乙两个同学参加了考前模拟测试,已知两同学第9题选的全对,第10~11题还不确定对错.
(1)假设甲同学第10题随机选了两个选项,第11题随机选了一个选项,求甲同学这三道多选题(满分18分)所有可能总得分的中位数;
(2)假设第10题正确答案是“选两项”,若乙同学不知道是“选两项”,随机选该题的选项(既没空选也没选四项,所有选法等可能),求乙第10题得0分的概率 ;
;
(3)第11题甲同学采用“随机猜一个选项”的答题策略,乙同学采用“随机猜两个选项”的答题策略,记甲同学该题的得分为X,乙同学该题的得分为Y,试比较两同学得分的平均值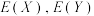 的大小.
的大小.
 ,没有同学选四项.甲、乙两个同学参加了考前模拟测试,已知两同学第9题选的全对,第10~11题还不确定对错.
,没有同学选四项.甲、乙两个同学参加了考前模拟测试,已知两同学第9题选的全对,第10~11题还不确定对错.(1)假设甲同学第10题随机选了两个选项,第11题随机选了一个选项,求甲同学这三道多选题(满分18分)所有可能总得分的中位数;
(2)假设第10题正确答案是“选两项”,若乙同学不知道是“选两项”,随机选该题的选项(既没空选也没选四项,所有选法等可能),求乙第10题得0分的概率
 ;
;(3)第11题甲同学采用“随机猜一个选项”的答题策略,乙同学采用“随机猜两个选项”的答题策略,记甲同学该题的得分为X,乙同学该题的得分为Y,试比较两同学得分的平均值
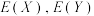 的大小.
的大小.
您最近一年使用:0次
解题方法
10 . 某同学参加趣味答题比赛,规则如下:第1次答题时,若答对则得2分,否则得1分;从第2次答题开始,若答对则获得上一次答题得分的2倍,否则得1分,该同学每次答对的概率都为 ,答错的概率都为
,答错的概率都为 ,且每次答对与否相互独立.记第
,且每次答对与否相互独立.记第 次答题得分为
次答题得分为 .
.
(1)求 ;
;
(2)求 (
( )的分布列和期望;
)的分布列和期望;
(3)在游戏开始前,该同学有两个选择,①从第2次开始,若第 次得分刚好为
次得分刚好为 时,则该同学获得胜利,游戏结束.②从第1次开始,若第
时,则该同学获得胜利,游戏结束.②从第1次开始,若第 次得分刚好为
次得分刚好为 时,则该同学获得胜利,游戏结束.已知共有4次答题环节,求该同学选择哪个方案获得胜利的概率更大.
时,则该同学获得胜利,游戏结束.已知共有4次答题环节,求该同学选择哪个方案获得胜利的概率更大.
 ,答错的概率都为
,答错的概率都为 ,且每次答对与否相互独立.记第
,且每次答对与否相互独立.记第 次答题得分为
次答题得分为 .
.(1)求
 ;
;(2)求
 (
( )的分布列和期望;
)的分布列和期望;(3)在游戏开始前,该同学有两个选择,①从第2次开始,若第
 次得分刚好为
次得分刚好为 时,则该同学获得胜利,游戏结束.②从第1次开始,若第
时,则该同学获得胜利,游戏结束.②从第1次开始,若第 次得分刚好为
次得分刚好为 时,则该同学获得胜利,游戏结束.已知共有4次答题环节,求该同学选择哪个方案获得胜利的概率更大.
时,则该同学获得胜利,游戏结束.已知共有4次答题环节,求该同学选择哪个方案获得胜利的概率更大.
您最近一年使用:0次



