解题方法
1 . 若数列 (
( )满足
)满足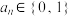 ,则称数列
,则称数列 为
为 项
项 数列,由所有
数列,由所有 项
项 数列组成集合
数列组成集合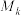 .
.
(1)若 是100项
是100项 数列,当且仅当
数列,当且仅当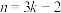 (
( ,
,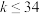 )时,
)时, ,求数列
,求数列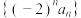 的所有项的和;
的所有项的和;
(2)从集合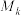 中任意取出两个数列
中任意取出两个数列 ,
, ,记
,记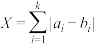 .
.
①求 的分布列,并证明
的分布列,并证明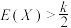 ;
;
②若用某软件产生 项
项 数列,记事件
数列,记事件 “第一次产生数字1”,
“第一次产生数字1”, “第二次产生数字1”,若
“第二次产生数字1”,若 ,比较
,比较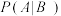 与
与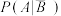 的大小.
的大小.
 (
( )满足
)满足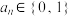 ,则称数列
,则称数列 为
为 项
项 数列,由所有
数列,由所有 项
项 数列组成集合
数列组成集合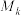 .
.(1)若
 是100项
是100项 数列,当且仅当
数列,当且仅当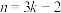 (
( ,
,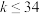 )时,
)时, ,求数列
,求数列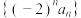 的所有项的和;
的所有项的和;(2)从集合
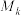 中任意取出两个数列
中任意取出两个数列 ,
, ,记
,记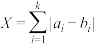 .
.①求
 的分布列,并证明
的分布列,并证明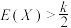 ;
;②若用某软件产生
 项
项 数列,记事件
数列,记事件 “第一次产生数字1”,
“第一次产生数字1”, “第二次产生数字1”,若
“第二次产生数字1”,若 ,比较
,比较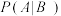 与
与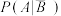 的大小.
的大小.
您最近一年使用:0次
2 . 已知三个正整数的和为8,用 表示这三个数中最小的数,则
表示这三个数中最小的数,则 的期望
的期望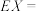
__________ .
 表示这三个数中最小的数,则
表示这三个数中最小的数,则 的期望
的期望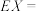
您最近一年使用:0次
2024-07-22更新
|
405次组卷
|
2卷引用:湖南省长沙市六校2025届高三上学期八月开学联合检测数学试题
3 . 将数字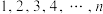 任意排成一列,如果数字
任意排成一列,如果数字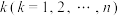 恰好在第
恰好在第 个位置上,则称有一个巧合,巧合的个数称为巧合数,记为
个位置上,则称有一个巧合,巧合的个数称为巧合数,记为 .例如
.例如 时,2,1,3,4为可能的一个排列,此时
时,2,1,3,4为可能的一个排列,此时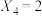 .
.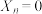 的排列称为全错位排列,并记数字
的排列称为全错位排列,并记数字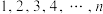 的全错位排列种数为
的全错位排列种数为 .
.
(1)写出 的值,并求
的值,并求 的分布列;
的分布列;
(2)求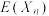 ;
;
(3)求 .
.
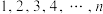 任意排成一列,如果数字
任意排成一列,如果数字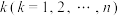 恰好在第
恰好在第 个位置上,则称有一个巧合,巧合的个数称为巧合数,记为
个位置上,则称有一个巧合,巧合的个数称为巧合数,记为 .例如
.例如 时,2,1,3,4为可能的一个排列,此时
时,2,1,3,4为可能的一个排列,此时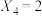 .
.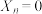 的排列称为全错位排列,并记数字
的排列称为全错位排列,并记数字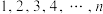 的全错位排列种数为
的全错位排列种数为 .
.(1)写出
 的值,并求
的值,并求 的分布列;
的分布列;(2)求
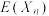 ;
;(3)求
 .
.
您最近一年使用:0次
名校
解题方法
4 . 某企业的设备控制系统由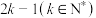 个相同的元件组成,每个元件正常工作的概率均为
个相同的元件组成,每个元件正常工作的概率均为 ,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为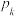 (例如:
(例如: 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).
(1)若 ,且每个元件正常工作的概率
,且每个元件正常工作的概率 .
.
①求控制系统中正常工作的元件个数X的分布列和期望;
②在设备正常运行的条件下,求所有元件都正常工作的概率.
(2)请用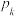 表示
表示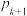 ,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
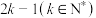 个相同的元件组成,每个元件正常工作的概率均为
个相同的元件组成,每个元件正常工作的概率均为 ,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
,各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为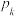 (例如:
(例如: 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).(1)若
 ,且每个元件正常工作的概率
,且每个元件正常工作的概率 .
.①求控制系统中正常工作的元件个数X的分布列和期望;
②在设备正常运行的条件下,求所有元件都正常工作的概率.
(2)请用
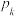 表示
表示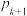 ,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
,并探究:在确保控制系统中元件总数为奇数的前提下,能否通过增加控制系统中元件的个数来提高设备正常运行的概率.
您最近一年使用:0次
2024-07-15更新
|
428次组卷
|
3卷引用:湖南省长沙市六校2025届高三上学期八月开学联合检测数学试题
名校
5 . 第二次世界大战期间,了解德军坦克的生产能力对盟军具有非常重要的战略意义.已知德军的每辆坦克上都有一个按生产顺序从1开始的连续编号.假设德军某月生产的坦克总数为N,随机缴获该月生产的n辆( )坦克的编号为
)坦克的编号为 ,
, ,…,
,…, ,记
,记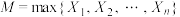 ,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
甲同学根据样本均值估计总体均值的思想,用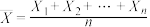 估计总体的均值,因此
估计总体的均值,因此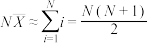 ,得
,得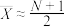 ,故可用
,故可用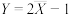 作为N的估计.
作为N的估计.
乙同学对此提出异议,认为这种方法可能出现 的无意义结果.例如,当
的无意义结果.例如,当 ,
, 时,若
时,若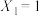 ,
,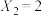 ,
,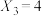 ,则
,则 ,此时
,此时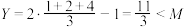 .
.
(1)当 ,
, 时,求条件概率
时,求条件概率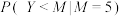 ;
;
(2)为了避免甲同学方法的缺点,乙同学提出直接用M作为N的估计值.当 ,
, 时,求随机变量M的分布列和均值
时,求随机变量M的分布列和均值 ;
;
(3)丙同学认为估计值的均值应稳定于实际值,但直观上可以发现 与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断
与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断 与N的大小关系,并给出证明.
与N的大小关系,并给出证明.
 )坦克的编号为
)坦克的编号为 ,
, ,…,
,…, ,记
,记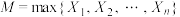 ,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.甲同学根据样本均值估计总体均值的思想,用
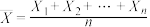 估计总体的均值,因此
估计总体的均值,因此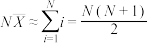 ,得
,得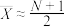 ,故可用
,故可用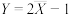 作为N的估计.
作为N的估计.乙同学对此提出异议,认为这种方法可能出现
 的无意义结果.例如,当
的无意义结果.例如,当 ,
, 时,若
时,若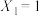 ,
,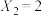 ,
,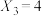 ,则
,则 ,此时
,此时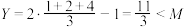 .
.(1)当
 ,
, 时,求条件概率
时,求条件概率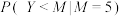 ;
;(2)为了避免甲同学方法的缺点,乙同学提出直接用M作为N的估计值.当
 ,
, 时,求随机变量M的分布列和均值
时,求随机变量M的分布列和均值 ;
;(3)丙同学认为估计值的均值应稳定于实际值,但直观上可以发现
 与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断
与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断 与N的大小关系,并给出证明.
与N的大小关系,并给出证明.
您最近一年使用:0次
2024-05-28更新
|
1145次组卷
|
4卷引用:湖南省长沙市长郡中学2023-2024学年高三下学期保温卷一数学试题
名校
6 . 为应对新一代小型无人机武器,某研发部门开发了甲、乙两种不同的防御武器,现对两种武器的防御效果进行测试.每次测试都是由一种武器向目标无人机发动三次攻击,每次攻击击中目标与否相互独立,每次测试都会使用性能一样的全新无人机.对于甲种武器,每次攻击击中目标无人机的概率均为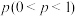 ,且击中一次目标无人机坠毁的概率为
,且击中一次目标无人机坠毁的概率为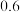 ,击中两次目标无人机必坠毁;对于乙种武器,每次攻击击中目标无人机的概率均为
,击中两次目标无人机必坠毁;对于乙种武器,每次攻击击中目标无人机的概率均为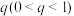 ,且击中一次目标无人机坠毁的概率为
,且击中一次目标无人机坠毁的概率为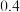 ,击中两次目标无人机坠毁的概率为
,击中两次目标无人机坠毁的概率为 ,击中三次目标无人机必坠毁.
,击中三次目标无人机必坠毁.
(1)若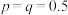 ,分别使用甲、乙两种武器进行一次测试.
,分别使用甲、乙两种武器进行一次测试.
①求甲种武器使目标无人机坠毁的概率;
②记甲、乙两种武器使目标无人机坠毁的数量为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
(2)若 ,且
,且 ,试判断在一次测试中选用甲种武器还是乙种武器使得目标无人机坠毁的概率更大?并说明理由.
,试判断在一次测试中选用甲种武器还是乙种武器使得目标无人机坠毁的概率更大?并说明理由.
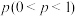 ,且击中一次目标无人机坠毁的概率为
,且击中一次目标无人机坠毁的概率为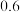 ,击中两次目标无人机必坠毁;对于乙种武器,每次攻击击中目标无人机的概率均为
,击中两次目标无人机必坠毁;对于乙种武器,每次攻击击中目标无人机的概率均为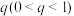 ,且击中一次目标无人机坠毁的概率为
,且击中一次目标无人机坠毁的概率为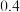 ,击中两次目标无人机坠毁的概率为
,击中两次目标无人机坠毁的概率为 ,击中三次目标无人机必坠毁.
,击中三次目标无人机必坠毁.(1)若
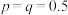 ,分别使用甲、乙两种武器进行一次测试.
,分别使用甲、乙两种武器进行一次测试.①求甲种武器使目标无人机坠毁的概率;
②记甲、乙两种武器使目标无人机坠毁的数量为
 ,求
,求 的分布列与数学期望.
的分布列与数学期望.(2)若
 ,且
,且 ,试判断在一次测试中选用甲种武器还是乙种武器使得目标无人机坠毁的概率更大?并说明理由.
,试判断在一次测试中选用甲种武器还是乙种武器使得目标无人机坠毁的概率更大?并说明理由.
您最近一年使用:0次
2024-05-24更新
|
959次组卷
|
4卷引用:湖南省岳阳市岳阳县第一中学2023-2024学年高二下学期6月月考数学试题
名校
解题方法
7 . 二项分布是离散型随机变量重要的概率模型,在生活中被广泛应用.现在我们来研究二项分布的简单性质,若随机变量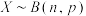 .
.
(1)证明:(ⅰ)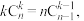 (
( ,且
,且 ),其中
),其中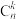 为组合数;
为组合数;
(ⅱ)随机变量 的数学期望
的数学期望 ;
;
(2)一盒中有形状大小相同的4个白球和3个黑球,每次从中摸出一个球且不放回,直到摸到黑球为止,记事件A表示第二次摸球时首次摸到黑球,若将上述试验重复进行10次,记随机变量 表示事件A发生的次数,试探求
表示事件A发生的次数,试探求 的值与随机变量
的值与随机变量 最有可能发生次数的大小关系.
最有可能发生次数的大小关系.
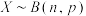 .
.(1)证明:(ⅰ)
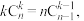 (
( ,且
,且 ),其中
),其中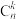 为组合数;
为组合数;(ⅱ)随机变量
 的数学期望
的数学期望 ;
;(2)一盒中有形状大小相同的4个白球和3个黑球,每次从中摸出一个球且不放回,直到摸到黑球为止,记事件A表示第二次摸球时首次摸到黑球,若将上述试验重复进行10次,记随机变量
 表示事件A发生的次数,试探求
表示事件A发生的次数,试探求 的值与随机变量
的值与随机变量 最有可能发生次数的大小关系.
最有可能发生次数的大小关系.
您最近一年使用:0次
2024-05-12更新
|
404次组卷
|
4卷引用:湖南省湖湘教育三新探索协作体2023-2024学年高二下学期期中联考数学试题
湖南省湖湘教育三新探索协作体2023-2024学年高二下学期期中联考数学试题(已下线)第27题 二项分布(高二期末每日一题)山东省泰安市部分学校2023-2024学年高二下学期期末测试数学试题(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点3 重要的概率分布模型综合训练【基础版】
名校
解题方法
8 . 投掷一枚均匀的骰子,每次掷得的点数为5或6时得2分,掷得的点数为1,2,3,4时得1分,独立地重复掷一枚骰子,将每次得分相加的结果作为最终得分.
(1)设投掷2次骰子,最终得分为X,求随机变量X的分布列与期望;
(2)记n次抛掷得分恰为 分的概率为
分的概率为 ,求
,求 的前n项和
的前n项和 ;
;
(3)投掷骰子100次,记得分恰为n分的概率为 ,当
,当 取最大值时,求n的值.
取最大值时,求n的值.
(1)设投掷2次骰子,最终得分为X,求随机变量X的分布列与期望;
(2)记n次抛掷得分恰为
 分的概率为
分的概率为 ,求
,求 的前n项和
的前n项和 ;
;(3)投掷骰子100次,记得分恰为n分的概率为
 ,当
,当 取最大值时,求n的值.
取最大值时,求n的值.
您最近一年使用:0次
2024-05-11更新
|
637次组卷
|
3卷引用:湖南师范大学附属中学2023-2024学年高二下学期期中考试数学试题
湖南师范大学附属中学2023-2024学年高二下学期期中考试数学试题(已下线)专题07 概率与统计综合问题(6类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)江苏省宿迁市泗阳县两校2023-2024学年高二下学期第二次学情调研(5月月考)数学试题
名校
解题方法
9 . 某大学有甲、乙两个运动场.假设同学们可以任意选择其中一个运动场锻炼,也可选择不锻炼,一天最多锻炼一次,一次只能选择一个运动场.若同学们每次锻炼选择去甲或乙运动场的概率均为 ,每次选择相互独立.设王同学在某个假期的三天内去运动场锻炼的次数为
,每次选择相互独立.设王同学在某个假期的三天内去运动场锻炼的次数为 ,已知
,已知 的分布列如下:(其中
的分布列如下:(其中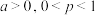 )
)
(1)记事件 表示王同学假期三天内去运动场锻炼
表示王同学假期三天内去运动场锻炼 次
次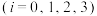 ,事件
,事件 表示王同学在这三天内去甲运动场锻炼的次数大于去乙运动场锻炼的次数.当
表示王同学在这三天内去甲运动场锻炼的次数大于去乙运动场锻炼的次数.当 时,试根据全概率公式求
时,试根据全概率公式求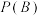 的值;
的值;
(2)是否存在实数 ,使得
,使得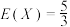 ?若存在,求
?若存在,求 的值:若不存在,请说明理由;
的值:若不存在,请说明理由;
(3)记 表示事件“甲运动场举办锻炼有奖的抽奖活动”,
表示事件“甲运动场举办锻炼有奖的抽奖活动”, 表示事件“王同学去甲运动场锻炼”,
表示事件“王同学去甲运动场锻炼”,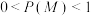 .已知王同学在甲运动场举办锻炼有奖的抽奖活动的情况下去甲运动场锻炼的概率,比不举办抽奖活动的情况下去甲运动场锻炼的概率大,证明:
.已知王同学在甲运动场举办锻炼有奖的抽奖活动的情况下去甲运动场锻炼的概率,比不举办抽奖活动的情况下去甲运动场锻炼的概率大,证明: .
.
 ,每次选择相互独立.设王同学在某个假期的三天内去运动场锻炼的次数为
,每次选择相互独立.设王同学在某个假期的三天内去运动场锻炼的次数为 ,已知
,已知 的分布列如下:(其中
的分布列如下:(其中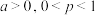 )
) | 0 | 1 | 2 | 3 |
 | 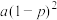 | 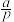 |  |  |
 表示王同学假期三天内去运动场锻炼
表示王同学假期三天内去运动场锻炼 次
次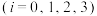 ,事件
,事件 表示王同学在这三天内去甲运动场锻炼的次数大于去乙运动场锻炼的次数.当
表示王同学在这三天内去甲运动场锻炼的次数大于去乙运动场锻炼的次数.当 时,试根据全概率公式求
时,试根据全概率公式求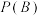 的值;
的值;(2)是否存在实数
 ,使得
,使得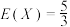 ?若存在,求
?若存在,求 的值:若不存在,请说明理由;
的值:若不存在,请说明理由;(3)记
 表示事件“甲运动场举办锻炼有奖的抽奖活动”,
表示事件“甲运动场举办锻炼有奖的抽奖活动”, 表示事件“王同学去甲运动场锻炼”,
表示事件“王同学去甲运动场锻炼”,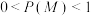 .已知王同学在甲运动场举办锻炼有奖的抽奖活动的情况下去甲运动场锻炼的概率,比不举办抽奖活动的情况下去甲运动场锻炼的概率大,证明:
.已知王同学在甲运动场举办锻炼有奖的抽奖活动的情况下去甲运动场锻炼的概率,比不举办抽奖活动的情况下去甲运动场锻炼的概率大,证明: .
.
您最近一年使用:0次
2024-05-04更新
|
1523次组卷
|
3卷引用:湖南师范大学附属中学2024届高三下学期模拟(二)数学试卷
湖南师范大学附属中学2024届高三下学期模拟(二)数学试卷(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)浙江省温州市平阳县万全综合高级中学2023-2024学年中职高二下学期期末普高数学试题
名校
解题方法
10 . 某自然保护区经过几十年的发展,某种濒临灭绝动物数量有大幅度的增加.已知这种动物 拥有两个亚种(分别记为
拥有两个亚种(分别记为 种和
种和 种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物
种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物 ,统计其中
,统计其中 种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第
种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第 次试验中
次试验中 种的数目为随机变量
种的数目为随机变量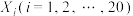 .设该区域中
.设该区域中 种的数目为
种的数目为 ,
, 种的数目为
种的数目为 (
( ,
, 均大于100),每一次试验均相互独立.
均大于100),每一次试验均相互独立.
(1)求 的分布列;
的分布列;
(2)记随机变量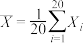 .已知
.已知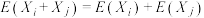 ,
,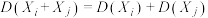
(i)证明: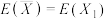 ,
,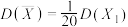 ;
;
(ii)该小组完成所有试验后,得到 的实际取值分别为
的实际取值分别为 .数据
.数据 的平均值
的平均值 ,方差
,方差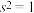 .采用
.采用 和
和 分别代替
分别代替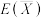 和
和 ,给出
,给出 ,
, 的估计值.
的估计值.
(已知随机变量 服从超几何分布记为:
服从超几何分布记为: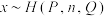 (其中
(其中 为总数,
为总数, 为某类元素的个数,
为某类元素的个数, 为抽取的个数),则
为抽取的个数),则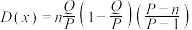 )
)
 拥有两个亚种(分别记为
拥有两个亚种(分别记为 种和
种和 种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物
种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物 ,统计其中
,统计其中 种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第
种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第 次试验中
次试验中 种的数目为随机变量
种的数目为随机变量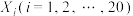 .设该区域中
.设该区域中 种的数目为
种的数目为 ,
, 种的数目为
种的数目为 (
( ,
, 均大于100),每一次试验均相互独立.
均大于100),每一次试验均相互独立.(1)求
 的分布列;
的分布列;(2)记随机变量
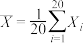 .已知
.已知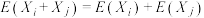 ,
,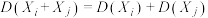
(i)证明:
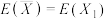 ,
,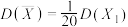 ;
;(ii)该小组完成所有试验后,得到
 的实际取值分别为
的实际取值分别为 .数据
.数据 的平均值
的平均值 ,方差
,方差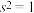 .采用
.采用 和
和 分别代替
分别代替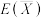 和
和 ,给出
,给出 ,
, 的估计值.
的估计值.(已知随机变量
 服从超几何分布记为:
服从超几何分布记为: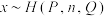 (其中
(其中 为总数,
为总数, 为某类元素的个数,
为某类元素的个数, 为抽取的个数),则
为抽取的个数),则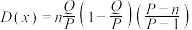 )
)
您最近一年使用:0次
2024-04-24更新
|
1919次组卷
|
4卷引用:湖南省2024届高考数学临门押题考试试卷
湖南省2024届高考数学临门押题考试试卷2024届辽宁省辽宁省高三重点高中协作校联考模拟预测数学试题(已下线)8.4 离散型随机变量的分布列,期望与方差(高考真题素材之十年高考)(已下线)专题2 随机变量及其分布压轴大题(过关集训)



