1 . 已知函数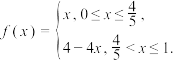 随机变量
随机变量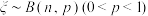 ,随机变量
,随机变量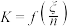 ,
, 的期望为
的期望为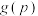 .
.
(1)当 时,求
时,求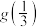 ;
;
(2)当 时,求
时,求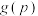 的表达式.
的表达式.
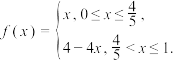 随机变量
随机变量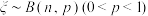 ,随机变量
,随机变量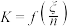 ,
, 的期望为
的期望为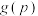 .
.(1)当
 时,求
时,求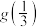 ;
;(2)当
 时,求
时,求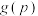 的表达式.
的表达式.
您最近一年使用:0次
2024-06-16更新
|
436次组卷
|
4卷引用:内蒙古自治区锡林郭勒盟2024届高三下学期5月模拟考试理科数学试题
内蒙古自治区锡林郭勒盟2024届高三下学期5月模拟考试理科数学试题河南省部分重点高中2023-2024学年高三下学期5月联考数学试卷 (新高考)(已下线)辽宁省沈阳市第二中学2024届高三下学期三模数学试题(已下线)概率、随机变量及其分布-综合测试卷B卷
解题方法
2 . 某数学兴趣小组模拟“刮刮乐”彩票游戏,每张彩票的刮奖区印有从10个数字1,2,3,…,10中随机抽取的3个不同数字,刮开涂层即可兑奖,中奖规则为:每张奖卷只能中奖一次(按照最高奖励算)若3个数的积为3的倍数且不为5的倍数时,中三等奖;若3个数的积为5的倍数且不为3的倍数时,中二等奖;若3个数的积既为3的倍数,又为4的倍数,又为7的倍数时,中一等奖;其他情况不中奖.
(1)随机抽取一张彩票,求这张彩票中奖的概率;
(2)假设每张彩票售价为 元,且获得三、二、一等奖的奖金分别为5元,10元,50元,从出售该彩票可获利的角度考虑,求
元,且获得三、二、一等奖的奖金分别为5元,10元,50元,从出售该彩票可获利的角度考虑,求 的最小值.
的最小值.
(1)随机抽取一张彩票,求这张彩票中奖的概率;
(2)假设每张彩票售价为
 元,且获得三、二、一等奖的奖金分别为5元,10元,50元,从出售该彩票可获利的角度考虑,求
元,且获得三、二、一等奖的奖金分别为5元,10元,50元,从出售该彩票可获利的角度考虑,求 的最小值.
的最小值.
您最近一年使用:0次
2024-02-29更新
|
1980次组卷
|
6卷引用:内蒙古赤峰第四中桥北学分校2024届高三下学期开学摸底联考数学(理)试题
2023高三·全国·专题练习
名校
解题方法
3 . 非物质文化遗产是一个国家和民族历史文化成就的重要标志,是优秀传统文化的重要组成部分.瑞昌剪纸于2008年列入第二批国家级非物质文化遗产名录.由于瑞昌地处南北交汇处,经过千年的南北文化相互浸润与渗透,瑞昌剪纸融入了南方的阴柔之丽、精巧秀美和北方的阳刚之美、古朴豪放.为了弘扬中国优秀的传统文化,某校将举办一次剪纸比赛,共进行5轮比赛,每轮比赛结果互不影响.比赛规则如下:每一轮比赛中,参赛者在30分钟内完成规定作品和创意作品各2幅,若有不少于3幅作品入选,将获得“巧手奖”.5轮比赛中,至少获得4次“巧手奖”的同学将进入决赛.某同学经历多次模拟训练,指导老师从训练作品中随机抽取规定作品和创意作品各5幅,其中有4幅规定作品和3幅创意作品符合入选标准.
(1)从这10幅训练作品中,随机抽取规定作品和创意作品各2幅,试预测该同学在一轮比赛中获“巧手奖”的概率;
(2)以上述两类作品各自入选的频率作为该同学参赛时每幅作品入选的概率.经指导老师对该同学进行赛前强化训练,规定作品和创意作品入选的概率共提高了 ,以获得“巧手奖”的次数期望为参考,试预测该同学能否进入决赛?
,以获得“巧手奖”的次数期望为参考,试预测该同学能否进入决赛?
(1)从这10幅训练作品中,随机抽取规定作品和创意作品各2幅,试预测该同学在一轮比赛中获“巧手奖”的概率;
(2)以上述两类作品各自入选的频率作为该同学参赛时每幅作品入选的概率.经指导老师对该同学进行赛前强化训练,规定作品和创意作品入选的概率共提高了
 ,以获得“巧手奖”的次数期望为参考,试预测该同学能否进入决赛?
,以获得“巧手奖”的次数期望为参考,试预测该同学能否进入决赛?
您最近一年使用:0次
2023-03-12更新
|
945次组卷
|
7卷引用:内蒙古自治区赤峰市赤峰第四中学2023-2024学年高二下学期5月月考(期中)数学试题
内蒙古自治区赤峰市赤峰第四中学2023-2024学年高二下学期5月月考(期中)数学试题(已下线)大题强化训练(9)(已下线)第07讲 二项分布与超几何分布及正态分布(核心考点讲与练)(2)江苏省南京市2024届高三上学期期末数学复习综合卷试题江苏省镇江市扬中市第二高级中学2023-2024学年高三上学期期末模拟数学试题3浙江省金华市曙光学校2023-2024学年高二下学期4月月考数学试题(已下线)第三章 随机变量及其分布列 专题四 随机变量分布列、期望、方差的应用 微点1 概率分布在生活、生产实践中的应用(一)【培优版】
4 . 检验中心为筛查某种疾病,需要检验血液是否为阳性,对 份血液样本,有以下两种检验方式:①逐份检验,需要检验
份血液样本,有以下两种检验方式:①逐份检验,需要检验 次;②混合检验,即将其中
次;②混合检验,即将其中 (
( 且
且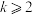 )份血液样本分别取样混合在一起检验,若检验结果为阴性,这
)份血液样本分别取样混合在一起检验,若检验结果为阴性,这 份的血液全为阴性,因而这
份的血液全为阴性,因而这 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这 份血液究竟哪几份为阳性,再对这
份血液究竟哪几份为阳性,再对这 份再逐份检验,此时这
份再逐份检验,此时这 份血液的检验次数总共为
份血液的检验次数总共为 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为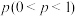 .
.
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中 (
( 且
且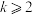 )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为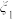 ,采用混合检验方式,样本需要检验的总次数为点
,采用混合检验方式,样本需要检验的总次数为点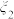 .当
.当 时,根据
时,根据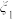 和
和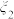 的期望值大小,讨论当
的期望值大小,讨论当 取何值时,采用逐份检验方式好?
取何值时,采用逐份检验方式好?
(参考数据: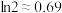 ,
,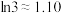 ,
,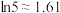 ,
,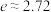 ,
, ,
, .)
.)
 份血液样本,有以下两种检验方式:①逐份检验,需要检验
份血液样本,有以下两种检验方式:①逐份检验,需要检验 次;②混合检验,即将其中
次;②混合检验,即将其中 (
( 且
且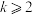 )份血液样本分别取样混合在一起检验,若检验结果为阴性,这
)份血液样本分别取样混合在一起检验,若检验结果为阴性,这 份的血液全为阴性,因而这
份的血液全为阴性,因而这 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这 份血液究竟哪几份为阳性,再对这
份血液究竟哪几份为阳性,再对这 份再逐份检验,此时这
份再逐份检验,此时这 份血液的检验次数总共为
份血液的检验次数总共为 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为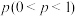 .
.(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中
 (
( 且
且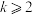 )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为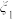 ,采用混合检验方式,样本需要检验的总次数为点
,采用混合检验方式,样本需要检验的总次数为点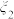 .当
.当 时,根据
时,根据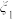 和
和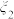 的期望值大小,讨论当
的期望值大小,讨论当 取何值时,采用逐份检验方式好?
取何值时,采用逐份检验方式好?(参考数据:
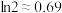 ,
,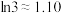 ,
,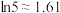 ,
,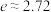 ,
, ,
, .)
.)
您最近一年使用:0次



