名校
解题方法
1 . 哈三中2024-2025年度上学期高二年级十月月考中有这样一道题目:已知A,B是两个随机事件,且 ,给出5个命题如下:
,给出5个命题如下:
①若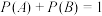 ,则事件A,B对立;
,则事件A,B对立;
②若事件A与B独立,则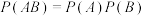 成立;
成立;
③若 ,则事件A,B相互独立,且
,则事件A,B相互独立,且 ;
;
若老师说某考生在5个命题中任选两个命题,其中真命题的个数 的方差为
的方差为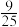 ,则④⑤中真命题的个数为
,则④⑤中真命题的个数为___________ .
 ,给出5个命题如下:
,给出5个命题如下:①若
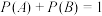 ,则事件A,B对立;
,则事件A,B对立;②若事件A与B独立,则
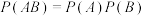 成立;
成立;③若
 ,则事件A,B相互独立,且
,则事件A,B相互独立,且 ;
;
若老师说某考生在5个命题中任选两个命题,其中真命题的个数
 的方差为
的方差为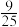 ,则④⑤中真命题的个数为
,则④⑤中真命题的个数为
您最近一年使用:0次
名校
2 . 随着新中考英语人机测试的推行,为了确保学生能够有效应对这一新的考试形式,某中学决定展开深入调查,组织一次模拟测试,对学生的英语水平能力进行准确评估,并据此制定针对性的教学方案.该校从初二学年学生中随机抽取40人将进行模拟测试.现将40人分成 三个小组,其中
三个小组,其中 组15人,
组15人, 组15人,
组15人, 组10人.
组10人.
(1)第一轮测试按小组 顺次进行.若一切正常,则该小组完成测试的时间为10分钟,若出现异常情况,则该小组需要延长5分钟才能完成测试.已知每小组正常完成测试的概率均为
顺次进行.若一切正常,则该小组完成测试的时间为10分钟,若出现异常情况,则该小组需要延长5分钟才能完成测试.已知每小组正常完成测试的概率均为 ,且各小组是否正常完成测试互不影响.记3个小组完成测试所需时间为
,且各小组是否正常完成测试互不影响.记3个小组完成测试所需时间为 ,求
,求 的分布列;
的分布列;
(2)第二轮测试将3组同学一起排序,每一位同学顺次上机操作.
①求最后一名同学来自 组的条件下,
组的条件下, 组同学比
组同学比 组同学提前完成测试的概率;
组同学提前完成测试的概率;
②若每名同学完成测试的时间都是为3分钟,求 组和
组和 组同学全部完成测试所需时间的期望.
组同学全部完成测试所需时间的期望.
 三个小组,其中
三个小组,其中 组15人,
组15人, 组15人,
组15人, 组10人.
组10人.(1)第一轮测试按小组
 顺次进行.若一切正常,则该小组完成测试的时间为10分钟,若出现异常情况,则该小组需要延长5分钟才能完成测试.已知每小组正常完成测试的概率均为
顺次进行.若一切正常,则该小组完成测试的时间为10分钟,若出现异常情况,则该小组需要延长5分钟才能完成测试.已知每小组正常完成测试的概率均为 ,且各小组是否正常完成测试互不影响.记3个小组完成测试所需时间为
,且各小组是否正常完成测试互不影响.记3个小组完成测试所需时间为 ,求
,求 的分布列;
的分布列;(2)第二轮测试将3组同学一起排序,每一位同学顺次上机操作.
①求最后一名同学来自
 组的条件下,
组的条件下, 组同学比
组同学比 组同学提前完成测试的概率;
组同学提前完成测试的概率;②若每名同学完成测试的时间都是为3分钟,求
 组和
组和 组同学全部完成测试所需时间的期望.
组同学全部完成测试所需时间的期望.
您最近一年使用:0次
名校
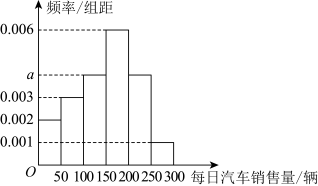
3 . 某汽车销售公司为了提升公司的业绩,现将最近300个工作日每日的汽车销售情况进行统计,如图所示. 的值以及该公司这300个工作日每日汽车销售量的平均数(同一组中的数据用该组区间的中点值作代表);
的值以及该公司这300个工作日每日汽车销售量的平均数(同一组中的数据用该组区间的中点值作代表);
(2)以频率估计概率,若在所有工作日中随机选择4天,记汽车销售量在区间 内的天数为
内的天数为 ,求
,求 的分布列及数学期望;
的分布列及数学期望;
(3)为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:抽奖区有 两个盒子,其中
两个盒子,其中 盒中放有9张金卡、1张银卡,
盒中放有9张金卡、1张银卡, 盒中放有2张金卡、8张银卡,顾客在不知情的情况下随机选择其中一个盒子进行抽奖,直到抽到金卡则抽奖结束(每次抽出一张卡,然后放回原来的盒中,再进行下次抽奖,中途可更换盒子),卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率相同,求小明在首次抽奖抽出银卡的条件下,第二次从另外一个盒子中抽奖抽出金卡的概率.
盒中放有2张金卡、8张银卡,顾客在不知情的情况下随机选择其中一个盒子进行抽奖,直到抽到金卡则抽奖结束(每次抽出一张卡,然后放回原来的盒中,再进行下次抽奖,中途可更换盒子),卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率相同,求小明在首次抽奖抽出银卡的条件下,第二次从另外一个盒子中抽奖抽出金卡的概率.
 的值以及该公司这300个工作日每日汽车销售量的平均数(同一组中的数据用该组区间的中点值作代表);
的值以及该公司这300个工作日每日汽车销售量的平均数(同一组中的数据用该组区间的中点值作代表);(2)以频率估计概率,若在所有工作日中随机选择4天,记汽车销售量在区间
 内的天数为
内的天数为 ,求
,求 的分布列及数学期望;
的分布列及数学期望;(3)为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:抽奖区有
 两个盒子,其中
两个盒子,其中 盒中放有9张金卡、1张银卡,
盒中放有9张金卡、1张银卡, 盒中放有2张金卡、8张银卡,顾客在不知情的情况下随机选择其中一个盒子进行抽奖,直到抽到金卡则抽奖结束(每次抽出一张卡,然后放回原来的盒中,再进行下次抽奖,中途可更换盒子),卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率相同,求小明在首次抽奖抽出银卡的条件下,第二次从另外一个盒子中抽奖抽出金卡的概率.
盒中放有2张金卡、8张银卡,顾客在不知情的情况下随机选择其中一个盒子进行抽奖,直到抽到金卡则抽奖结束(每次抽出一张卡,然后放回原来的盒中,再进行下次抽奖,中途可更换盒子),卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率相同,求小明在首次抽奖抽出银卡的条件下,第二次从另外一个盒子中抽奖抽出金卡的概率.
您最近一年使用:0次
2024-08-06更新
|
338次组卷
|
2卷引用:黑龙江省大庆外国语学校2025届高三上学期第一次教学质量检测数学试卷
名校
4 . 现有一批疫苗试剂,拟进入动物试验阶段,将对一组动物(共10只)进行试验.第一轮注射,对该组的每只动物都注射一次,若检验出该组中有9只或10只动物产生抗体,说明疫苗有效,试验终止;否则对没有产生抗体的动物进行第二轮注射,再次检验.如果被二次注射的动物都产生抗体,说明疫苗有效,否则需要改进疫苗.设每只动物是否产生抗体相互独立,两次注射疫苗互不影响,且产生抗体的概率均为 .若试验只需一轮注射的概率为
.若试验只需一轮注射的概率为 ,需要注射第二轮的概率为
,需要注射第二轮的概率为 ,且该组中某一只动物在这次试验中只被注射一次的概率为
,且该组中某一只动物在这次试验中只被注射一次的概率为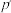 (
( 均用含
均用含 的多项式表示),再设该组动物总共需要注射的次数
的多项式表示),再设该组动物总共需要注射的次数 的数学期望为
的数学期望为 ,则( )
,则( )
 .若试验只需一轮注射的概率为
.若试验只需一轮注射的概率为 ,需要注射第二轮的概率为
,需要注射第二轮的概率为 ,且该组中某一只动物在这次试验中只被注射一次的概率为
,且该组中某一只动物在这次试验中只被注射一次的概率为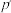 (
( 均用含
均用含 的多项式表示),再设该组动物总共需要注射的次数
的多项式表示),再设该组动物总共需要注射的次数 的数学期望为
的数学期望为 ,则( )
,则( )A. | B. |
C. | D. |
您最近一年使用:0次
名校
解题方法
5 . 已知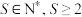 ,在平面直角坐标系
,在平面直角坐标系 中有一个点阵,点阵中所有点的集合为
中有一个点阵,点阵中所有点的集合为 ,从集全
,从集全 中任取两个不同的点,用随机变量
中任取两个不同的点,用随机变量 表示它们之间的距离.
表示它们之间的距离.
(1)当 时,求
时,求 的分布列及期望.
的分布列及期望.
(2)对给定的正整数 .
.
(ⅰ)求随机变量 的所有可能取值的个数(用含有
的所有可能取值的个数(用含有 的式子表示);
的式子表示);
(ⅱ)求概率 (用含有
(用含有 的式子表示).
的式子表示).
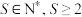 ,在平面直角坐标系
,在平面直角坐标系 中有一个点阵,点阵中所有点的集合为
中有一个点阵,点阵中所有点的集合为 ,从集全
,从集全 中任取两个不同的点,用随机变量
中任取两个不同的点,用随机变量 表示它们之间的距离.
表示它们之间的距离.(1)当
 时,求
时,求 的分布列及期望.
的分布列及期望.(2)对给定的正整数
 .
.(ⅰ)求随机变量
 的所有可能取值的个数(用含有
的所有可能取值的个数(用含有 的式子表示);
的式子表示);(ⅱ)求概率
 (用含有
(用含有 的式子表示).
的式子表示).
您最近一年使用:0次
名校
解题方法
6 . 短视频已成为当下宣传的重要手段,东北某著名景点利用短视频宣传增加旅游热度,为调查某天南北方游客来此景点旅游是否与收看短视频有关,该景点对当天前来旅游的500名游客调查得知,南方游客有300人,因收看短视频而来的280名游客中南方游客有200人.
(1)依据调查数据完成如下列联表,根据小概率值 的独立性检验,分析南北方游客来此景点旅游是否与收看短视颍有关联:单位:人
的独立性检验,分析南北方游客来此景点旅游是否与收看短视颍有关联:单位:人
(2)为了增加游客的旅游乐趣,该景点设置一款5人传球游戏,每个人得到球后都等可能地传给其余4人之一,现有甲、乙等5人参加此游戏,球首先由甲传出.
(i)求经过 次传递后球回到甲的概率;
次传递后球回到甲的概率;
(ii)记前 次传递中球传到乙的次数为
次传递中球传到乙的次数为 ,求
,求 的数学期望.
的数学期望.
参考公式: ,其中
,其中 ;
;
附表:
(1)依据调查数据完成如下列联表,根据小概率值
 的独立性检验,分析南北方游客来此景点旅游是否与收看短视颍有关联:单位:人
的独立性检验,分析南北方游客来此景点旅游是否与收看短视颍有关联:单位:人| 游客 | 短视频 | 合计 | |
| 收看 | 未看 | ||
| 南方游客 | |||
| 北方游客 | |||
| 合计 | |||
(i)求经过
 次传递后球回到甲的概率;
次传递后球回到甲的概率;(ii)记前
 次传递中球传到乙的次数为
次传递中球传到乙的次数为 ,求
,求 的数学期望.
的数学期望.参考公式:
 ,其中
,其中 ;
;
附表:
 | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-04-13更新
|
2328次组卷
|
6卷引用:黑龙江省大庆市萨尔图区大庆实验中学2023-2024学年高二下学期期末考试数学试题
黑龙江省大庆市萨尔图区大庆实验中学2023-2024学年高二下学期期末考试数学试题吉林省吉林地区普通高中2024届高三第三次模拟考试数学试题(已下线)8.3.1分类变量与列联表+8.3.2独立性检验 第三练 能力提升拔高(已下线)数学(新高考卷02,新题型结构)湖南省长沙市第一中学2023-2024学年高二下学期期末考试数学试题(已下线)专题6 回归分析与独立性检验复杂问题【讲】(高二期末压轴专项)
名校
7 . 某校开展科普知识团队接力闯关活动,该活动共有两关,每个团队由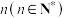 位成员组成,成员按预先安排的顺序依次上场,具体规则如下:若某成员第一关闯关成功,则该成员继续闯第二关,否则该成员结束闯关并由下一位成员接力去闯第一关;若某成员第二关闯关成功,则该团队接力闯关活动结束,否则该成员结束闯关并由下一位成员接力去闯第二关;当第二关闯关成功或所有成员全部上场参加了闯关,该团队接力闯关活动结束.
位成员组成,成员按预先安排的顺序依次上场,具体规则如下:若某成员第一关闯关成功,则该成员继续闯第二关,否则该成员结束闯关并由下一位成员接力去闯第一关;若某成员第二关闯关成功,则该团队接力闯关活动结束,否则该成员结束闯关并由下一位成员接力去闯第二关;当第二关闯关成功或所有成员全部上场参加了闯关,该团队接力闯关活动结束.
已知A团队每位成员闯过第一关和第二关的概率均为 ,且每位成员闯关是否成功互不影响,每关结果也互不影响.
,且每位成员闯关是否成功互不影响,每关结果也互不影响.
(1)用随机变量X表示A团队第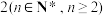 位成员的闯关数,求X的分布列;
位成员的闯关数,求X的分布列;
(2)已知A团队第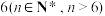 位成员上场并闯过第二关,求恰好是第3位成员闯过第一关的概率;
位成员上场并闯过第二关,求恰好是第3位成员闯过第一关的概率;
(3)记随机变量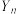 表示A团队第
表示A团队第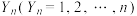 位成员上场并结束闯关活动,证明
位成员上场并结束闯关活动,证明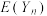 单调递增,并求使
单调递增,并求使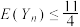 的n的最大值.
的n的最大值.
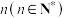 位成员组成,成员按预先安排的顺序依次上场,具体规则如下:若某成员第一关闯关成功,则该成员继续闯第二关,否则该成员结束闯关并由下一位成员接力去闯第一关;若某成员第二关闯关成功,则该团队接力闯关活动结束,否则该成员结束闯关并由下一位成员接力去闯第二关;当第二关闯关成功或所有成员全部上场参加了闯关,该团队接力闯关活动结束.
位成员组成,成员按预先安排的顺序依次上场,具体规则如下:若某成员第一关闯关成功,则该成员继续闯第二关,否则该成员结束闯关并由下一位成员接力去闯第一关;若某成员第二关闯关成功,则该团队接力闯关活动结束,否则该成员结束闯关并由下一位成员接力去闯第二关;当第二关闯关成功或所有成员全部上场参加了闯关,该团队接力闯关活动结束.已知A团队每位成员闯过第一关和第二关的概率均为
 ,且每位成员闯关是否成功互不影响,每关结果也互不影响.
,且每位成员闯关是否成功互不影响,每关结果也互不影响.(1)用随机变量X表示A团队第
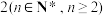 位成员的闯关数,求X的分布列;
位成员的闯关数,求X的分布列;(2)已知A团队第
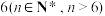 位成员上场并闯过第二关,求恰好是第3位成员闯过第一关的概率;
位成员上场并闯过第二关,求恰好是第3位成员闯过第一关的概率;(3)记随机变量
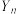 表示A团队第
表示A团队第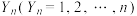 位成员上场并结束闯关活动,证明
位成员上场并结束闯关活动,证明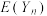 单调递增,并求使
单调递增,并求使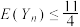 的n的最大值.
的n的最大值.
您最近一年使用:0次
2024-04-10更新
|
808次组卷
|
3卷引用:黑龙江省大庆市实验中学实验二部2023-2024学年高三下学期得分训练数学试题(四)
黑龙江省大庆市实验中学实验二部2023-2024学年高三下学期得分训练数学试题(四)湖南省长沙市第一中学2023-2024学年高二下学期第一次阶段性检测数学试题(已下线)第三章 随机变量及其分布列 专题一 随机变量的期望 微点3 随机变量的分布列、期望综合训练【培优版】
解题方法
8 . 某企业对500个产品逐一进行检验,检验“合格”方能出厂.产品检验需要进行三项工序A、B、C,三项检验全部通过则被确定为“合格”,若其中至少2项检验不通过的产品确定为“不合格”,有且只有1项检验不通过的产品将其进行改良后再检验A、B两项工序,如果这两项全部通过则被确定为“合格”,否则确定为“不合格”.每个产品检验A、B、C三项工序工作相互独立,每一项检验不通过的概率均为p( ).
).
(1)记某产品被确定为“不合格”的概率为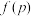 ,求
,求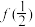 的值;
的值;
(2)若不需要重新检验的每个产品的检验费用为120元,需要重新检验的每个产品两次检验费用为200元.除检验费用外,其他费用为2万元,且这500个产品全部检验,该企业预算检验总费用(包含检验费用与其他费用)为10万元.试预测该企业检验总费用是否会超过预算?并说明理由.
 ).
).(1)记某产品被确定为“不合格”的概率为
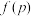 ,求
,求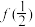 的值;
的值;(2)若不需要重新检验的每个产品的检验费用为120元,需要重新检验的每个产品两次检验费用为200元.除检验费用外,其他费用为2万元,且这500个产品全部检验,该企业预算检验总费用(包含检验费用与其他费用)为10万元.试预测该企业检验总费用是否会超过预算?并说明理由.
您最近一年使用:0次
2024-02-13更新
|
600次组卷
|
3卷引用:黑龙江省大庆市水利学校(职普融通部)2025届高三第一次模拟考试数学试题(暨复读班开学摸底考试)
名校
解题方法
9 . 某人在 次射击中击中目标的次数为
次射击中击中目标的次数为 ,
,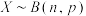 ,其中
,其中 ,
, ,击中奇数次为事件
,击中奇数次为事件 ,则( )
,则( )
 次射击中击中目标的次数为
次射击中击中目标的次数为 ,
,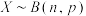 ,其中
,其中 ,
, ,击中奇数次为事件
,击中奇数次为事件 ,则( )
,则( )A.若 , ,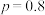 ,则 ,则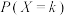 取最大值时 取最大值时 |
B.当 时, 时, 取得最小值 取得最小值 |
C.当 时, 时,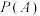 随着 随着 的增大而增大 的增大而增大 |
D.当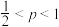 时, 时,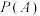 随着 随着 的增大而减小 的增大而减小 |
您最近一年使用:0次
2024-06-01更新
|
514次组卷
|
22卷引用:黑龙江省牡丹江市第一高级中学2023-2024学年高二下学期5月期中考试数学试题
黑龙江省牡丹江市第一高级中学2023-2024学年高二下学期5月期中考试数学试题山东省泰安肥城市2023届高考适应性训练数学试题(三)山东省新高考质量检测联盟2024届高三第一次质量检测数学试题(A)(已下线)模块一 专题2 概率(北师大2019版)(已下线)模块一 专题4 随机变量及其分布 (人教A)(已下线)模块一 专题3 概率 (苏教版)(已下线)第四篇 概率与统计 专题7 常见分布 微点3 常见分布综合训练(已下线)单元提升卷11 统计与概率湖北省武昌实验中学2023-2024学年高三上学期10月月考数学试题(已下线)考点13 二项分布与超级几何分布 2024届高考数学考点总动员【练】(已下线)第11讲 二项分布与超几何分布-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)随机变量及其分布(已下线)专题04 超几何分布+二项分布+正态分布压轴题(4)(已下线)7.4.1 二项分布(分层练习,6大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)黄金卷02(已下线)专题7.10 随机变量及其分布全章综合测试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题10.1 概率与统计的综合运用【十一大题型】(举一反三)(新高考专用)-1辽宁省大连市第八中学2023-2024学年高二下学期4月月考数学试题(已下线)第七章:随机变量及其分布章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)高二下期末考前押题卷02--高二期末考点大串讲(人教B版2019选择性必修)(已下线)概率、随机变量及其分布-综合测试卷A卷(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点4 概率分布模型拓展【培优版】
名校
10 . 中华人民共和国第十九届亚运会将于2023年9月在杭州举办.为了组建一支朝气蓬勃、训练有素的赛会志愿者队伍,向全国人民奉献一场精彩圆满的体育盛会,组委会欲从6名男志愿者,4名女志愿者中随机抽取3人聘为志愿者队的队长.下列说法正确的是( )
A.设事件A:“抽取的3人中至少有一名男志愿者”,事件B:“抽取的3人中全是男志愿者”,则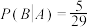 |
B.设事件C:“抽取的3人中既有男志愿者,也有女志愿者”,则 |
C.用 表示抽取的3人中女志愿者的人数,则 表示抽取的3人中女志愿者的人数,则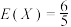 |
D.用 表示抽取的3人中男志愿者的人数,则 表示抽取的3人中男志愿者的人数,则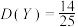 |
您最近一年使用:0次
2023-07-05更新
|
1260次组卷
|
8卷引用:黑龙江省牡丹江市第三高级中学2023-2024学年高三上学期第一次月考数学试题
黑龙江省牡丹江市第三高级中学2023-2024学年高三上学期第一次月考数学试题河南省许昌市2022-2023学年高二下学期期末数学试题(已下线)模块二 专题3 计数原理、随机变量及其分布列 B提升卷(人教A)(已下线)第四篇 概率与统计 专题7 常见分布 微点1 常见分布(已下线)专题04 超几何分布+二项分布+正态分布压轴题(4)(已下线)高二下学期期中复习选择题压轴题十五大题型专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)高二下学期期末数学试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)【巩固卷】第3章 概率素养检测 单元测试A-湘教版(2019)选择性必修第二册



