解题方法
1 . 现有一种不断分裂的 细胞,每个时间周期
细胞,每个时间周期 内分裂一次,一个
内分裂一次,一个 细胞每次分裂能生成一个或两个新的
细胞每次分裂能生成一个或两个新的 细胞,每次分裂后原
细胞,每次分裂后原 细胞消失.设每次分裂成一个新
细胞消失.设每次分裂成一个新 细胞的概率为
细胞的概率为 ,分裂成两个新
,分裂成两个新 细胞的概率为
细胞的概率为 ;新细胞在下一个周期
;新细胞在下一个周期 内可以继续分裂,每个细胞间相互独立.设有一个初始的
内可以继续分裂,每个细胞间相互独立.设有一个初始的 细胞,在第一个周期
细胞,在第一个周期 中开始分裂,其中
中开始分裂,其中 .
.
(1)设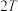 结束后,
结束后, 细胞的数量为
细胞的数量为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)设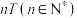 结束后,
结束后, 细胞数量为
细胞数量为 的概率为
的概率为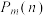 .
.
(ⅰ)求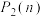 ;
;
(ⅱ)证明: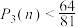 .
.
 细胞,每个时间周期
细胞,每个时间周期 内分裂一次,一个
内分裂一次,一个 细胞每次分裂能生成一个或两个新的
细胞每次分裂能生成一个或两个新的 细胞,每次分裂后原
细胞,每次分裂后原 细胞消失.设每次分裂成一个新
细胞消失.设每次分裂成一个新 细胞的概率为
细胞的概率为 ,分裂成两个新
,分裂成两个新 细胞的概率为
细胞的概率为 ;新细胞在下一个周期
;新细胞在下一个周期 内可以继续分裂,每个细胞间相互独立.设有一个初始的
内可以继续分裂,每个细胞间相互独立.设有一个初始的 细胞,在第一个周期
细胞,在第一个周期 中开始分裂,其中
中开始分裂,其中 .
.(1)设
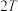 结束后,
结束后, 细胞的数量为
细胞的数量为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)设
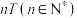 结束后,
结束后, 细胞数量为
细胞数量为 的概率为
的概率为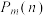 .
.(ⅰ)求
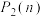 ;
;(ⅱ)证明:
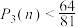 .
.
您最近一年使用:0次
名校
2 . 某汽车销售公司为了提升公司的业绩,现将最近300个工作日每日的汽车销售情况进行统计,如图所示. 的值以及该公司这300个工作日每日汽车销售量的平均数(同一组中的数据用该组区间的中点值作代表);
的值以及该公司这300个工作日每日汽车销售量的平均数(同一组中的数据用该组区间的中点值作代表);
(2)以频率估计概率,若在所有工作日中随机选择4天,记汽车销售量在区间 内的天数为
内的天数为 ,求
,求 的分布列及数学期望;
的分布列及数学期望;
(3)为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:抽奖区有 两个盒子,其中
两个盒子,其中 盒中放有9张金卡、1张银卡,
盒中放有9张金卡、1张银卡, 盒中放有2张金卡、8张银卡,顾客在不知情的情况下随机选择其中一个盒子进行抽奖,直到抽到金卡则抽奖结束(每次抽出一张卡,然后放回原来的盒中,再进行下次抽奖,中途可更换盒子),卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率相同,求小明在首次抽奖抽出银卡的条件下,第二次从另外一个盒子中抽奖抽出金卡的概率.
盒中放有2张金卡、8张银卡,顾客在不知情的情况下随机选择其中一个盒子进行抽奖,直到抽到金卡则抽奖结束(每次抽出一张卡,然后放回原来的盒中,再进行下次抽奖,中途可更换盒子),卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率相同,求小明在首次抽奖抽出银卡的条件下,第二次从另外一个盒子中抽奖抽出金卡的概率.
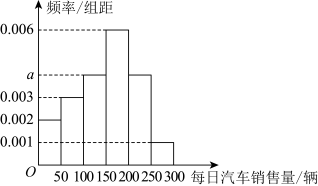
 的值以及该公司这300个工作日每日汽车销售量的平均数(同一组中的数据用该组区间的中点值作代表);
的值以及该公司这300个工作日每日汽车销售量的平均数(同一组中的数据用该组区间的中点值作代表);(2)以频率估计概率,若在所有工作日中随机选择4天,记汽车销售量在区间
 内的天数为
内的天数为 ,求
,求 的分布列及数学期望;
的分布列及数学期望;(3)为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:抽奖区有
 两个盒子,其中
两个盒子,其中 盒中放有9张金卡、1张银卡,
盒中放有9张金卡、1张银卡, 盒中放有2张金卡、8张银卡,顾客在不知情的情况下随机选择其中一个盒子进行抽奖,直到抽到金卡则抽奖结束(每次抽出一张卡,然后放回原来的盒中,再进行下次抽奖,中途可更换盒子),卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率相同,求小明在首次抽奖抽出银卡的条件下,第二次从另外一个盒子中抽奖抽出金卡的概率.
盒中放有2张金卡、8张银卡,顾客在不知情的情况下随机选择其中一个盒子进行抽奖,直到抽到金卡则抽奖结束(每次抽出一张卡,然后放回原来的盒中,再进行下次抽奖,中途可更换盒子),卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率相同,求小明在首次抽奖抽出银卡的条件下,第二次从另外一个盒子中抽奖抽出金卡的概率.
您最近一年使用:0次
2024-08-06更新
|
338次组卷
|
2卷引用:河南省驻马店部分学校2024年普通高等学校招生全国统一考试模拟数学试题(二)
名校
解题方法
3 . 在11分制乒乓球比赛中,每赢一球得1分,当某局打成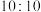 平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为p,乙发球时甲得分的概率为
平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为p,乙发球时甲得分的概率为 ,各球的结果相互独立.已知在某局双方
,各球的结果相互独立.已知在某局双方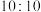 平后,甲先发球,两人又打了X个球该局比赛结束,且
平后,甲先发球,两人又打了X个球该局比赛结束,且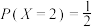 .
.
(1)求p的值;
(2)求再打2个球甲新增的得分Y的分布列和均值;
(3)记事件“ ,
, 且甲获胜”的概率为
且甲获胜”的概率为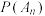 ,求
,求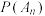 .
.
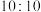 平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为p,乙发球时甲得分的概率为
平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为p,乙发球时甲得分的概率为 ,各球的结果相互独立.已知在某局双方
,各球的结果相互独立.已知在某局双方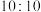 平后,甲先发球,两人又打了X个球该局比赛结束,且
平后,甲先发球,两人又打了X个球该局比赛结束,且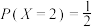 .
.(1)求p的值;
(2)求再打2个球甲新增的得分Y的分布列和均值;
(3)记事件“
 ,
, 且甲获胜”的概率为
且甲获胜”的概率为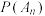 ,求
,求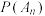 .
.
您最近一年使用:0次
2024-07-17更新
|
259次组卷
|
2卷引用:河南省开封市2023-2024学年高二下学期7月期末数学试题
名校
4 . 甲袋中有2个红球、3个黄球,乙袋中有3个红球、2个黄球,同时从甲、乙两袋中取出2个球交换,分别记交换后甲、乙两个袋子中红球个数的数学期望为 、
、 ,方差为
,方差为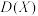 、
、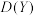 ,则下列结论正确的是( )
,则下列结论正确的是( )
 、
、 ,方差为
,方差为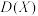 、
、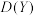 ,则下列结论正确的是( )
,则下列结论正确的是( )A.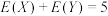 | B.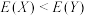 |
C.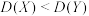 | D. |
您最近一年使用:0次
2024-07-13更新
|
224次组卷
|
2卷引用:河南省郑州市宇华实验学校2023-2024学年高二下学期7月期末考试数学试题
5 . 已知函数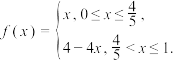 随机变量
随机变量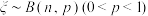 ,随机变量
,随机变量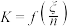 ,
, 的期望为
的期望为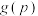 .
.
(1)当 时,求
时,求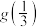 ;
;
(2)当 时,求
时,求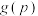 的表达式.
的表达式.
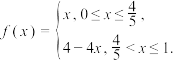 随机变量
随机变量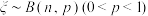 ,随机变量
,随机变量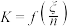 ,
, 的期望为
的期望为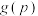 .
.(1)当
 时,求
时,求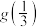 ;
;(2)当
 时,求
时,求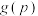 的表达式.
的表达式.
您最近一年使用:0次
2024-06-16更新
|
436次组卷
|
4卷引用:河南省部分重点高中2023-2024学年高三下学期5月联考数学试卷 (新高考)
河南省部分重点高中2023-2024学年高三下学期5月联考数学试卷 (新高考)(已下线)辽宁省沈阳市第二中学2024届高三下学期三模数学试题内蒙古自治区锡林郭勒盟2024届高三下学期5月模拟考试理科数学试题(已下线)概率、随机变量及其分布-综合测试卷B卷
名校
解题方法
6 . 切比雪夫不等式是19世纪俄国数学家切比雪夫(1821.5~1894.12)在研究统计规律时发现的,其内容是:对于任一随机变量 ,若其数学期望
,若其数学期望 和方差
和方差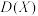 均存在,则对任意正实数
均存在,则对任意正实数 ,有
,有 .根据该不等式可以对事件
.根据该不等式可以对事件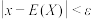 的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号
的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号 次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量
次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量 ,为了至少有
,为了至少有 的把握使发射信号“1”的频率在区间
的把握使发射信号“1”的频率在区间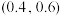 内,估计信号发射次数
内,估计信号发射次数 的值至少为
的值至少为______ .
 ,若其数学期望
,若其数学期望 和方差
和方差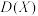 均存在,则对任意正实数
均存在,则对任意正实数 ,有
,有 .根据该不等式可以对事件
.根据该不等式可以对事件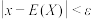 的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号
的概率作出估计.在数字通信中,信号是由数字“0”和“1”组成的序列,现连续发射信号 次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量
次,每次发射信号“0”和“1”是等可能的.记发射信号“1”的次数为随机变量 ,为了至少有
,为了至少有 的把握使发射信号“1”的频率在区间
的把握使发射信号“1”的频率在区间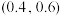 内,估计信号发射次数
内,估计信号发射次数 的值至少为
的值至少为
您最近一年使用:0次
2024-06-11更新
|
937次组卷
|
13卷引用:河南省驻马店市新蔡县第一高级中学2025届高三上学期8月开学考试数学试题
河南省驻马店市新蔡县第一高级中学2025届高三上学期8月开学考试数学试题辽宁省沈阳市第二中学2024届高三第五次模拟考试数学试题(已下线)第3套 期末全真模拟卷(高二期末基础卷)(已下线)高二数学下学期期末押题卷01-2023-2024学年高二数学同步讲与练(人教A版2019)山东省部分学校2023-2024学年高二下学期期末联合教学质量检测数学试卷山东省泰安市部分学校2023-2024学年高二下学期期末测试数学试题山东省齐鲁名师联盟2025届高三上学期第一次诊断考试数学试题宁夏回族自治区银川一中2025届高三上学期八月开学复习巩固测试数学试题(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点4 概率分布模型拓展【培优版】(已下线)重难点突破03 高等背景下概率论新定义(七大题型)(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点1 概率统计与数列交汇(一)【基础版】(已下线)第五章 概率统计创新问题 专题七 概率统计中的新定义问题 微点4 概率统计中的新定义问题(四)【培优版】(已下线)第五章 概率统计创新问题 专题三 概率统计中的函数思想 微点2 概率统计中的函数思想(二)【培优版】
名校
7 . 设集合 为
为 的非空子集,随机变量X,Y分别表示取到子集
的非空子集,随机变量X,Y分别表示取到子集 中的最大元素和最小元素的数值.
中的最大元素和最小元素的数值.
(1)若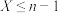 的概率为
的概率为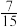 ,求
,求 ;
;
(2)若 ,求
,求 且
且 的概率;
的概率;
(3)求随机变量 的均值
的均值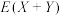 .
.
 为
为 的非空子集,随机变量X,Y分别表示取到子集
的非空子集,随机变量X,Y分别表示取到子集 中的最大元素和最小元素的数值.
中的最大元素和最小元素的数值.(1)若
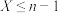 的概率为
的概率为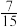 ,求
,求 ;
;(2)若
 ,求
,求 且
且 的概率;
的概率;(3)求随机变量
 的均值
的均值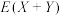 .
.
您最近一年使用:0次
2024-06-09更新
|
328次组卷
|
3卷引用:河南省信阳市新县高级中学2024届高三数学考前仿真冲刺卷
8 . 甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选一张,并比较所选卡片上数字的大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛后,甲的总得分不小于2的概率为_________ .
您最近一年使用:0次
2024-06-07更新
|
22075次组卷
|
14卷引用:河南省部分中学2023-2024学年高二下学期联考数学试题
河南省部分中学2023-2024学年高二下学期联考数学试题2024年新课标全国Ⅰ卷数学真题(已下线)2024年高考数学真题完全解读(新高考Ⅰ卷)专题10计数原理、概率、随机变量及其分布(已下线)2024年新课标全国Ⅰ卷数学真题变式题11-15(已下线)五年新高考专题08计数原理与概率统计(已下线)三年新高考专题08计数原理与概率统计(已下线)第2套 期末全真模拟卷(高二期末中等)(已下线)专题11 概率(4大考向真题解读)海南省儋州市第三中学2023-2024学年高二下学期数学期末复习考试试题(2)江西省南昌市聚仁高级中学2025届高三上学期八月月考数学试题山东省淄博市淄博实验中学2024-2025学年高三上学期10月月考数学试题(已下线)第05讲 古典概型与概率的基本性质(八大题型)(练习)(已下线)第07讲 离散型随机变量及其分布列、数字特征(六大题型)(讲义)-2
名校
9 . 第二次世界大战期间,了解德军坦克的生产能力对盟军具有非常重要的战略意义.已知德军的每辆坦克上都有一个按生产顺序从1开始的连续编号.假设德军某月生产的坦克总数为N,随机缴获该月生产的n辆( )坦克的编号为
)坦克的编号为 ,
, ,…,
,…, ,记
,记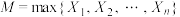 ,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
甲同学根据样本均值估计总体均值的思想,用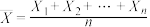 估计总体的均值,因此
估计总体的均值,因此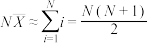 ,得
,得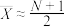 ,故可用
,故可用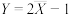 作为N的估计.
作为N的估计.
乙同学对此提出异议,认为这种方法可能出现 的无意义结果.例如,当
的无意义结果.例如,当 ,
, 时,若
时,若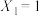 ,
,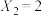 ,
,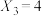 ,则
,则 ,此时
,此时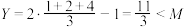 .
.
(1)当 ,
, 时,求条件概率
时,求条件概率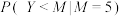 ;
;
(2)为了避免甲同学方法的缺点,乙同学提出直接用M作为N的估计值.当 ,
, 时,求随机变量M的分布列和均值
时,求随机变量M的分布列和均值 ;
;
(3)丙同学认为估计值的均值应稳定于实际值,但直观上可以发现 与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断
与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断 与N的大小关系,并给出证明.
与N的大小关系,并给出证明.
 )坦克的编号为
)坦克的编号为 ,
, ,…,
,…, ,记
,记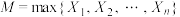 ,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.甲同学根据样本均值估计总体均值的思想,用
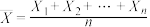 估计总体的均值,因此
估计总体的均值,因此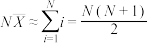 ,得
,得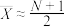 ,故可用
,故可用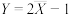 作为N的估计.
作为N的估计.乙同学对此提出异议,认为这种方法可能出现
 的无意义结果.例如,当
的无意义结果.例如,当 ,
, 时,若
时,若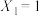 ,
,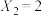 ,
,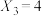 ,则
,则 ,此时
,此时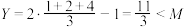 .
.(1)当
 ,
, 时,求条件概率
时,求条件概率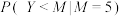 ;
;(2)为了避免甲同学方法的缺点,乙同学提出直接用M作为N的估计值.当
 ,
, 时,求随机变量M的分布列和均值
时,求随机变量M的分布列和均值 ;
;(3)丙同学认为估计值的均值应稳定于实际值,但直观上可以发现
 与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断
与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断 与N的大小关系,并给出证明.
与N的大小关系,并给出证明.
您最近一年使用:0次
2024-05-28更新
|
1145次组卷
|
4卷引用:河南省南阳市社旗县第一高级中学2024届高三下学期三模理科数学试题
名校
10 . 学校食堂每天中午都会提供 两种套餐供学生选择(学生只能选择其中的一种),经过统计分析发现:学生第一天选择
两种套餐供学生选择(学生只能选择其中的一种),经过统计分析发现:学生第一天选择 套餐概率为
套餐概率为 ,选择
,选择 套餐概率为
套餐概率为 ;而前一天选择了
;而前一天选择了 套餐的学生第二天选择
套餐的学生第二天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率为
套餐的概率为 ;前一天选择
;前一天选择 套餐的学生第二天选择
套餐的学生第二天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率也是
套餐的概率也是 ;如此反复,记某同学第
;如此反复,记某同学第 天选择
天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率为
套餐的概率为 ;5个月(150天)后,记甲、乙、丙三位同学选择
;5个月(150天)后,记甲、乙、丙三位同学选择 套餐的人数为
套餐的人数为 ,则下列说法中
,则下列说法中正确 的是( )
 两种套餐供学生选择(学生只能选择其中的一种),经过统计分析发现:学生第一天选择
两种套餐供学生选择(学生只能选择其中的一种),经过统计分析发现:学生第一天选择 套餐概率为
套餐概率为 ,选择
,选择 套餐概率为
套餐概率为 ;而前一天选择了
;而前一天选择了 套餐的学生第二天选择
套餐的学生第二天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率为
套餐的概率为 ;前一天选择
;前一天选择 套餐的学生第二天选择
套餐的学生第二天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率也是
套餐的概率也是 ;如此反复,记某同学第
;如此反复,记某同学第 天选择
天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率为
套餐的概率为 ;5个月(150天)后,记甲、乙、丙三位同学选择
;5个月(150天)后,记甲、乙、丙三位同学选择 套餐的人数为
套餐的人数为 ,则下列说法中
,则下列说法中A.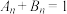 | B.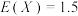 | C.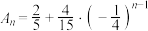 | D.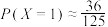 |
您最近一年使用:0次
2024-05-24更新
|
819次组卷
|
8卷引用:河南省驻马店市新蔡县第一高级中学2023-2024学年高二下学期6月月考数学试题
河南省驻马店市新蔡县第一高级中学2023-2024学年高二下学期6月月考数学试题广东省四会中学、广信中学2023-2024学年高二下学期第二次联考数学试题(已下线)【江苏专用】高二下学期期末模拟测试B卷(已下线)【讲】 专题三 复杂背景的概率计算问题(压轴大全)山东省烟台市牟平区第一中学2023-2024学年高二下学期6月限时练(月考)数学试题(已下线)第1套 期末全真模拟卷(高二期末较难卷)(已下线)第2套 期末全真模拟卷(高二期末较难)(已下线)第三章 随机变量及其分布列 专题一 随机变量的期望 微点1 随机变量的分布列、期望(一)【培优版】



