名校
1 . 二项分布是离散型随机变量重要的概率模型.我们已经知道,若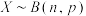 ,则
,则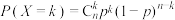 .多项分布是二项分布的推广,同样是重复
.多项分布是二项分布的推广,同样是重复 次试验,不同的是每次试验的结果不止2种,而有
次试验,不同的是每次试验的结果不止2种,而有 种,记这
种,记这 种结果为事件
种结果为事件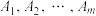 ,它们的概率分别为
,它们的概率分别为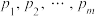 ,则
,则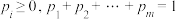 .现考虑某厂生产的产品分成一等品
.现考虑某厂生产的产品分成一等品 、二等品
、二等品 、三等品
、三等品 和不合格品
和不合格品 ,它们出现的概率分别为
,它们出现的概率分别为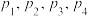 ,从该厂产品中抽出
,从该厂产品中抽出 个,研究各类产品出现的次数的情况,就是一个多项分布.由于产品很多,每次抽取可以看作是独立重复的.
个,研究各类产品出现的次数的情况,就是一个多项分布.由于产品很多,每次抽取可以看作是独立重复的.
(1)若从该厂产品中抽出4个,且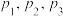 和
和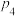 分别为
分别为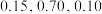 和0.05,求抽出一等品1个、二等品2个,三等品1个的概率;
和0.05,求抽出一等品1个、二等品2个,三等品1个的概率;
(2)现从该厂中抽出 个产品,记事件
个产品,记事件 出现的次数为随机变量
出现的次数为随机变量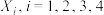 .为了定出这一多项分布的分布列,只需求出事件
.为了定出这一多项分布的分布列,只需求出事件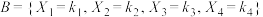 的概率,其中
的概率,其中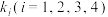 为非负整数,
为非负整数,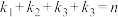 .
.
(i)求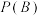 ;
;
(ii)对于上述多项分布,求在给定 的条件下,随机变量
的条件下,随机变量 的数学期望.
的数学期望.
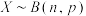 ,则
,则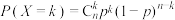 .多项分布是二项分布的推广,同样是重复
.多项分布是二项分布的推广,同样是重复 次试验,不同的是每次试验的结果不止2种,而有
次试验,不同的是每次试验的结果不止2种,而有 种,记这
种,记这 种结果为事件
种结果为事件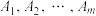 ,它们的概率分别为
,它们的概率分别为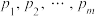 ,则
,则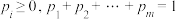 .现考虑某厂生产的产品分成一等品
.现考虑某厂生产的产品分成一等品 、二等品
、二等品 、三等品
、三等品 和不合格品
和不合格品 ,它们出现的概率分别为
,它们出现的概率分别为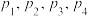 ,从该厂产品中抽出
,从该厂产品中抽出 个,研究各类产品出现的次数的情况,就是一个多项分布.由于产品很多,每次抽取可以看作是独立重复的.
个,研究各类产品出现的次数的情况,就是一个多项分布.由于产品很多,每次抽取可以看作是独立重复的.(1)若从该厂产品中抽出4个,且
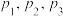 和
和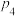 分别为
分别为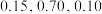 和0.05,求抽出一等品1个、二等品2个,三等品1个的概率;
和0.05,求抽出一等品1个、二等品2个,三等品1个的概率;(2)现从该厂中抽出
 个产品,记事件
个产品,记事件 出现的次数为随机变量
出现的次数为随机变量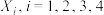 .为了定出这一多项分布的分布列,只需求出事件
.为了定出这一多项分布的分布列,只需求出事件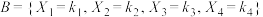 的概率,其中
的概率,其中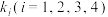 为非负整数,
为非负整数,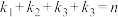 .
.(i)求
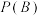 ;
;(ii)对于上述多项分布,求在给定
 的条件下,随机变量
的条件下,随机变量 的数学期望.
的数学期望.
您最近一年使用:0次
名校
解题方法
2 . 高考数学试题第二部分为多选题,共3个小题,每小题有4个选项,其中有2个或3个是正确选项,全部选对得6分,部分选对得部分分,有选错的得0分.若正确答案是2个选项,只选对1个得3分,有选错的得0分;若正确答案是3个选项,只选对1个得2分,只选对2个得4分,有选错的得0分.小明对其中的一道题完全不会,该题有两个正确选项的概率是 ,记
,记 为小明随机选择1个选项的得分,记
为小明随机选择1个选项的得分,记 为小明随机选择2个选项的得分,则( )
为小明随机选择2个选项的得分,则( )
 ,记
,记 为小明随机选择1个选项的得分,记
为小明随机选择1个选项的得分,记 为小明随机选择2个选项的得分,则( )
为小明随机选择2个选项的得分,则( )A. | B. |
C. | D. |
您最近一年使用:0次
3 . 某学校的数学节活动中,其中有一项“抽幸运数字”擂台游戏,分甲乙双方,游戏开始时,甲方有2张互不相同的牌,乙方有3张互不相同的牌,其中的2张牌与甲方的牌相同,剩下一张为“幸运数字牌”.游戏规则为:
①双方交替从对方抽取一张牌,甲方先从乙方中抽取;
②若抽到对方的牌与自己的某张牌一致,则将这两张牌丢弃;
③最后剩一张牌(幸运数字牌)时,持有幸运数字牌的那方获胜.
假设每一次从对方抽到任一张牌的概率都相同.奖励规则为:若甲方胜可获得200积分,乙方胜可获得100积分.
(1)已知某一轮游戏中,记 为甲乙两方抽牌次数之和.
为甲乙两方抽牌次数之和.
(ⅰ)求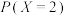 ;
;
(ⅱ)求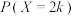 ,
,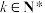 ;
;
(2)为使获得积分的期望最大,你会选择哪一方进行游戏?并说明理由.
①双方交替从对方抽取一张牌,甲方先从乙方中抽取;
②若抽到对方的牌与自己的某张牌一致,则将这两张牌丢弃;
③最后剩一张牌(幸运数字牌)时,持有幸运数字牌的那方获胜.
假设每一次从对方抽到任一张牌的概率都相同.奖励规则为:若甲方胜可获得200积分,乙方胜可获得100积分.
(1)已知某一轮游戏中,记
 为甲乙两方抽牌次数之和.
为甲乙两方抽牌次数之和.(ⅰ)求
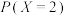 ;
;(ⅱ)求
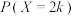 ,
,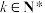 ;
;(2)为使获得积分的期望最大,你会选择哪一方进行游戏?并说明理由.
您最近一年使用:0次
4 . 某观影平台为了解观众对最近上映的某部影片的评价情况(评价结果仅有“好评”、“差评”),从平台所有参与评价的观众中随机抽取216人进行调查,部分数据如下表所示(单位:人):
(1)判断是否有 的把握认为“对该部影片的评价与性别有关”?
的把握认为“对该部影片的评价与性别有关”?
(2)若将频率视为概率,从观影平台的所有给出“好评”的观众中随机抽取3人,用随机变量 表示被抽到的男性观众的人数,求
表示被抽到的男性观众的人数,求 的分布列;
的分布列;
(3)在抽出的216人中,从给出“好评”的观众中利用分层抽样的方法抽取10人,从给出“差评”的观众中抽取 人.现从这
人.现从这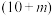 人中,随机抽出2人,用随机变量
人中,随机抽出2人,用随机变量 表示被抽到的给出“好评”的女性观众的人数.若随机变量
表示被抽到的给出“好评”的女性观众的人数.若随机变量 的数学期望不小于1,求
的数学期望不小于1,求 的最大值.
的最大值.
参考公式: ,其中
,其中 .
.
参考数据:
好评 | 差评 | 合计 | |
男性 | 40 | 68 | 108 |
女性 | 60 | 48 | 108 |
合计 | 100 | 116 | 216 |
 的把握认为“对该部影片的评价与性别有关”?
的把握认为“对该部影片的评价与性别有关”?(2)若将频率视为概率,从观影平台的所有给出“好评”的观众中随机抽取3人,用随机变量
 表示被抽到的男性观众的人数,求
表示被抽到的男性观众的人数,求 的分布列;
的分布列;(3)在抽出的216人中,从给出“好评”的观众中利用分层抽样的方法抽取10人,从给出“差评”的观众中抽取
 人.现从这
人.现从这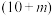 人中,随机抽出2人,用随机变量
人中,随机抽出2人,用随机变量 表示被抽到的给出“好评”的女性观众的人数.若随机变量
表示被抽到的给出“好评”的女性观众的人数.若随机变量 的数学期望不小于1,求
的数学期望不小于1,求 的最大值.
的最大值.参考公式:
 ,其中
,其中 .
.参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
名校
解题方法
5 . 盒中有标记数字 的小球各1个.
的小球各1个.
(1)随机一次取出3个小球,求3个小球上的数字之和大于10的概率;
(2)随机一次取出1个小球并记录下小球上的数字,重复以上操作,直到记录下的数字中同时出现1和2或者同时出现3和4.记操作的次数为 .
.
(i)若每次操作后不将取出的小球放回盒中,求 的分布列及数学期望
的分布列及数学期望 ;
;
(ii)若每次操作后将取出的小球放回盒中,求 的数学期望
的数学期望 .
.
 的小球各1个.
的小球各1个.(1)随机一次取出3个小球,求3个小球上的数字之和大于10的概率;
(2)随机一次取出1个小球并记录下小球上的数字,重复以上操作,直到记录下的数字中同时出现1和2或者同时出现3和4.记操作的次数为
 .
.(i)若每次操作后不将取出的小球放回盒中,求
 的分布列及数学期望
的分布列及数学期望 ;
;(ii)若每次操作后将取出的小球放回盒中,求
 的数学期望
的数学期望 .
.
您最近一年使用:0次
名校
6 . 第二次世界大战期间,了解德军坦克的生产能力对盟军具有非常重要的战略意义.已知德军的每辆坦克上都有一个按生产顺序从1开始的连续编号.假设德军某月生产的坦克总数为N,随机缴获该月生产的n辆( )坦克的编号为
)坦克的编号为 ,
, ,…,
,…, ,记
,记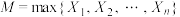 ,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
甲同学根据样本均值估计总体均值的思想,用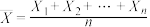 估计总体的均值,因此
估计总体的均值,因此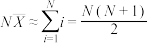 ,得
,得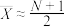 ,故可用
,故可用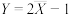 作为N的估计.
作为N的估计.
乙同学对此提出异议,认为这种方法可能出现 的无意义结果.例如,当
的无意义结果.例如,当 ,
, 时,若
时,若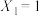 ,
,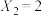 ,
,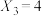 ,则
,则 ,此时
,此时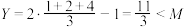 .
.
(1)当 ,
, 时,求条件概率
时,求条件概率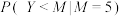 ;
;
(2)为了避免甲同学方法的缺点,乙同学提出直接用M作为N的估计值.当 ,
, 时,求随机变量M的分布列和均值
时,求随机变量M的分布列和均值 ;
;
(3)丙同学认为估计值的均值应稳定于实际值,但直观上可以发现 与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断
与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断 与N的大小关系,并给出证明.
与N的大小关系,并给出证明.
 )坦克的编号为
)坦克的编号为 ,
, ,…,
,…, ,记
,记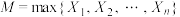 ,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.
,即缴获坦克中的最大编号.现考虑用概率统计的方法利用缴获的坦克编号信息估计总数N.甲同学根据样本均值估计总体均值的思想,用
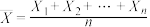 估计总体的均值,因此
估计总体的均值,因此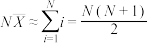 ,得
,得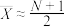 ,故可用
,故可用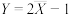 作为N的估计.
作为N的估计.乙同学对此提出异议,认为这种方法可能出现
 的无意义结果.例如,当
的无意义结果.例如,当 ,
, 时,若
时,若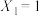 ,
,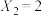 ,
,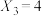 ,则
,则 ,此时
,此时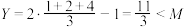 .
.(1)当
 ,
, 时,求条件概率
时,求条件概率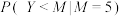 ;
;(2)为了避免甲同学方法的缺点,乙同学提出直接用M作为N的估计值.当
 ,
, 时,求随机变量M的分布列和均值
时,求随机变量M的分布列和均值 ;
;(3)丙同学认为估计值的均值应稳定于实际值,但直观上可以发现
 与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断
与N存在明确的大小关系,因此乙同学的方法也存在缺陷.请判断 与N的大小关系,并给出证明.
与N的大小关系,并给出证明.
您最近一年使用:0次
2024-05-28更新
|
1145次组卷
|
4卷引用:浙江省(杭州二中、绍兴一中、温州中学、金华一中、衢州二中)五校联考2024届高考数学模拟卷
7 . 在坐标平面内  的区域,随机生成一个横纵坐标均为整数的一个整点
的区域,随机生成一个横纵坐标均为整数的一个整点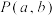
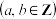 ,记该点到坐标原点的距离是随机变量X
,记该点到坐标原点的距离是随机变量X
相关公式: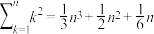
(1)当 时,写出X的分布列和期望.
时,写出X的分布列和期望.
(2)记随机变量 与
与 分别表示
分别表示 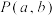 的横纵坐标.
的横纵坐标.
①求出 的期望
的期望 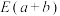
②现在实际上选取了四个点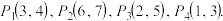 尝试运用样本的平均值去估计数学期望,以此来得到估计值
尝试运用样本的平均值去估计数学期望,以此来得到估计值  (四舍五入取整).
(四舍五入取整).
(3)记方差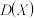 ,试证明
,试证明 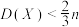 .
.
 的区域,随机生成一个横纵坐标均为整数的一个整点
的区域,随机生成一个横纵坐标均为整数的一个整点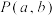
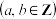 ,记该点到坐标原点的距离是随机变量X
,记该点到坐标原点的距离是随机变量X相关公式:
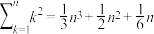
(1)当
 时,写出X的分布列和期望.
时,写出X的分布列和期望.(2)记随机变量
 与
与 分别表示
分别表示 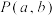 的横纵坐标.
的横纵坐标.①求出
 的期望
的期望 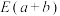
②现在实际上选取了四个点
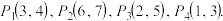 尝试运用样本的平均值去估计数学期望,以此来得到估计值
尝试运用样本的平均值去估计数学期望,以此来得到估计值  (四舍五入取整).
(四舍五入取整).(3)记方差
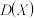 ,试证明
,试证明 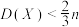 .
.
您最近一年使用:0次
名校
解题方法
8 . 某大学有甲、乙两个运动场.假设同学们可以任意选择其中一个运动场锻炼,也可选择不锻炼,一天最多锻炼一次,一次只能选择一个运动场.若同学们每次锻炼选择去甲或乙运动场的概率均为 ,每次选择相互独立.设王同学在某个假期的三天内去运动场锻炼的次数为
,每次选择相互独立.设王同学在某个假期的三天内去运动场锻炼的次数为 ,已知
,已知 的分布列如下:(其中
的分布列如下:(其中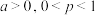 )
)
(1)记事件 表示王同学假期三天内去运动场锻炼
表示王同学假期三天内去运动场锻炼 次
次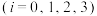 ,事件
,事件 表示王同学在这三天内去甲运动场锻炼的次数大于去乙运动场锻炼的次数.当
表示王同学在这三天内去甲运动场锻炼的次数大于去乙运动场锻炼的次数.当 时,试根据全概率公式求
时,试根据全概率公式求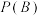 的值;
的值;
(2)是否存在实数 ,使得
,使得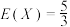 ?若存在,求
?若存在,求 的值:若不存在,请说明理由;
的值:若不存在,请说明理由;
(3)记 表示事件“甲运动场举办锻炼有奖的抽奖活动”,
表示事件“甲运动场举办锻炼有奖的抽奖活动”, 表示事件“王同学去甲运动场锻炼”,
表示事件“王同学去甲运动场锻炼”,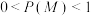 .已知王同学在甲运动场举办锻炼有奖的抽奖活动的情况下去甲运动场锻炼的概率,比不举办抽奖活动的情况下去甲运动场锻炼的概率大,证明:
.已知王同学在甲运动场举办锻炼有奖的抽奖活动的情况下去甲运动场锻炼的概率,比不举办抽奖活动的情况下去甲运动场锻炼的概率大,证明: .
.
 ,每次选择相互独立.设王同学在某个假期的三天内去运动场锻炼的次数为
,每次选择相互独立.设王同学在某个假期的三天内去运动场锻炼的次数为 ,已知
,已知 的分布列如下:(其中
的分布列如下:(其中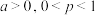 )
) | 0 | 1 | 2 | 3 |
 | 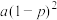 | 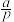 |  |  |
 表示王同学假期三天内去运动场锻炼
表示王同学假期三天内去运动场锻炼 次
次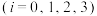 ,事件
,事件 表示王同学在这三天内去甲运动场锻炼的次数大于去乙运动场锻炼的次数.当
表示王同学在这三天内去甲运动场锻炼的次数大于去乙运动场锻炼的次数.当 时,试根据全概率公式求
时,试根据全概率公式求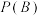 的值;
的值;(2)是否存在实数
 ,使得
,使得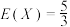 ?若存在,求
?若存在,求 的值:若不存在,请说明理由;
的值:若不存在,请说明理由;(3)记
 表示事件“甲运动场举办锻炼有奖的抽奖活动”,
表示事件“甲运动场举办锻炼有奖的抽奖活动”, 表示事件“王同学去甲运动场锻炼”,
表示事件“王同学去甲运动场锻炼”,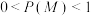 .已知王同学在甲运动场举办锻炼有奖的抽奖活动的情况下去甲运动场锻炼的概率,比不举办抽奖活动的情况下去甲运动场锻炼的概率大,证明:
.已知王同学在甲运动场举办锻炼有奖的抽奖活动的情况下去甲运动场锻炼的概率,比不举办抽奖活动的情况下去甲运动场锻炼的概率大,证明: .
.
您最近一年使用:0次
2024-05-04更新
|
1523次组卷
|
3卷引用:浙江省温州市平阳县万全综合高级中学2023-2024学年中职高二下学期期末普高数学试题
浙江省温州市平阳县万全综合高级中学2023-2024学年中职高二下学期期末普高数学试题湖南师范大学附属中学2024届高三下学期模拟(二)数学试卷(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)
名校
9 . 甲口袋中装有2个黑球和1个白球,乙口袋中装有1个黑球和2个白球.设从甲、乙两个口袋中各任取一个球交换放入另一个口袋为一次操作,经过 次这样的操作,记甲口袋中黑球个数为
次这样的操作,记甲口袋中黑球个数为 .
.
(1)写出 的分布列并计算
的分布列并计算 ;
;
(2)某人重复进行了100次操作,记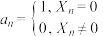 ,
, ,求该数列
,求该数列 的前100项和
的前100项和 的最大值;
的最大值;
(3)定性分析当交换次数趋向于无穷时,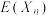 趋向的值.
趋向的值.
 次这样的操作,记甲口袋中黑球个数为
次这样的操作,记甲口袋中黑球个数为 .
.(1)写出
 的分布列并计算
的分布列并计算 ;
;(2)某人重复进行了100次操作,记
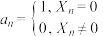 ,
, ,求该数列
,求该数列 的前100项和
的前100项和 的最大值;
的最大值;(3)定性分析当交换次数趋向于无穷时,
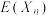 趋向的值.
趋向的值.
您最近一年使用:0次
名校
10 . 甲、乙两人进行知识问答比赛,共有 道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为
道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为 和
和 ,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.
,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.
(1)若 ,
, ,求甲获胜的概率;
,求甲获胜的概率;
(2)若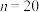 ,设甲第
,设甲第 题的得分为随机变量
题的得分为随机变量 ,一次比赛中得到
,一次比赛中得到 的一组观测值
的一组观测值 ,如下表.现利用统计方法来估计
,如下表.现利用统计方法来估计 的值:
的值:
①设随机变量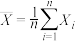 ,若以观测值
,若以观测值 的均值
的均值 作为
作为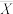 的数学期望,请以此求出
的数学期望,请以此求出 的估计值
的估计值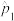 ;
;
②设随机变量 取到观测值
取到观测值 的概率为
的概率为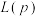 ,即
,即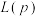
 ;在一次抽样中获得这一组特殊观测值的概率应该最大,随着
;在一次抽样中获得这一组特殊观测值的概率应该最大,随着 的变化,用使得
的变化,用使得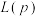 达到最大时
达到最大时 的取值
的取值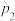 作为参数
作为参数 的一个估计值.求
的一个估计值.求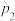 .
.
表1:甲得分的一组观测值.
附:若随机变量 ,
, 的期望
的期望 ,
, 都存在,则
都存在,则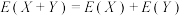 .
.
 道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为
道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的概率分别为 和
和 ,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.
,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,未抢到题得0分,最后累计总分多的人获胜.(1)若
 ,
, ,求甲获胜的概率;
,求甲获胜的概率;(2)若
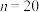 ,设甲第
,设甲第 题的得分为随机变量
题的得分为随机变量 ,一次比赛中得到
,一次比赛中得到 的一组观测值
的一组观测值 ,如下表.现利用统计方法来估计
,如下表.现利用统计方法来估计 的值:
的值:①设随机变量
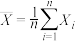 ,若以观测值
,若以观测值 的均值
的均值 作为
作为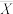 的数学期望,请以此求出
的数学期望,请以此求出 的估计值
的估计值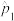 ;
;②设随机变量
 取到观测值
取到观测值 的概率为
的概率为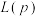 ,即
,即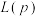
 ;在一次抽样中获得这一组特殊观测值的概率应该最大,随着
;在一次抽样中获得这一组特殊观测值的概率应该最大,随着 的变化,用使得
的变化,用使得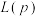 达到最大时
达到最大时 的取值
的取值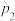 作为参数
作为参数 的一个估计值.求
的一个估计值.求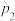 .
.| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分 | 1 | 0 | 0 | ﹣1 | 1 | 1 | ﹣1 | 0 | 0 | 0 |
| 题目 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 得分 | ﹣1 | 0 | 1 | 1 | ﹣1 | 0 | 0 | 0 | 1 | 0 |
附:若随机变量
 ,
, 的期望
的期望 ,
, 都存在,则
都存在,则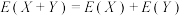 .
.
您最近一年使用:0次
2024-04-19更新
|
3135次组卷
|
9卷引用:浙江省天域全国名校协作体2023-2024学年高三二模数学试题
浙江省天域全国名校协作体2023-2024学年高三二模数学试题山东省青岛第二中学2024届高三下学期二模考试数学试题(已下线)数学(江苏专用02)河北省重点高中2024届高三下学期5月模拟考试数学试题(一)(已下线)模块4 二模重组卷 第6套 全真模拟卷江苏省苏州实验中学2023-2024学年高二下学期5月月考数学试题广东省广州市执信中学2024届高三下学期教学情况检测(三)数学试题(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)(已下线)第三章 随机变量及其分布列 专题一 随机变量的期望 微点3 随机变量的分布列、期望综合训练【培优版】