1 . 已知三个正整数的和为8,用 表示这三个数中最小的数,则
表示这三个数中最小的数,则 的期望
的期望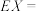
__________ .
 表示这三个数中最小的数,则
表示这三个数中最小的数,则 的期望
的期望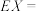
您最近一年使用:0次
2024-07-22更新
|
405次组卷
|
2卷引用:江西省抚州市多所学校2025届高三下学期第一次大联考数学试题
名校
2 . 小郅和小豪同学玩纸牌游戏,小郅面前有标有点数分别为1、2、3、4、5的纸牌各1张,小豪面前有标号为1、2、3、4、5的纸牌分别有5、4、3、2、1张(抽牌阶段抽到每张牌的概率均等),规定首先小豪同学从其面前纸堆中抽取一张牌点数记为 ,然后放回牌堆,随后小郅同学任意从其面前牌堆中抽取
,然后放回牌堆,随后小郅同学任意从其面前牌堆中抽取 张牌,记这
张牌,记这 张纸牌的点数和为
张纸牌的点数和为 ,则
,则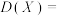
__________ ,
__________ .
 ,然后放回牌堆,随后小郅同学任意从其面前牌堆中抽取
,然后放回牌堆,随后小郅同学任意从其面前牌堆中抽取 张牌,记这
张牌,记这 张纸牌的点数和为
张纸牌的点数和为 ,则
,则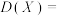

您最近一年使用:0次
名校
3 . 南昌二中一直有个优秀的传统“毕业学习经验分享会”:每届高考结束后,各班推荐优秀学生代表与下一届学生进行学习经验分享.2024届高三年级班号依次为0,1,2,…,27,高三0班推荐2名男生和2名女生,其余各班均推荐1名男生和1名女生参加分享会;第一场分享会的4名学生嘉宾是从高三0班的优秀学生代表中选出的2名和高三1班的2名优秀学生代表共同形成,第二场分享会的4名学生嘉宾是从上一场4名嘉宾中选出的2名和高三2班的2名优秀学生代表共同形成,…,按照这样的方式,依次进行到第二十七场分享会.
(1)求在第一场分享会学生嘉宾中有2名男生的概率;
(2)求在第二场分享会学生嘉宾中有2名男生的概率;
(3)记在第二十七场分享会学生嘉宾中男生人数为 ,求
,求 的分布列和期望.
的分布列和期望.
(1)求在第一场分享会学生嘉宾中有2名男生的概率;
(2)求在第二场分享会学生嘉宾中有2名男生的概率;
(3)记在第二十七场分享会学生嘉宾中男生人数为
 ,求
,求 的分布列和期望.
的分布列和期望.
您最近一年使用:0次
4 . 设集合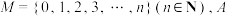 为
为 的非空子集,随机变量
的非空子集,随机变量 分别表示取到
分别表示取到 中的最小元素和最大元素的数值.
中的最小元素和最大元素的数值.
(1)若 ,求事件“
,求事件“ 且
且 ”的概率;
”的概率;
(2)若 的概率为
的概率为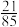 ,求
,求 ;
;
(3)求随机变量 的均值
的均值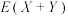 .
.
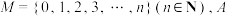 为
为 的非空子集,随机变量
的非空子集,随机变量 分别表示取到
分别表示取到 中的最小元素和最大元素的数值.
中的最小元素和最大元素的数值.(1)若
 ,求事件“
,求事件“ 且
且 ”的概率;
”的概率;(2)若
 的概率为
的概率为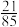 ,求
,求 ;
;(3)求随机变量
 的均值
的均值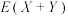 .
.
您最近一年使用:0次
5 . 甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选一张,并比较所选卡片上数字的大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛后,甲的总得分不小于2的概率为_________ .
您最近一年使用:0次
2024-06-07更新
|
22070次组卷
|
14卷引用:江西省南昌市聚仁高级中学2025届高三上学期八月月考数学试题
江西省南昌市聚仁高级中学2025届高三上学期八月月考数学试题2024年新课标全国Ⅰ卷数学真题(已下线)2024年高考数学真题完全解读(新高考Ⅰ卷)专题10计数原理、概率、随机变量及其分布(已下线)2024年新课标全国Ⅰ卷数学真题变式题11-15(已下线)五年新高考专题08计数原理与概率统计(已下线)三年新高考专题08计数原理与概率统计(已下线)第2套 期末全真模拟卷(高二期末中等)河南省部分中学2023-2024学年高二下学期联考数学试题(已下线)专题11 概率(4大考向真题解读)海南省儋州市第三中学2023-2024学年高二下学期数学期末复习考试试题(2)山东省淄博市淄博实验中学2024-2025学年高三上学期10月月考数学试题(已下线)第05讲 古典概型与概率的基本性质(八大题型)(练习)(已下线)第07讲 离散型随机变量及其分布列、数字特征(六大题型)(讲义)-2
名校
解题方法
6 . 在三维空间中,立方体的坐标可用三维坐标 表示,其中
表示,其中 ,而在
,而在 维空间中
维空间中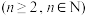 ,以单位长度为边长的“立方体”的顶点坐标可表示为
,以单位长度为边长的“立方体”的顶点坐标可表示为 维坐标
维坐标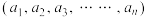 ,其中
,其中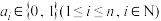 .现有如下定义:在
.现有如下定义:在 维空间中两点间的曼哈顿距离为两点
维空间中两点间的曼哈顿距离为两点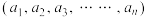 与
与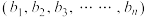 坐标差的绝对值之和,即为
坐标差的绝对值之和,即为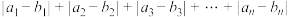 .回答下列问题:
.回答下列问题:
(1)求出 维“立方体”的顶点数;
维“立方体”的顶点数;
(2)在 维“立方体”中任取两个不同顶点,记随机变量
维“立方体”中任取两个不同顶点,记随机变量 为所取两点间的曼哈顿距离.
为所取两点间的曼哈顿距离.
①求 的分布列与期望;
的分布列与期望;
②求 的方差.
的方差.
 表示,其中
表示,其中 ,而在
,而在 维空间中
维空间中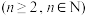 ,以单位长度为边长的“立方体”的顶点坐标可表示为
,以单位长度为边长的“立方体”的顶点坐标可表示为 维坐标
维坐标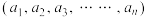 ,其中
,其中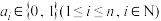 .现有如下定义:在
.现有如下定义:在 维空间中两点间的曼哈顿距离为两点
维空间中两点间的曼哈顿距离为两点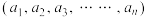 与
与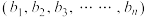 坐标差的绝对值之和,即为
坐标差的绝对值之和,即为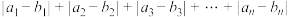 .回答下列问题:
.回答下列问题:(1)求出
 维“立方体”的顶点数;
维“立方体”的顶点数;(2)在
 维“立方体”中任取两个不同顶点,记随机变量
维“立方体”中任取两个不同顶点,记随机变量 为所取两点间的曼哈顿距离.
为所取两点间的曼哈顿距离.①求
 的分布列与期望;
的分布列与期望;②求
 的方差.
的方差.
您最近一年使用:0次
2024-05-15更新
|
1519次组卷
|
7卷引用:江西省新八校2024届高三第二次联考数学试题
江西省新八校2024届高三第二次联考数学试题广东省深圳外国语学校2023-2024学年高二下学期第二次月考数学试题湖北省武昌实验中学2024届高三下学期5月高考适应性考试数学试卷(已下线)专题7 以新定义为背景的相关问题【练】(高二期末压轴专项)湖北省襄阳市第五中学2025届高三8月月考数学试卷(已下线)专题6 概率与统计中的新定义压轴大题(一)【讲】广东省广州市天河中学2024-2025学年高三上学期综合模拟测试(一)数学试卷
名校
7 . 甲进行摸球跳格游戏.图上标有第1格,第2格, ,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第
,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第 格的概率为
格的概率为 .
.
(1)甲在一次摸球中摸出红球的个数记为 ,求
,求 的分布列和期望;
的分布列和期望;
(2)证明:数列 为等比数列,并求
为等比数列,并求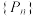 的通项公式.
的通项公式.
 ,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第
,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第 格的概率为
格的概率为 .
.(1)甲在一次摸球中摸出红球的个数记为
 ,求
,求 的分布列和期望;
的分布列和期望;(2)证明:数列
 为等比数列,并求
为等比数列,并求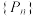 的通项公式.
的通项公式.
您最近一年使用:0次
2024-04-19更新
|
912次组卷
|
2卷引用:江西省抚州市临川第一中学2023-2024学年高二下学期6月检测二数学试题
名校
8 . 从1,2,3, ,
, 这
这 个数中随机抽一个数记为
个数中随机抽一个数记为 ,再从1,2,
,再从1,2, ,
, 中随机抽一个数记为
中随机抽一个数记为 ,则
,则
______ .
 ,
, 这
这 个数中随机抽一个数记为
个数中随机抽一个数记为 ,再从1,2,
,再从1,2, ,
, 中随机抽一个数记为
中随机抽一个数记为 ,则
,则
您最近一年使用:0次
2024·全国·模拟预测
名校
解题方法
9 . 已知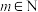 ,
, ,
, ,
, ,
, ,
,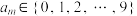 ,记
,记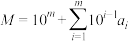 .当
.当 ,
, ,
, ,
,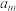 ,中含
,中含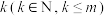 个6时,所有
个6时,所有 不同值的个数记为
不同值的个数记为 .下列说法正确的有( )
.下列说法正确的有( )
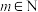 ,
, ,
, ,
, ,
, ,
,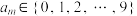 ,记
,记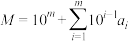 .当
.当 ,
, ,
, ,
,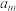 ,中含
,中含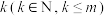 个6时,所有
个6时,所有 不同值的个数记为
不同值的个数记为 .下列说法正确的有( )
.下列说法正确的有( )A.若 ,则 ,则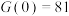 |
B.若 ,则 ,则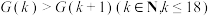 |
C.对于任意奇数 |
D.对于任意整数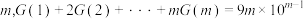 |
您最近一年使用:0次
2024-01-14更新
|
895次组卷
|
6卷引用:江西省上饶市私立新知学校2023-2024学年高二上学期期末数学试题
江西省上饶市私立新知学校2023-2024学年高二上学期期末数学试题(已下线)2024南通名师高考原创卷(十)吉林省长春市第二实验中学2023-2024学年高二下学期开学测试数学试题(已下线)专题01 两个计数原理与排列组合(7类压轴题型)-【常考压轴题】2023-2024学年高二数学压轴题攻略(人教A版2019选择性必修第三册)(已下线)压轴题08计数原理、二项式定理、概率统计压轴题6题型汇总(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点5 重要的概率分布模型综合训练【培优版】
名校
解题方法
10 . 某游戏游玩规则如下:每次游戏有机会获得5分,10分或20分的积分,且每次游戏只能获得一种积分;每次游戏获得5分,10分,20分的概率分别为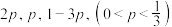 ,三次游戏为一轮,一轮游戏结束后,计算本轮游戏总积分.
,三次游戏为一轮,一轮游戏结束后,计算本轮游戏总积分.
(1)求某人在一轮游戏中,累计积分不超过25分的概率(用含 的代数式表示);
的代数式表示);
(2)当某人在一轮游戏中累计积分在区间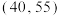 内的概率取得最大值时,求一轮游戏累计积分的数学期望.
内的概率取得最大值时,求一轮游戏累计积分的数学期望.
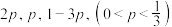 ,三次游戏为一轮,一轮游戏结束后,计算本轮游戏总积分.
,三次游戏为一轮,一轮游戏结束后,计算本轮游戏总积分.(1)求某人在一轮游戏中,累计积分不超过25分的概率(用含
 的代数式表示);
的代数式表示);(2)当某人在一轮游戏中累计积分在区间
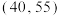 内的概率取得最大值时,求一轮游戏累计积分的数学期望.
内的概率取得最大值时,求一轮游戏累计积分的数学期望.
您最近一年使用:0次
2024-01-10更新
|
1314次组卷
|
5卷引用:江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(五)
江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(五)新疆维吾尔自治区慕华·优策2023-2024学年高三上学期第一次联考数学试题四川省宜宾市第六中学校2024届高三上学期期末数学(理)试题(已下线)专题04 超几何分布+二项分布+正态分布压轴题(1)(已下线)题型27 5类概率统计大题综合解题技巧



