1 . 羽毛球比赛采用21分制,比赛规则如下:一场比赛为三局两胜制,在一局比赛中,每赢一球得1分,先得21分且至少领先2分者获胜,该局比赛结束;当比分打成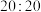 后,以投掷硬币的方式选择发球权,随后得分者拥有发球权,一方领先2分者获胜,该局比赛结束.现有甲、乙两人进行一场21分制的羽毛球比赛,假设甲发球时甲得分的概率为
后,以投掷硬币的方式选择发球权,随后得分者拥有发球权,一方领先2分者获胜,该局比赛结束.现有甲、乙两人进行一场21分制的羽毛球比赛,假设甲发球时甲得分的概率为 ,乙发球时甲得分的概率为
,乙发球时甲得分的概率为 ,各球的比赛结果相互独立,且各局的比赛结果也相互独立.已知第一局目前比分为
,各球的比赛结果相互独立,且各局的比赛结果也相互独立.已知第一局目前比分为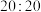 .
.
(1)若再打两个球,这两个球甲得分为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)假设一旦两人比分相等,以投掷硬币的方式选择发球权,求一局比赛甲获胜的概率 ;
;
(3)用 估计每局比赛甲获胜的概率,求该场比赛甲获胜的概率.
估计每局比赛甲获胜的概率,求该场比赛甲获胜的概率.
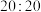 后,以投掷硬币的方式选择发球权,随后得分者拥有发球权,一方领先2分者获胜,该局比赛结束.现有甲、乙两人进行一场21分制的羽毛球比赛,假设甲发球时甲得分的概率为
后,以投掷硬币的方式选择发球权,随后得分者拥有发球权,一方领先2分者获胜,该局比赛结束.现有甲、乙两人进行一场21分制的羽毛球比赛,假设甲发球时甲得分的概率为 ,乙发球时甲得分的概率为
,乙发球时甲得分的概率为 ,各球的比赛结果相互独立,且各局的比赛结果也相互独立.已知第一局目前比分为
,各球的比赛结果相互独立,且各局的比赛结果也相互独立.已知第一局目前比分为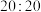 .
.(1)若再打两个球,这两个球甲得分为
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)假设一旦两人比分相等,以投掷硬币的方式选择发球权,求一局比赛甲获胜的概率
 ;
;(3)用
 估计每局比赛甲获胜的概率,求该场比赛甲获胜的概率.
估计每局比赛甲获胜的概率,求该场比赛甲获胜的概率.
您最近一年使用:0次
2024-09-09更新
|
398次组卷
|
2卷引用:云南省2025届高三上学期9月名校联考数学卷
名校
解题方法
2 . 设集合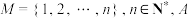 为
为 的非空子集,随机变量
的非空子集,随机变量 分别表示取到子集
分别表示取到子集 中元素的最大值和最小值.
中元素的最大值和最小值.
(1)若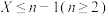 的概率为
的概率为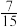 ,求
,求 ;
;
(2)若 ,求
,求 且
且 的概率;
的概率;
(3)已知:对于随机变量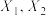 ,有
,有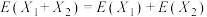 .求随机变量
.求随机变量 的期望
的期望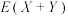 .
.
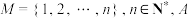 为
为 的非空子集,随机变量
的非空子集,随机变量 分别表示取到子集
分别表示取到子集 中元素的最大值和最小值.
中元素的最大值和最小值.(1)若
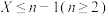 的概率为
的概率为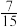 ,求
,求 ;
;(2)若
 ,求
,求 且
且 的概率;
的概率;(3)已知:对于随机变量
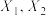 ,有
,有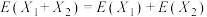 .求随机变量
.求随机变量 的期望
的期望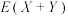 .
.
您最近一年使用:0次
名校
解题方法
3 . 现有标号依次为1,2,…,n的n个盒子,标号为1号的盒子里有2个红球和2个白球,其余盒子里都是1个红球和1个白球.现从1号盒子里取出2个球放入2号盒子,再从2号盒子里取出2个球放入3号盒子,…,依次进行到从 号盒子里取出2个球放入n号盒子为止.
号盒子里取出2个球放入n号盒子为止.
(1)当 时,求2号盒子里有2个红球的概率;
时,求2号盒子里有2个红球的概率;
(2)当 时,求3号盒子里的红球的个数
时,求3号盒子里的红球的个数 的分布列;
的分布列;
(3)记n号盒子中红球的个数为 ,求
,求 的期望
的期望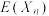 .
.
 号盒子里取出2个球放入n号盒子为止.
号盒子里取出2个球放入n号盒子为止.(1)当
 时,求2号盒子里有2个红球的概率;
时,求2号盒子里有2个红球的概率;(2)当
 时,求3号盒子里的红球的个数
时,求3号盒子里的红球的个数 的分布列;
的分布列;(3)记n号盒子中红球的个数为
 ,求
,求 的期望
的期望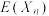 .
.
您最近一年使用:0次
2024-02-04更新
|
4380次组卷
|
12卷引用:云南三校2024届高三高考备考实用性联考卷(七)数学试卷
云南三校2024届高三高考备考实用性联考卷(七)数学试卷浙江省温州市2024届高三上学期期末考试数学试题(已下线)第三套 复盘卷(已下线)新题型01 新高考新结构二十一大考点汇总-3(已下线)第七章 概率初步(续)(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)山东省烟台市招远市2023-2024学年高二下学期4月月考数学试题单元测试A卷——第七章 随机变量及其分布湖南名校联考联合体2023-2024学年高二下学期第二次(期中)联考试卷(已下线)离散型随机变量及其分布列、数字特征-一轮复习考点专练辽宁省沈阳市东北育才学校2024-2025学年高三上学期第一次模拟考试暨假期质量测试数学试卷(已下线)第三章 随机变量及其分布列 专题四 随机变量分布列、期望、方差的应用 微点4 概率分布在生活、生产实践中的应用(四)【培优版】
名校
解题方法
4 . 国学小组有编号为1,2,3,…, 的
的 位同学,现在有两个选择题,每人答对第一题的概率为
位同学,现在有两个选择题,每人答对第一题的概率为 、答对第二题的概率为
、答对第二题的概率为 ,每个同学的答题过程都是相互独立的,比赛规则如下:①按编号由小到大的顺序依次进行,第1号同学开始第1轮出赛,先答第一题;②若第
,每个同学的答题过程都是相互独立的,比赛规则如下:①按编号由小到大的顺序依次进行,第1号同学开始第1轮出赛,先答第一题;②若第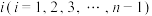 号同学未答对第一题,则第
号同学未答对第一题,则第 轮比赛失败,由第
轮比赛失败,由第 号同学继继续比赛;③若第
号同学继继续比赛;③若第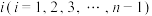 号同学答对第一题,则再答第二题,若该生答对第二题,则比赛在第
号同学答对第一题,则再答第二题,若该生答对第二题,则比赛在第 轮结束;若该生未答对第二题,则第
轮结束;若该生未答对第二题,则第 轮比赛失败,由第
轮比赛失败,由第 号同学继续答第二题,且以后比赛的同学不答第一题;④若比赛进行到了第
号同学继续答第二题,且以后比赛的同学不答第一题;④若比赛进行到了第 轮,则不管第
轮,则不管第 号同学答题情况,比赛结束.
号同学答题情况,比赛结束.
(1)令随机变量 表示
表示 名同学在第
名同学在第 轮比赛结束,当
轮比赛结束,当 时,求随机变量
时,求随机变量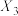 的分布列;
的分布列;
(2)若把比赛规则③改为:若第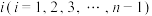 号同学未答对第二题,则第
号同学未答对第二题,则第 轮比赛失败,第
轮比赛失败,第 号同学重新从第一题开始作答.令随机变量
号同学重新从第一题开始作答.令随机变量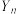 表示
表示 名挑战者在第
名挑战者在第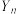 轮比赛结束.
轮比赛结束.
①求随机变量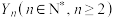 的分布列;
的分布列;
②证明: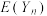 单调递增,且小于3.
单调递增,且小于3.
 的
的 位同学,现在有两个选择题,每人答对第一题的概率为
位同学,现在有两个选择题,每人答对第一题的概率为 、答对第二题的概率为
、答对第二题的概率为 ,每个同学的答题过程都是相互独立的,比赛规则如下:①按编号由小到大的顺序依次进行,第1号同学开始第1轮出赛,先答第一题;②若第
,每个同学的答题过程都是相互独立的,比赛规则如下:①按编号由小到大的顺序依次进行,第1号同学开始第1轮出赛,先答第一题;②若第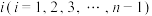 号同学未答对第一题,则第
号同学未答对第一题,则第 轮比赛失败,由第
轮比赛失败,由第 号同学继继续比赛;③若第
号同学继继续比赛;③若第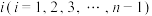 号同学答对第一题,则再答第二题,若该生答对第二题,则比赛在第
号同学答对第一题,则再答第二题,若该生答对第二题,则比赛在第 轮结束;若该生未答对第二题,则第
轮结束;若该生未答对第二题,则第 轮比赛失败,由第
轮比赛失败,由第 号同学继续答第二题,且以后比赛的同学不答第一题;④若比赛进行到了第
号同学继续答第二题,且以后比赛的同学不答第一题;④若比赛进行到了第 轮,则不管第
轮,则不管第 号同学答题情况,比赛结束.
号同学答题情况,比赛结束.(1)令随机变量
 表示
表示 名同学在第
名同学在第 轮比赛结束,当
轮比赛结束,当 时,求随机变量
时,求随机变量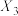 的分布列;
的分布列;(2)若把比赛规则③改为:若第
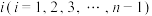 号同学未答对第二题,则第
号同学未答对第二题,则第 轮比赛失败,第
轮比赛失败,第 号同学重新从第一题开始作答.令随机变量
号同学重新从第一题开始作答.令随机变量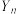 表示
表示 名挑战者在第
名挑战者在第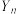 轮比赛结束.
轮比赛结束.①求随机变量
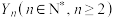 的分布列;
的分布列;②证明:
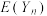 单调递增,且小于3.
单调递增,且小于3.
您最近一年使用:0次
2023-04-13更新
|
4619次组卷
|
9卷引用:云南省曲靖市第二中学2023届高三二模预测数学试题
云南省曲靖市第二中学2023届高三二模预测数学试题东北三省四市教研联合体2023届高三一模数学试题吉林省长春市2023届高三三模数学试题辽宁省大连市2023届高三一模数学试题(已下线)模块四 专题5 概率与统计(已下线)押新高考第19题 概率统计安徽省滁州市定远县育才学校2023届高考冲刺数学试卷(三)江苏省苏州工业园区星海实验中学2022-2023学年高二下学期5月阶段检测数学试题(已下线)专题8-2分布列综合归类-2
名校
5 . 设 是一个二维离散型随机变量,它们的一切可能取的值为
是一个二维离散型随机变量,它们的一切可能取的值为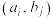 ,其中
,其中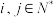 ,令
,令 ,称
,称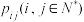 是二维离散型随机变量
是二维离散型随机变量 的联合分布列.与一维的情形相似,我们也习惯于把二维离散型随机变量的联合分布列写成下表形式:
的联合分布列.与一维的情形相似,我们也习惯于把二维离散型随机变量的联合分布列写成下表形式:
现有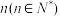 个相同的球等可能的放入编号为1,2,3的三个盒子中,记落下第1号盒子中的球的个数为X,落入第2号盒子中的球的个数为Y.
个相同的球等可能的放入编号为1,2,3的三个盒子中,记落下第1号盒子中的球的个数为X,落入第2号盒子中的球的个数为Y.
(1)当n=2时,求 的联合分布列;
的联合分布列;
(2)设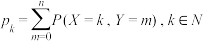 且
且 计算
计算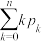 .
.
 是一个二维离散型随机变量,它们的一切可能取的值为
是一个二维离散型随机变量,它们的一切可能取的值为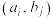 ,其中
,其中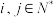 ,令
,令 ,称
,称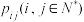 是二维离散型随机变量
是二维离散型随机变量 的联合分布列.与一维的情形相似,我们也习惯于把二维离散型随机变量的联合分布列写成下表形式:
的联合分布列.与一维的情形相似,我们也习惯于把二维离散型随机变量的联合分布列写成下表形式: |  |  |  | … |
 | 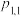 | 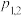 | 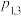 | … |
 | 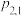 | 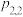 | 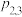 | … |
 | 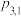 | 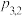 | 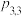 · · | … |
| … | … | … | … | … |
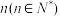 个相同的球等可能的放入编号为1,2,3的三个盒子中,记落下第1号盒子中的球的个数为X,落入第2号盒子中的球的个数为Y.
个相同的球等可能的放入编号为1,2,3的三个盒子中,记落下第1号盒子中的球的个数为X,落入第2号盒子中的球的个数为Y.(1)当n=2时,求
 的联合分布列;
的联合分布列;(2)设
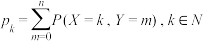 且
且 计算
计算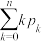 .
.
您最近一年使用:0次
2022-04-19更新
|
1483次组卷
|
6卷引用:云南省文山州广南县第一中学校2024届高三上学期第一次省统测数学模拟试题
云南省文山州广南县第一中学校2024届高三上学期第一次省统测数学模拟试题江苏省泰州市兴化市2022届高三下学期4月模拟考试数学试题(已下线)模块十 计数原理与统计概率-2(已下线)第8章 概率 单元综合检测(练习)(已下线)专题17 概率-2江苏省兴化中学2023-2024学年高二下学期期末适应性考试数学试题
名校
解题方法
6 . 春节期间某网络支付平台开展集“福”字活动:共有5种不同的“福”字电子卡,每完成一笔网络支付交易就能随机获赠一张“福”字卡,集齐5张不同的“福”字卡即可获奖.某网购平台上购买一袋脆干面,内随赠一张水浒传一百单八将的好汉卡,集齐完整一套好汉卡将获得生产商颁发的大奖(好汉卡一套共108张,每张上画有一将,每将都有很多张).
(1)若每完成一笔网络支付交易获赠每种“福”字卡的可能性相同.
①求获得第二种“福”字卡的概率;
②平均要完成多少笔交易才能集齐5个不同的“福”字卡?
(2)如果购买一袋脆干面随赠一张一百单八将的好汉卡中每一张的可能性是一样的,那么平均要购买多少袋脆干面才能获得生产商颁发的大奖?(结果保留到整数)
参考信息:
①.如果在一次试验中某事件发生的概率是p,那么在独立重复试验中,某事件第1次发生时所作试验的次数 的概率分本
的概率分本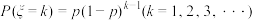 ,称
,称 服从几何分布,记作
服从几何分布,记作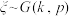 ;
; 的数学期望
的数学期望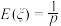 ;
;
②.若干个相互独立、且是按先后次序依次连续发生的随机变量之和的数学期望等于这些随机变量数学期望的之和;
③.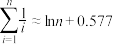 ,
, .
.
(1)若每完成一笔网络支付交易获赠每种“福”字卡的可能性相同.
①求获得第二种“福”字卡的概率;
②平均要完成多少笔交易才能集齐5个不同的“福”字卡?
(2)如果购买一袋脆干面随赠一张一百单八将的好汉卡中每一张的可能性是一样的,那么平均要购买多少袋脆干面才能获得生产商颁发的大奖?(结果保留到整数)
参考信息:
①.如果在一次试验中某事件发生的概率是p,那么在独立重复试验中,某事件第1次发生时所作试验的次数
 的概率分本
的概率分本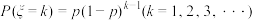 ,称
,称 服从几何分布,记作
服从几何分布,记作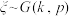 ;
; 的数学期望
的数学期望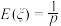 ;
;②.若干个相互独立、且是按先后次序依次连续发生的随机变量之和的数学期望等于这些随机变量数学期望的之和;
③.
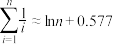 ,
, .
.
您最近一年使用:0次
2021-01-03更新
|
2081次组卷
|
7卷引用:云南省昆明市第一中学2021届高三年级12月月考理科数学试题
云南省昆明市第一中学2021届高三年级12月月考理科数学试题河南省新乡市辉县市一中2020-2021学年高二(培优班)下学期第一次阶段性考试数学理试题(已下线)7.4二项分布和超几何分布C卷(已下线)2023年四省联考变试题17-22(已下线)第四篇 概率与统计 专题7 常见分布 微点3 常见分布综合训练(已下线)第四篇 概率与统计 专题7 常见分布 微点2 其它分布(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点4 概率分布模型拓展【培优版】
名校
7 . 随着5G商用进程的不断加快,手机厂商之间围绕5G用户的争夺越来越激烈,5G手机也频频降价飞入寻常百姓家.某科技公司为了打开市场,计划先在公司进行“抽奖免费送5G手机”优惠活动方案的内部测试,测试成功后将在全市进行推广.
(1)公司内部测试的活动方案设置了第 次抽奖中奖的名额为
次抽奖中奖的名额为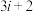 ,抽中的用户退出活动,同时补充新的用户,补充新用户的名额比上一次中奖用户的名额少2个.若某次抽奖,剩余全部用户均中奖,则活动结束.参加本次内部测试第一次抽奖的有15人,甲、乙均在其中.
,抽中的用户退出活动,同时补充新的用户,补充新用户的名额比上一次中奖用户的名额少2个.若某次抽奖,剩余全部用户均中奖,则活动结束.参加本次内部测试第一次抽奖的有15人,甲、乙均在其中.
①请求甲在第一次中奖和乙在第二次中奖的概率分别是多少?
②请求甲参加抽奖活动次数的分布列和期望?
(2)由于该活动方案在公司内部的测试非常顺利,现将在全市进行推广.报名参加第一次抽奖活动的有20万用户,该公司设置了第 次抽奖中奖的概率为
次抽奖中奖的概率为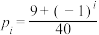 ,每次中奖的用户退出活动,同时补充相同人数的新用户,抽奖活动共进行
,每次中奖的用户退出活动,同时补充相同人数的新用户,抽奖活动共进行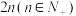 次.已知用户丙参加了第一次抽奖,并在这
次.已知用户丙参加了第一次抽奖,并在这 次抽奖活动中中奖了,在此条件下,求证:用户丙参加抽奖活动次数的均值小于
次抽奖活动中中奖了,在此条件下,求证:用户丙参加抽奖活动次数的均值小于 .
.
(1)公司内部测试的活动方案设置了第
 次抽奖中奖的名额为
次抽奖中奖的名额为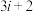 ,抽中的用户退出活动,同时补充新的用户,补充新用户的名额比上一次中奖用户的名额少2个.若某次抽奖,剩余全部用户均中奖,则活动结束.参加本次内部测试第一次抽奖的有15人,甲、乙均在其中.
,抽中的用户退出活动,同时补充新的用户,补充新用户的名额比上一次中奖用户的名额少2个.若某次抽奖,剩余全部用户均中奖,则活动结束.参加本次内部测试第一次抽奖的有15人,甲、乙均在其中.①请求甲在第一次中奖和乙在第二次中奖的概率分别是多少?
②请求甲参加抽奖活动次数的分布列和期望?
(2)由于该活动方案在公司内部的测试非常顺利,现将在全市进行推广.报名参加第一次抽奖活动的有20万用户,该公司设置了第
 次抽奖中奖的概率为
次抽奖中奖的概率为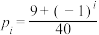 ,每次中奖的用户退出活动,同时补充相同人数的新用户,抽奖活动共进行
,每次中奖的用户退出活动,同时补充相同人数的新用户,抽奖活动共进行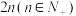 次.已知用户丙参加了第一次抽奖,并在这
次.已知用户丙参加了第一次抽奖,并在这 次抽奖活动中中奖了,在此条件下,求证:用户丙参加抽奖活动次数的均值小于
次抽奖活动中中奖了,在此条件下,求证:用户丙参加抽奖活动次数的均值小于 .
.
您最近一年使用:0次
2020-10-18更新
|
3182次组卷
|
11卷引用:云南省玉溪第一中学2023-2024学年高二下学期期末检测数学试题(特长级部)
云南省玉溪第一中学2023-2024学年高二下学期期末检测数学试题(特长级部)湖南省长沙市长郡中学2020-2021学年高三上学期月考(二)数学试题广东省实验中学2021届高三上学期第二次阶段性测试数学试题广东省实验中学2021届高三上学期11月阶段测试数学试题山东省淄博市淄博实验中学2020-2021学年高三上学期第二次模块考试数学试题(已下线)专题10-2 概率压轴大题(理)-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)(已下线)模块八 专题10 以概率与统计为背景的压轴大题广东省广州市2023届高三冲刺训练(三)数学试题广东省广州市培正中学2023届高三四模数学试题江苏省南通市如皋市2022-2023学年高二下学期期末模拟数学试题(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点3 概率统计与数列交汇综合训练【基础版】
8 . “工资条里显红利,个税新政人民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.2019年1月1日实施的个税新政主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.
新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
随机抽取某市1000名同一收入层级的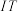 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.
假设该市该收入层级的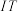 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的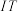 从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)设该市该收入层级的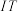 从业者2019年月缴个税为
从业者2019年月缴个税为 元,求
元,求 的分布列和期望;
的分布列和期望;
(2)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的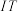 从业者各月少缴交的个税之和就超过2019年的月收入?
从业者各月少缴交的个税之和就超过2019年的月收入?
新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
| 旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
| 缴税级数 | 每月应纳税所得额(含税)=收入-个税起征点 | 税率(%) | 每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除 | 税率(%) |
| 1 | 不超过1500元部分 | 3 | 不超过3000元部分 | 3 |
| 2 | 超过1500元至4500元部分 | 10 | 超过3000元至12000元部分 | 10 |
| 3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
| 4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
| 5 | 超过35000元至55000元部分 | 30 | 超过35000元至55000元部分 | 30 |
| ··· | ··· | ··· | ··· | ··· |
随机抽取某市1000名同一收入层级的
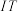 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的
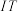 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的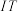 从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:(1)设该市该收入层级的
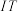 从业者2019年月缴个税为
从业者2019年月缴个税为 元,求
元,求 的分布列和期望;
的分布列和期望;(2)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的
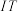 从业者各月少缴交的个税之和就超过2019年的月收入?
从业者各月少缴交的个税之和就超过2019年的月收入?
您最近一年使用:0次
2019-04-14更新
|
1989次组卷
|
5卷引用:云南省经开区2021届高三数学(理)模拟试题(一)



