名校
1 . 设集合 为
为 元数集,若
元数集,若 的2个非空子集
的2个非空子集 满足:
满足: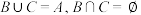 ,则称
,则称 为
为 的一个二阶划分.记
的一个二阶划分.记 中所有元素之和为
中所有元素之和为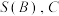 中所有元素之和为
中所有元素之和为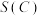 .
.
(1)若 ,求
,求 的一个二阶划分,使得
的一个二阶划分,使得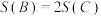 ;
;
(2)若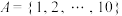 .求证:不存在
.求证:不存在 的二阶划分
的二阶划分 满足
满足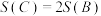 ;
;
(3)若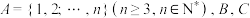 为
为 的一个二阶划分,满足:①若
的一个二阶划分,满足:①若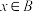 ,则
,则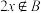 ;②若
;②若 ,则
,则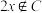 .记
.记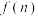 为符合条件的
为符合条件的 的个数,求
的个数,求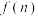 的解析式.
的解析式.
 为
为 元数集,若
元数集,若 的2个非空子集
的2个非空子集 满足:
满足: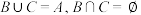 ,则称
,则称 为
为 的一个二阶划分.记
的一个二阶划分.记 中所有元素之和为
中所有元素之和为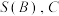 中所有元素之和为
中所有元素之和为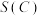 .
.(1)若
 ,求
,求 的一个二阶划分,使得
的一个二阶划分,使得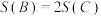 ;
;(2)若
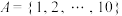 .求证:不存在
.求证:不存在 的二阶划分
的二阶划分 满足
满足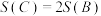 ;
;(3)若
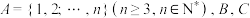 为
为 的一个二阶划分,满足:①若
的一个二阶划分,满足:①若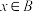 ,则
,则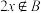 ;②若
;②若 ,则
,则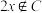 .记
.记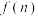 为符合条件的
为符合条件的 的个数,求
的个数,求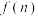 的解析式.
的解析式.
您最近一年使用:0次
2023-07-17更新
|
806次组卷
|
5卷引用:重庆市南开中学校2023-2024学年高一上学期开学考试数学试题
重庆市南开中学校2023-2024学年高一上学期开学考试数学试题北京市顺义区2022-2023学年高一下学期期末质量监测数学试题(已下线)难关必刷01集合的综合问题(3种题型40题专项训练)-【满分全攻略】(人教A版2019必修第一册)(已下线)第三章 函数的概念与性质-【优化数学】单元测试能力卷(人教A版2019)(已下线)专题03 函数的概念与性质3-2024年高一数学寒假作业单元合订本
2 . 有限数列 :
: ,
, ,…,
,…, .(
.( )同时满足下列两个条件:
)同时满足下列两个条件:
①对于任意的 ,
, (
( ),
), ;
;
②对于任意的 ,
, ,
, (
(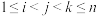 ),
),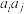 ,
,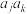 ,
,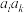 ,三个数中至少有一个数是数列
,三个数中至少有一个数是数列 中的项.
中的项.
(1)若 ,且
,且 ,
, ,
,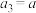 ,
, ,求
,求 的值;
的值;
(2)证明: ,
, ,
, 不可能是数列
不可能是数列 中的项;
中的项;
(3)求 的最大值.
的最大值.
 :
: ,
, ,…,
,…, .(
.( )同时满足下列两个条件:
)同时满足下列两个条件:①对于任意的
 ,
, (
( ),
), ;
;②对于任意的
 ,
, ,
, (
(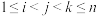 ),
),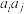 ,
,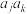 ,
,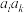 ,三个数中至少有一个数是数列
,三个数中至少有一个数是数列 中的项.
中的项.(1)若
 ,且
,且 ,
, ,
,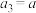 ,
, ,求
,求 的值;
的值;(2)证明:
 ,
, ,
, 不可能是数列
不可能是数列 中的项;
中的项;(3)求
 的最大值.
的最大值.
您最近一年使用:0次
2021-11-19更新
|
1291次组卷
|
10卷引用:重庆市缙云教育联盟2022届高三上学期第O次诊断性检测数学试题
重庆市缙云教育联盟2022届高三上学期第O次诊断性检测数学试题2015届北京市海淀区高三下学期期中练习(一模)理科数学试卷北京市北京师范大学第二附属中学2019-2020学年高二上学期期中数学试卷北京市第五十七中学2019-2020学年高二上学期期中考试数学试题(已下线)北京市第四中学2022届高三下学期(三模)保温练习数学试题北京卷专题18数列(解答题)(已下线)北京市第四中学2023届高三数学保温测试试题北京市十一学校2022届高三下学期2月诊断数学试题北京市第八中学2024届高三上学期10月练习数学试题北京市汇文中学教育集团2023-2024学年高三下学期开学考数学试题
名校
3 . 已知集合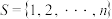 (
( 且
且 ),
), ,且
,且 .若对任意
.若对任意 ,
, ,当
,当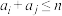 时,存在
时,存在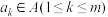 ,使得
,使得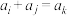 ,则称
,则称 是
是 的
的 元完美子集.
元完美子集.
(1)判断下列集合是否是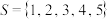 的3元完美子集,并说明理由;
的3元完美子集,并说明理由;
①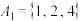 ;
;
②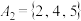 ;
;
(2)若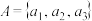 是
是 的3元完美子集,求
的3元完美子集,求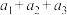 的最小值;
的最小值;
(3)若 是
是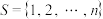 (
( 且
且 )的
)的 元完美子集,求证:
元完美子集,求证: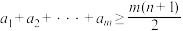 .
.
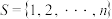 (
( 且
且 ),
), ,且
,且 .若对任意
.若对任意 ,
, ,当
,当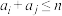 时,存在
时,存在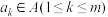 ,使得
,使得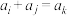 ,则称
,则称 是
是 的
的 元完美子集.
元完美子集.(1)判断下列集合是否是
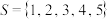 的3元完美子集,并说明理由;
的3元完美子集,并说明理由;①
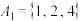 ;
; ②
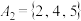 ;
;(2)若
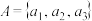 是
是 的3元完美子集,求
的3元完美子集,求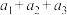 的最小值;
的最小值;(3)若
 是
是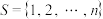 (
( 且
且 )的
)的 元完美子集,求证:
元完美子集,求证: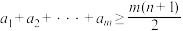 .
.
您最近一年使用:0次
2022-05-12更新
|
844次组卷
|
4卷引用:重庆市杨家坪中学2022-2023学年高一上学期10月月考数学试题
重庆市杨家坪中学2022-2023学年高一上学期10月月考数学试题北京师范大学附属中学2021-2022学年高一下学期期中考试数学试题(已下线)专题16 数列新定义题的解法 微点2 数列新定义题综合训练北京市第二中学2022—2023学年高一下学期第六学段阶段性考试数学试题
4 . 已知集合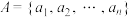 中的元素都是正整数,且
中的元素都是正整数,且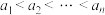 .若对任意
.若对任意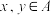 ,且
,且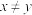 ,都有
,都有 成立,则称集合A具有性质
成立,则称集合A具有性质 .
.
(1)判断集合 是否具有性质
是否具有性质 ;
;
(2)已知集合A具有性质 ,求证:
,求证: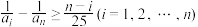 ;
;
(3)证明: 是无理数.
是无理数.
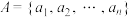 中的元素都是正整数,且
中的元素都是正整数,且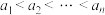 .若对任意
.若对任意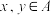 ,且
,且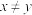 ,都有
,都有 成立,则称集合A具有性质
成立,则称集合A具有性质 .
.(1)判断集合
 是否具有性质
是否具有性质 ;
;(2)已知集合A具有性质
 ,求证:
,求证: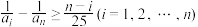 ;
;(3)证明:
 是无理数.
是无理数.
您最近一年使用:0次
2023-10-18更新
|
179次组卷
|
3卷引用:重庆市字水中学2024-2025学年高一上学期10月月考数学试题
名校
5 . 设 均为正实数,反证法证明:
均为正实数,反证法证明: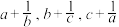 至少有一个不小于2.
至少有一个不小于2.
 均为正实数,反证法证明:
均为正实数,反证法证明: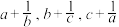 至少有一个不小于2.
至少有一个不小于2.
您最近一年使用:0次
2020-02-15更新
|
609次组卷
|
10卷引用:重庆市江津第六中学2018-2019学年高二下学期期中(文)数学试题
重庆市江津第六中学2018-2019学年高二下学期期中(文)数学试题2016-2017学年河南省洛阳市高二下学期期中考试数学(文)试卷陕西省延安市吴起高级中学2019-2020学年高二下学期第一次质量检测数学(理)试题福建省莆田第二十四中学2019-2020学年高二下学期返校测试数学(文)试题甘肃省张掖市山丹县第一中学2019-2020学年高二下学期期中考试数学(文)试题安徽省池州市东至二中2019-2020学年高二下学期6月月考理科数学试题(已下线)专题04+常用逻辑用语(2)(反证法)-2020-2021学年新教材高一数学秋季辅导讲义(沪教版2020)(已下线)第04讲 常用逻辑用语(3大考点)(2)(已下线)专题04常用逻辑用语-【倍速学习法】(沪教版2020必修第一册)(已下线)第一章 集合与逻辑(知识清单+典型例题)-【满分全攻略】(沪教版2020必修第一册)
6 . (1)求证: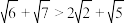
(2)已知 ,
, ,且
,且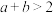 ,求证:
,求证: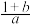 和
和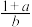 中至少有一个小于2.
中至少有一个小于2.
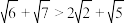
(2)已知
 ,
, ,且
,且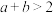 ,求证:
,求证: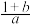 和
和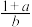 中至少有一个小于2.
中至少有一个小于2.
您最近一年使用:0次
2016-12-04更新
|
1552次组卷
|
7卷引用:重庆市万州第二高级中学2018-2019学年高二下学期期中(理)数学试题
重庆市万州第二高级中学2018-2019学年高二下学期期中(理)数学试题2015-2016学年山东曲阜师大附中高二下学期期中数学(理)试卷2015-2016学年山东曲阜师大附中高二下学期期中数学(文)试卷【全国市级联考】山东省菏泽市2017-2018学年高二下学期期中考试数学(理)试题【校级联考】河南省郑州市2018-2019学年下期期中高二年级八校联考试题文科数学试题河南省南阳市第一中学2018-2019学年高二下学期第一次月考数学(理)试题(已下线)专题04+常用逻辑用语(2)(反证法)-2020-2021学年新教材高一数学秋季辅导讲义(沪教版2020)
7 . (1)用分析法证明:当 ,
,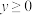 时,
时,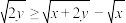 ;
;
(2)证明:对任意 ,
, ,
,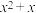 ,
,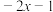 这
这 个值至少有一个不小于
个值至少有一个不小于 .
.
 ,
,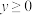 时,
时,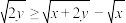 ;
;(2)证明:对任意
 ,
, ,
,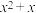 ,
,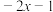 这
这 个值至少有一个不小于
个值至少有一个不小于 .
.
您最近一年使用:0次
2020-03-17更新
|
259次组卷
|
3卷引用:重庆市万州二中2019-2020学年高二下学期开学考试(4月)数学试题
真题
8 . 设 个不全相等的正数
个不全相等的正数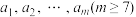 依次围成一个圆圈.
依次围成一个圆圈.
(Ⅰ)若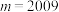 ,且
,且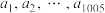 是公差为
是公差为 的等差数列,而
的等差数列,而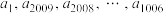 是公比为
是公比为 的等比数列;数列
的等比数列;数列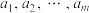 的前
的前 项和
项和 满足:
满足: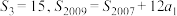 ,求通项
,求通项 ;
;
(Ⅱ)若每个数 是其左右相邻两数平方的等比中项,求证:
是其左右相邻两数平方的等比中项,求证: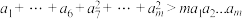 .
.
 个不全相等的正数
个不全相等的正数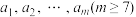 依次围成一个圆圈.
依次围成一个圆圈.(Ⅰ)若
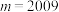 ,且
,且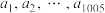 是公差为
是公差为 的等差数列,而
的等差数列,而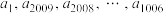 是公比为
是公比为 的等比数列;数列
的等比数列;数列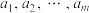 的前
的前 项和
项和 满足:
满足: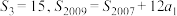 ,求通项
,求通项 ;
;(Ⅱ)若每个数
 是其左右相邻两数平方的等比中项,求证:
是其左右相邻两数平方的等比中项,求证: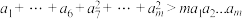 .
.
您最近一年使用:0次
13-14高二下·重庆·期中
解题方法
9 . 给定数列
(1)判断 是否为有理数,证明你的结论;
是否为有理数,证明你的结论;
(2)是否存在常数 .使
.使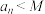 对
对 都成立? 若存在,找出
都成立? 若存在,找出 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由.

(1)判断
 是否为有理数,证明你的结论;
是否为有理数,证明你的结论;(2)是否存在常数
 .使
.使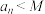 对
对 都成立? 若存在,找出
都成立? 若存在,找出 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由.
您最近一年使用:0次

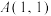 是椭圆
是椭圆 上一点,
上一点, 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足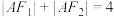
 最大时,求证
最大时,求证 不对称.
不对称.


