解题方法
1 . 已知数列 满足,
满足, ,
,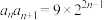 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:数列 中的任意三项均不能构成等差数列.
中的任意三项均不能构成等差数列.
 满足,
满足, ,
,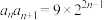 ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)证明:数列
 中的任意三项均不能构成等差数列.
中的任意三项均不能构成等差数列.
您最近一年使用:0次
2023-04-20更新
|
3264次组卷
|
5卷引用:广东省深圳市2023届高三二模数学试题
名校
2 . 已知有限集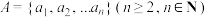 ,如果
,如果 中的元素
中的元素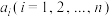 满足
满足 ,就称
,就称 为“完美集”.
为“完美集”.
(1)判断:集合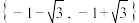 是否是“完美集”并说明理由;
是否是“完美集”并说明理由;
(2)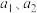 是两个不同的正数,且
是两个不同的正数,且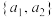 是“完美集”,求证:
是“完美集”,求证: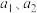 至少有一个大于2;
至少有一个大于2;
(3)若 为正整数,求:“完美集”
为正整数,求:“完美集” .
.
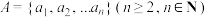 ,如果
,如果 中的元素
中的元素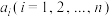 满足
满足 ,就称
,就称 为“完美集”.
为“完美集”.(1)判断:集合
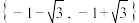 是否是“完美集”并说明理由;
是否是“完美集”并说明理由;(2)
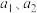 是两个不同的正数,且
是两个不同的正数,且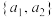 是“完美集”,求证:
是“完美集”,求证: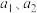 至少有一个大于2;
至少有一个大于2;(3)若
 为正整数,求:“完美集”
为正整数,求:“完美集” .
.
您最近一年使用:0次
2024-09-09更新
|
1850次组卷
|
16卷引用:广东省广州四十一中2024-2025学年高一上学期10月月考数学试题
广东省广州四十一中2024-2025学年高一上学期10月月考数学试题上海市延安中学2024-2025学年高一上学期新生综合素质检测数学试卷山东省青岛市第五十八中学2024-2025学年高一上学期第一次月考数学试题上海市洋泾中学2024-2025学年高一上学期第一次月考数学试卷黑龙江省黑河市嫩江市高级中学2024-2025学年高一上学期第一次阶段性考试数学试卷山东省新泰市第一中学2024-2025学年高一上学期过程适应性训练数学试题江苏省扬州市高邮中学2024-2025学年高一上学期10月检测数学试题考点考题点点通——第一章集合与常用逻辑用语01江苏省无锡市运河实验中学2024-2025学年高一上学期10月月考数学试卷北京市西城区北京师范大学附属实验中学2024-2025学年高一上学期阶段练习一(10月)数学试题上海市敬业中学2024-2025学年高一上学期10月月考数学试卷河南省淮滨高级中学2024-2025学年高一上学期10月月考数学试题江苏省东海高级中学城北校区2024-2025学年高一上学期第一次月考数学试题山东省泰安市泰山国际学校2024—2025学年高一上学期10月月考数学试题江苏省苏州市苏苑高级中学2024-2025学年高一上学期10月月考数学试题福建省莆田市秀屿区实验中学2024-2025学年高一上学期10月月考数学试卷
名校
3 . 已知 是各项均为正整数的无穷递增数列,对于
是各项均为正整数的无穷递增数列,对于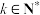 ,定义集合
,定义集合 ,设
,设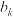 为集合
为集合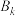 中的元素个数,若
中的元素个数,若 时,规定
时,规定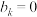 .
.
(1)若 ,写出
,写出 及
及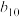 的值;
的值;
(2)若数列 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;
(3)设集合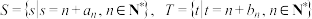 ,求证:
,求证: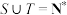 且
且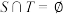 .
.
 是各项均为正整数的无穷递增数列,对于
是各项均为正整数的无穷递增数列,对于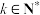 ,定义集合
,定义集合 ,设
,设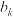 为集合
为集合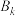 中的元素个数,若
中的元素个数,若 时,规定
时,规定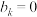 .
.(1)若
 ,写出
,写出 及
及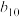 的值;
的值;(2)若数列
 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;(3)设集合
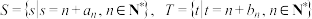 ,求证:
,求证: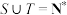 且
且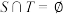 .
.
您最近一年使用:0次
2024-01-21更新
|
1667次组卷
|
7卷引用:广东省江门市开平市忠源纪念中学2024届高三下学期高考冲刺考试(一)数学试卷
广东省江门市开平市忠源纪念中学2024届高三下学期高考冲刺考试(一)数学试卷北京市朝阳区2024届高三上学期期末数学试题(已下线)专题1 集合新定义题(九省联考第19题模式)讲(已下线)2024年高考数学二轮复习测试卷(北京专用)(已下线)黄金卷01(2024新题型)(已下线)微考点4-1 新高考新试卷结构压轴题新定义数列试题分类汇编江苏省常州市华罗庚中学2024届高三下学期4月二模训练数学试卷
名校
解题方法
4 . 已知正项数列 ,其前n项和
,其前n项和 满足
满足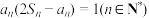 .
.
(1)求证:数列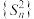 是等差数列,并求出
是等差数列,并求出 的表达式;
的表达式;
(2)数列 中是否存在连续三项
中是否存在连续三项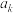 ,
,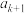 ,
,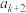 ,使得
,使得 ,
,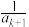 ,
, 构成等差数列?请说明理由.
构成等差数列?请说明理由.
 ,其前n项和
,其前n项和 满足
满足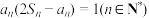 .
.(1)求证:数列
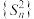 是等差数列,并求出
是等差数列,并求出 的表达式;
的表达式;(2)数列
 中是否存在连续三项
中是否存在连续三项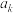 ,
,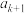 ,
,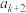 ,使得
,使得 ,
,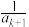 ,
, 构成等差数列?请说明理由.
构成等差数列?请说明理由.
您最近一年使用:0次
2022-03-30更新
|
2658次组卷
|
5卷引用:广东省2022届高三一模数学试题
广东省2022届高三一模数学试题广东省汕头市金山中学2021-2022学年高二下学期期中数学试题(已下线)必刷卷04-2022年高考数学考前信息必刷卷(新高考地区专用)(已下线)广东省2022届高三一模数学试题变式题17-22浙江名校联盟2022-2023学年高二下学期期中联考数学试题(B卷)
5 . 定义两个 维向量
维向量 ,
, 的数量积
的数量积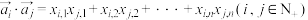 ,
,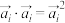 ,记
,记 为
为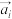 的第k个分量(
的第k个分量( 且
且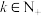 ).如三维向量
).如三维向量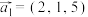 ,其中
,其中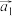 的第2分量
的第2分量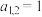 .若由
.若由 维向量组成的集合A满足以下三个条件:①集合中含有n个n维向量作为元素;②集合中每个元素的所有分量取0或1;③集合中任意两个元素
维向量组成的集合A满足以下三个条件:①集合中含有n个n维向量作为元素;②集合中每个元素的所有分量取0或1;③集合中任意两个元素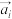 ,
,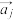 ,满足
,满足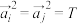 (T为常数)且
(T为常数)且 .则称A为T的完美n维向量集.
.则称A为T的完美n维向量集.
(1)求2的完美3维向量集;
(2)判断是否存在完美4维向量集,并说明理由;
(3)若存在A为T的完美n维向量集,求证:A的所有元素的第k分量和 .
.
 维向量
维向量 ,
, 的数量积
的数量积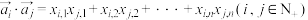 ,
,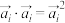 ,记
,记 为
为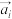 的第k个分量(
的第k个分量( 且
且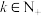 ).如三维向量
).如三维向量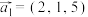 ,其中
,其中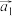 的第2分量
的第2分量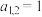 .若由
.若由 维向量组成的集合A满足以下三个条件:①集合中含有n个n维向量作为元素;②集合中每个元素的所有分量取0或1;③集合中任意两个元素
维向量组成的集合A满足以下三个条件:①集合中含有n个n维向量作为元素;②集合中每个元素的所有分量取0或1;③集合中任意两个元素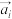 ,
,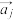 ,满足
,满足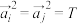 (T为常数)且
(T为常数)且 .则称A为T的完美n维向量集.
.则称A为T的完美n维向量集.(1)求2的完美3维向量集;
(2)判断是否存在完美4维向量集,并说明理由;
(3)若存在A为T的完美n维向量集,求证:A的所有元素的第k分量和
 .
.
您最近一年使用:0次
2024-03-27更新
|
956次组卷
|
4卷引用:广东省汕头市潮阳区河溪中学2023-2024学年高三下学期第二学月质检数学试题
广东省汕头市潮阳区河溪中学2023-2024学年高三下学期第二学月质检数学试题2024届江西省九江市二模数学试题(已下线)拔高点突破01 集合背景下的新定义压轴解答题(四大题型)(已下线)专题7 线性代数、抽象代数与数论背景的新定义压轴大题(过关集训)
解题方法
6 . 已知数列 中
中 ,其前
,其前 项和记为
项和记为 ,且满足
,且满足 .
.
(1)求数列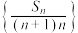 的通项公式;
的通项公式;
(2)设无穷数列 ,
, ,…
,… ,…对任意自然数
,…对任意自然数 和
和 ,不等式
,不等式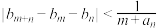 均成立,证明:数列
均成立,证明:数列 是等差数列.
是等差数列.
 中
中 ,其前
,其前 项和记为
项和记为 ,且满足
,且满足 .
.(1)求数列
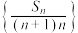 的通项公式;
的通项公式;(2)设无穷数列
 ,
, ,…
,… ,…对任意自然数
,…对任意自然数 和
和 ,不等式
,不等式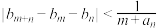 均成立,证明:数列
均成立,证明:数列 是等差数列.
是等差数列.
您最近一年使用:0次
2023-03-16更新
|
668次组卷
|
3卷引用:广东省韶关市武江区广东北江实验学校2022-2023学年高二下学期第一次(3月)月考数学试题
广东省韶关市武江区广东北江实验学校2022-2023学年高二下学期第一次(3月)月考数学试题江苏省南京市中华、东外、镇江三校2022-2023学年高三下学期3月联考数学试题(已下线)第4章 数列 单元综合检测(重点)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
真题
名校
7 . 等差数列 的前
的前 项和为
项和为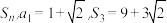 .
.
(Ⅰ)求数列 的通项
的通项 与前
与前 项和
项和 ;
;
(Ⅱ)设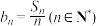 ,求证:数列
,求证:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
 的前
的前 项和为
项和为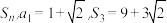 .
.(Ⅰ)求数列
 的通项
的通项 与前
与前 项和
项和 ;
;(Ⅱ)设
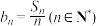 ,求证:数列
,求证:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
您最近一年使用:0次
2019-01-30更新
|
3462次组卷
|
27卷引用:广东省华南师范大学附属中学2018-2019学年上学期高二年级期末数学试题
广东省华南师范大学附属中学2018-2019学年上学期高二年级期末数学试题2007年普通高等学校招生全国统一考试理科数学卷(福建)(已下线)2011届江西省师大附中高三上学期期中考试数学理卷(已下线)2011届江苏省无锡一中高三上学期期中考试数学试卷(已下线)2011届江苏省无锡市辅仁高级中学高三上学期期中数学卷(已下线)2012届山东省济宁市汶上一中高三11月月考理科数学试卷(已下线)2012届江西省吉水二中高三第四次月考理科数学试卷2015-2016学年贵州遵义航天高中高二3月考文科数学试卷2015-2016湖南常德石门一中高二下第一次月考文科数学卷2015-2016学年辽宁省鞍山一中高二下期中理科数学试卷高中数学人教A版选修2-2 第二章 推理与证明 2.2.2 反证法(2)湖北省部分重点中学2017-2018学年高二下学期期中考试数学(文)试题河南省南阳市2018-2019学年高二下学期期末考试数学(文)试题(已下线)专题11.2 直接证明与间接证明(讲)【文】-《2020年高考一轮复习讲练测》(已下线)专题11.5 第十一章 推理与证明、算法、复数(单元测试)(测)【文】-《2020年高考一轮复习讲练测》(已下线)专题01 等差与等比数列的基本量的计算(第二篇)-备战2020年高考数学大题精做之解答题题型全覆盖沪教版(上海) 高三年级 新高考辅导与训练 第四章 数列与数学归纳法 一、等差数列与等比数列安徽省池州市第一中学2019-2020学年高二下学期期中教学质量检测数学(理)试题(已下线)专题12.2 直接证明与间接证明、数学归纳法(精练)-2021届高考数学(文)一轮复习讲练测(已下线)专题12.2 直接证明与间接证明、数学归纳法(精讲)-2021年高考数学(理)一轮复习讲练测(已下线)考点57 推理与证明-备战2021年高考数学(理)一轮复习考点一遍过 (已下线)考点49 推理与证明-备战2021年高考数学(文)一轮复习考点一遍过(已下线)考点43 直接证明与间接证明-备战2022年高考数学(理)一轮复习考点微专题(已下线)考点22 等差数列及其前n项和-备战2022年高考数学(理)一轮复习考点帮高中数学解题兵法 第一百讲 正难则反2007年普通高等学校招生考试数学(理)试题(福建卷)(已下线)专题6 等比数列的判断(证明)方法 微点1 定义法、等比中项法
真题
名校
8 . 设 ,
, ,且
,且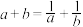 .
.
证明:(1) ;
;
(2)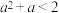 与
与 不可能同时成立.
不可能同时成立.
 ,
, ,且
,且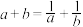 .
.证明:(1)
 ;
;(2)
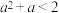 与
与 不可能同时成立.
不可能同时成立.
您最近一年使用:0次
2016-12-03更新
|
4950次组卷
|
33卷引用:【全国百强校】广东省中山市第一中学2017-2018学年高二下学期第三次统测(期末模拟)数学(文)试题
【全国百强校】广东省中山市第一中学2017-2018学年高二下学期第三次统测(期末模拟)数学(文)试题2015年全国普通高等学校招生统一考试理科数学(湖南卷)2016-2017学年江西省上饶市高二上学期期末考试理数试卷陕西省榆林市2018届高考模拟第一次测试理科数学试题陕西省榆林市2018届高考模拟第一次测试文科数学试题(已下线)2019年3月20日 《每日一题》理数选修2-2-反证法(1)【校级联考】河南省开封市、商丘市九校2018-2019学年高二下学期期中联考数学(文)试题安徽省蚌埠市第二中学2016-2017学年高二下学期期中考试数学(文)试题步步高高二数学暑假作业:【文】作业19 推理与证明、算法初步、复数上海市复旦大学附属中学2019-2020学年高一上学期期中数学试题(已下线)专题7.3 基本不等式及其应用(讲)-江苏版《2020年高考一轮复习讲练测》专题11+不等式选讲-2021高考数学(理)高频考点、热点题型归类强化(已下线)【新教材精创】2.2.4均值不等式及其应用练习(2)-人教B版高中数学必修第一册2020届陕西省商洛市丹凤中学高三第一次模拟考试数学(理)试题(已下线)上海市浦东新区华师大二附中2020-2021学年高一上学期期中数学试题(已下线)上海市华东师范大学第二附属中学2020-2021学年高一上学期期中数学试题(已下线)调研测试四(B卷 滚动提升检测)-2021年高考数学(理)一轮复习单元滚动双测卷上海市上海中学2020-2021学年高一上学期12月月考数学试题(已下线)专题14.2 不等式的证明(精练)-2021届高考数学(理)一轮复习讲练测(已下线)专题12.2 直接证明与间接证明、数学归纳法(精讲)-2021年高考数学(理)一轮复习讲练测(已下线)专题12.2 直接证明与间接证明 (精讲)-2021届高考数学(文)一轮复习学与练(已下线)专题14.2 不等式的证明(精练)-2021届高考数学(文)一轮复习学与练(已下线)专题14.2 不等式的证明(精练)-2021年高考数学(理)一轮复习学与练上海市嘉定一中2020-2021学年高一上学期12月月考数学试题安徽省亳州市涡阳县育萃高级中学2020-2021学年高二下学期第一次月考数学(文)试题安徽省黄山市屯溪第一中学2020-2021学年高二下学期期中理科数学试题(已下线)考点43 直接证明与间接证明-备战2022年高考数学(理)一轮复习考点微专题陕西省咸阳市武功县普集高中2021-2022学年高二下学期第一次月考理科数学试题湖北省襄阳市第五中学2022-2023学年高一上学期12月月考数学试题(已下线)【新教材精创】2.2.4 均值不等式及其应用 练习(2)-人教B版高中数学必修第一册(已下线)专题27 不等式选讲(文理通用)专题39不等式选讲(已下线)考点04 基本不等式及其应用--高考数学100个黄金考点(2025届)【练】
9 . 已知集合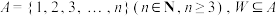 且
且 中元素的个数为
中元素的个数为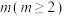 .若存在
.若存在 ,
,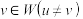 得
得 为2的正整数指数幂,则称
为2的正整数指数幂,则称 为
为 的弱
的弱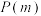 子集;若对任意的
子集;若对任意的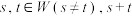 均为2的正整数指数幂,则称
均为2的正整数指数幂,则称 为
为 的强
的强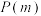 子集.
子集.
(1)请判断集合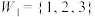 和
和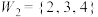 是否为
是否为 的弱
的弱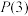 子集,并说明理由;
子集,并说明理由;
(2)是否存在 的强
的强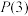 子集?若存在,请写出一个例子;若不存在,请说明理由;
子集?若存在,请写出一个例子;若不存在,请说明理由;
(3)若 ,且
,且 的任意一个元素个数为
的任意一个元素个数为 的子集都是
的子集都是 的弱
的弱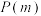 子集,求
子集,求 的最小值.
的最小值.
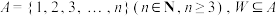 且
且 中元素的个数为
中元素的个数为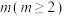 .若存在
.若存在 ,
,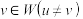 得
得 为2的正整数指数幂,则称
为2的正整数指数幂,则称 为
为 的弱
的弱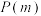 子集;若对任意的
子集;若对任意的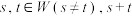 均为2的正整数指数幂,则称
均为2的正整数指数幂,则称 为
为 的强
的强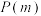 子集.
子集.(1)请判断集合
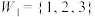 和
和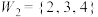 是否为
是否为 的弱
的弱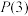 子集,并说明理由;
子集,并说明理由;(2)是否存在
 的强
的强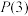 子集?若存在,请写出一个例子;若不存在,请说明理由;
子集?若存在,请写出一个例子;若不存在,请说明理由;(3)若
 ,且
,且 的任意一个元素个数为
的任意一个元素个数为 的子集都是
的子集都是 的弱
的弱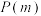 子集,求
子集,求 的最小值.
的最小值.
您最近一年使用:0次
2024-07-26更新
|
390次组卷
|
3卷引用:广东省广州市华南师范大学附属中学2024-2025学年高二上学期10月月考数学试卷
真题
解题方法
10 . A是由定义在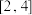 上且满足如下条件的函数
上且满足如下条件的函数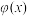 组成的集合:①对任意的
组成的集合:①对任意的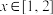 ,都有
,都有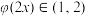 ;②存在常数
;②存在常数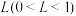 ,使得对任意的
,使得对任意的 ,都有
,都有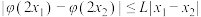 .
.
(1)设 ,证明:
,证明: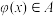 ;
;
(2)设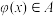 ,如果存在
,如果存在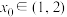 ,使得
,使得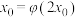 ,那么这样的
,那么这样的 是唯一的;
是唯一的;
(3)设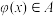 ,任取
,任取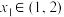 ,令
,令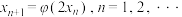 ,证明:给定正整数k,对任意的正整数p,不等式
,证明:给定正整数k,对任意的正整数p,不等式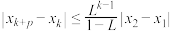 成立.
成立.
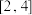 上且满足如下条件的函数
上且满足如下条件的函数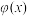 组成的集合:①对任意的
组成的集合:①对任意的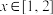 ,都有
,都有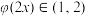 ;②存在常数
;②存在常数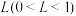 ,使得对任意的
,使得对任意的 ,都有
,都有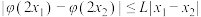 .
.(1)设
 ,证明:
,证明: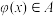 ;
;(2)设
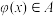 ,如果存在
,如果存在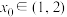 ,使得
,使得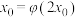 ,那么这样的
,那么这样的 是唯一的;
是唯一的;(3)设
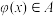 ,任取
,任取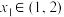 ,令
,令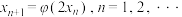 ,证明:给定正整数k,对任意的正整数p,不等式
,证明:给定正整数k,对任意的正整数p,不等式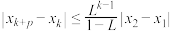 成立.
成立.
您最近一年使用:0次



