1 . 设 为正整数,集合
为正整数,集合 对于
对于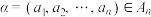 ,设集合
,设集合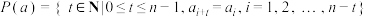 .
.
(1)若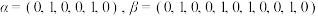 ,写出集合
,写出集合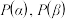 ;
;
(2)若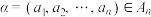 ,且
,且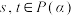 满足
满足 令
令  ,求证:
,求证: 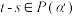 ;
;
(3)若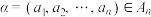 ,且
,且 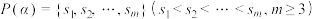 ,求证:
,求证: 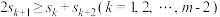 .
.
 为正整数,集合
为正整数,集合 对于
对于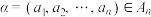 ,设集合
,设集合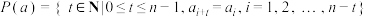 .
.(1)若
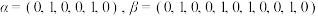 ,写出集合
,写出集合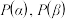 ;
;(2)若
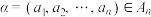 ,且
,且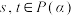 满足
满足 令
令  ,求证:
,求证: 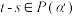 ;
;(3)若
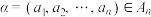 ,且
,且 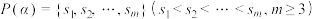 ,求证:
,求证: 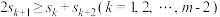 .
.
您最近半年使用:0次
名校
2 . 设非空数集M,对于M中的任意两个元素,如果满足:①两个元素之和属于M ②两个元素之差属于M.③两个元素之积属于M ④两个元素之商(分母不为零)也属于M.定义:满足条件①②③的数集M为数环(即数环对于加、减、乘运算封闭);满足④的数环M为数域(即数域对于加、减、乘、除运算封闭).
(1)判断自然数集N、整数集Z、有理数集Q、实数集R、复数集C是不是数环,假如该集合是数环,那么它是不是数域(无需说明理由);
(2)若M是一个数环,证明: ;若S是一个数域,证明:
;若S是一个数域,证明: ;
;
(3)设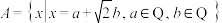 ,证明A是数域.
,证明A是数域.
(1)判断自然数集N、整数集Z、有理数集Q、实数集R、复数集C是不是数环,假如该集合是数环,那么它是不是数域(无需说明理由);
(2)若M是一个数环,证明:
 ;若S是一个数域,证明:
;若S是一个数域,证明: ;
;(3)设
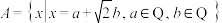 ,证明A是数域.
,证明A是数域.
您最近半年使用:0次
名校
3 . 对称变换在对称数学中具有重要的研究意义.若一个平面图形K在m(旋转变换或反射变换)的作用下仍然与原图形重合,就称K具有对称性,并记m为K的一个对称变换.例如,正三角形R在 (绕中心O作120°的旋转)的作用下仍然与R重合(如图1图2所示),所以
(绕中心O作120°的旋转)的作用下仍然与R重合(如图1图2所示),所以 是R的一个对称变换,考虑到变换前后R的三个顶点间的对应关系,记
是R的一个对称变换,考虑到变换前后R的三个顶点间的对应关系,记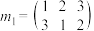 ;又如,R在
;又如,R在 (关于对称轴
(关于对称轴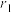 所在直线的反射)的作用下仍然与R重合(如图1图3所示),所以
所在直线的反射)的作用下仍然与R重合(如图1图3所示),所以 也是R的一个对称变换,类似地,记
也是R的一个对称变换,类似地,记 .记正三角形R的所有对称变换构成集合S.一个非空集合G对于给定的代数运算.来说作成一个群,假如同时满足:
.记正三角形R的所有对称变换构成集合S.一个非空集合G对于给定的代数运算.来说作成一个群,假如同时满足:
I.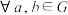 ,
, ;
;
II. ,
, ;
;
Ⅲ. ,
,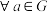 ,
, ;
;
Ⅳ.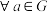 ,
,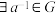 ,
,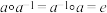 .
.
对于一个群G,称Ⅲ中的e为群G的单位元,称Ⅳ中的 为a在群G中的逆元.一个群G的一个非空子集H叫做G的一个子群,假如H对于G的代数运算
为a在群G中的逆元.一个群G的一个非空子集H叫做G的一个子群,假如H对于G的代数运算 来说作成一个群.
来说作成一个群.
(2)同一个对称变换的符号语言表达形式不唯一,如 .对于集合S中的元素,定义一种新运算*,规则如下:
.对于集合S中的元素,定义一种新运算*,规则如下: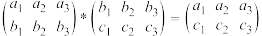 ,
, .
.
①证明集合S对于给定的代数运算*来说作成一个群;
②已知H是群G的一个子群,e,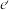 分别是G,H的单位元,
分别是G,H的单位元,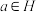 ,
, ,
, 分别是a在群G,群H中的逆元.猜想e,
分别是a在群G,群H中的逆元.猜想e,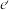 之间的关系以及
之间的关系以及 ,
, 之间的关系,并给出证明;
之间的关系,并给出证明;
③写出群S的所有子群.
 (绕中心O作120°的旋转)的作用下仍然与R重合(如图1图2所示),所以
(绕中心O作120°的旋转)的作用下仍然与R重合(如图1图2所示),所以 是R的一个对称变换,考虑到变换前后R的三个顶点间的对应关系,记
是R的一个对称变换,考虑到变换前后R的三个顶点间的对应关系,记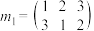 ;又如,R在
;又如,R在 (关于对称轴
(关于对称轴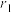 所在直线的反射)的作用下仍然与R重合(如图1图3所示),所以
所在直线的反射)的作用下仍然与R重合(如图1图3所示),所以 也是R的一个对称变换,类似地,记
也是R的一个对称变换,类似地,记 .记正三角形R的所有对称变换构成集合S.一个非空集合G对于给定的代数运算.来说作成一个群,假如同时满足:
.记正三角形R的所有对称变换构成集合S.一个非空集合G对于给定的代数运算.来说作成一个群,假如同时满足:I.
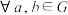 ,
, ;
;II.
 ,
, ;
;Ⅲ.
 ,
,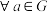 ,
, ;
;Ⅳ.
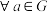 ,
,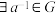 ,
,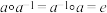 .
.对于一个群G,称Ⅲ中的e为群G的单位元,称Ⅳ中的
 为a在群G中的逆元.一个群G的一个非空子集H叫做G的一个子群,假如H对于G的代数运算
为a在群G中的逆元.一个群G的一个非空子集H叫做G的一个子群,假如H对于G的代数运算 来说作成一个群.
来说作成一个群.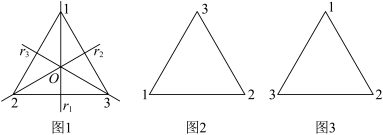
(2)同一个对称变换的符号语言表达形式不唯一,如
 .对于集合S中的元素,定义一种新运算*,规则如下:
.对于集合S中的元素,定义一种新运算*,规则如下: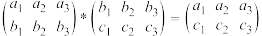 ,
, .
.①证明集合S对于给定的代数运算*来说作成一个群;
②已知H是群G的一个子群,e,
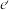 分别是G,H的单位元,
分别是G,H的单位元,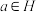 ,
, ,
, 分别是a在群G,群H中的逆元.猜想e,
分别是a在群G,群H中的逆元.猜想e,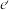 之间的关系以及
之间的关系以及 ,
, 之间的关系,并给出证明;
之间的关系,并给出证明;③写出群S的所有子群.
您最近半年使用:0次
2024-04-15更新
|
1061次组卷
|
4卷引用:安徽省芜湖市安徽师范大学附属中学2024届高三第二次模拟考试数学试题
安徽省芜湖市安徽师范大学附属中学2024届高三第二次模拟考试数学试题安徽省天域全国名校协作体2024届高三下学期联考(二模)数学试题山东省菏泽市单县第一中学2024届高三下学期3月月考数学试题(已下线)安徽省天域全国名校协作体2024届高三下学期联考(二模)数学试题变式题16-19
4 . 设集合 、
、 为正整数集
为正整数集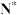 的两个子集,
的两个子集, 、
、 至少各有两个元素.对于给定的集合
至少各有两个元素.对于给定的集合 ,若存在满足如下条件的集合
,若存在满足如下条件的集合 :
:
①对于任意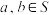 ,若
,若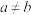 ,都有
,都有 ;②对于任意
;②对于任意 ,若
,若 ,则
,则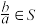 .则称集合
.则称集合 为集合
为集合 的“
的“ 集”.
集”.
(1)若集合
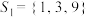 ,求
,求 的“
的“ 集”
集”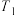 ;
;(2)若三元集
 存在“
存在“ 集”
集” ,且
,且 中恰含有4个元素,求证:
中恰含有4个元素,求证: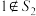 ;
;(3)若
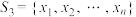 存在“
存在“ 集”,且
集”,且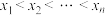 ,求
,求 的最大值.
的最大值.
您最近半年使用:0次
名校
5 . 已知集合 (
( ,
, ),若存在数阵
),若存在数阵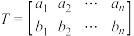 满足:
满足:
①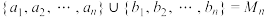 ;
;
② .
.
则称集合 为“好集合”,并称数阵
为“好集合”,并称数阵 为
为 的一个“好数阵”.
的一个“好数阵”.
(1)已知数阵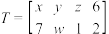 是
是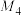 的一个“好数阵”,试写出
的一个“好数阵”,试写出 ,
, ,
, ,
, 的值;
的值;
(2)若集合 为“好集合”,证明:集合
为“好集合”,证明:集合 的“好数阵”必有偶数个;
的“好数阵”必有偶数个;
(3)判断 是否为“好集合”.若是,求出满足条件
是否为“好集合”.若是,求出满足条件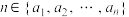 的所有“好数阵”;若不是,说明理由.
的所有“好数阵”;若不是,说明理由.
 (
( ,
, ),若存在数阵
),若存在数阵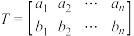 满足:
满足:①
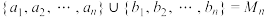 ;
;②
 .
.则称集合
 为“好集合”,并称数阵
为“好集合”,并称数阵 为
为 的一个“好数阵”.
的一个“好数阵”.(1)已知数阵
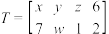 是
是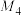 的一个“好数阵”,试写出
的一个“好数阵”,试写出 ,
, ,
, ,
, 的值;
的值;(2)若集合
 为“好集合”,证明:集合
为“好集合”,证明:集合 的“好数阵”必有偶数个;
的“好数阵”必有偶数个;(3)判断
 是否为“好集合”.若是,求出满足条件
是否为“好集合”.若是,求出满足条件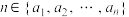 的所有“好数阵”;若不是,说明理由.
的所有“好数阵”;若不是,说明理由.
您最近半年使用:0次
2024-03-27更新
|
580次组卷
|
2卷引用:北京市丰台区2023-2024学年高三下学期综合练习(一)数学试题
名校
6 . 设A是正整数集的一个非空子集,如果对于任意 ,都有
,都有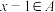 或
或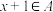 ,则称A为自邻集.记集合
,则称A为自邻集.记集合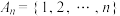
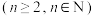 的所有子集中的自邻集的个数为
的所有子集中的自邻集的个数为 .
.
(1)直接写出 的所有自邻集;
的所有自邻集;
(2)若n为偶数且 ,求证:
,求证: 的所有含5个元素的子集中,自邻集的个数是偶数;
的所有含5个元素的子集中,自邻集的个数是偶数;
(3)若 ,求证:
,求证: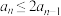 .
.
 ,都有
,都有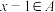 或
或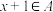 ,则称A为自邻集.记集合
,则称A为自邻集.记集合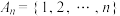
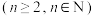 的所有子集中的自邻集的个数为
的所有子集中的自邻集的个数为 .
.(1)直接写出
 的所有自邻集;
的所有自邻集;(2)若n为偶数且
 ,求证:
,求证: 的所有含5个元素的子集中,自邻集的个数是偶数;
的所有含5个元素的子集中,自邻集的个数是偶数;(3)若
 ,求证:
,求证: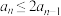 .
.
您最近半年使用:0次
名校
7 . 设 为正整数,集合
为正整数,集合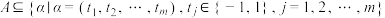 . 任取集合A中的
. 任取集合A中的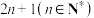 个元素(可以重复)
个元素(可以重复)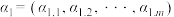 ,
,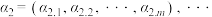 ,
, ,
,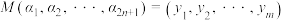 ,其中
,其中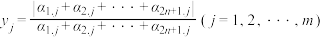 .
.
(1)若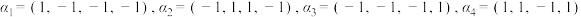 ,
, ,直接写出
,直接写出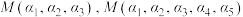 ;
;
(2)对于 ,
, ,
, ,证明:
,证明: ;
;
(3)对于某个正整数 ,若集合A满足:对于A中任意
,若集合A满足:对于A中任意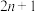 个元素
个元素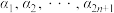 ,都有
,都有 ,则称集合A具有性质
,则称集合A具有性质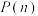 . 证明:若
. 证明:若 ,集合A具有性质
,集合A具有性质 ,则
,则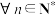 ,集合A都具有性质
,集合A都具有性质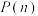 .
.
 为正整数,集合
为正整数,集合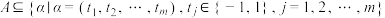 . 任取集合A中的
. 任取集合A中的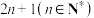 个元素(可以重复)
个元素(可以重复)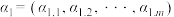 ,
,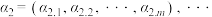 ,
, ,
,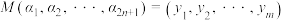 ,其中
,其中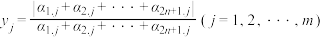 .
.(1)若
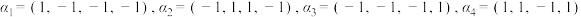 ,
, ,直接写出
,直接写出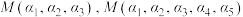 ;
;(2)对于
 ,
, ,
, ,证明:
,证明: ;
;(3)对于某个正整数
 ,若集合A满足:对于A中任意
,若集合A满足:对于A中任意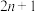 个元素
个元素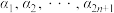 ,都有
,都有 ,则称集合A具有性质
,则称集合A具有性质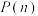 . 证明:若
. 证明:若 ,集合A具有性质
,集合A具有性质 ,则
,则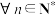 ,集合A都具有性质
,集合A都具有性质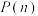 .
.
您最近半年使用:0次
名校
8 . 已知有 个连续正整数元素的有限集合
个连续正整数元素的有限集合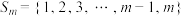 (
( ,
, ),记有序数对
),记有序数对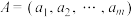 ,若对任意
,若对任意 ,
, ,
, ,
, 且
且 ,A同时满足下列条件,则称
,A同时满足下列条件,则称 为
为 元完备数对.
元完备数对.
条件①: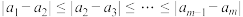 ;
;
条件②: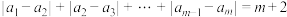 .
.
(1)试判断是否存在3元完备数对和4元完备数对,并说明理由;
(2)试证明不存在8元完备数对.
 个连续正整数元素的有限集合
个连续正整数元素的有限集合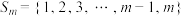 (
( ,
, ),记有序数对
),记有序数对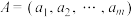 ,若对任意
,若对任意 ,
, ,
, ,
, 且
且 ,A同时满足下列条件,则称
,A同时满足下列条件,则称 为
为 元完备数对.
元完备数对.条件①:
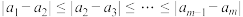 ;
;条件②:
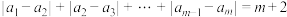 .
.(1)试判断是否存在3元完备数对和4元完备数对,并说明理由;
(2)试证明不存在8元完备数对.
您最近半年使用:0次
2024-02-23更新
|
240次组卷
|
2卷引用:北京市通州区2023-2024学年高一上学期期末质量检测数学试卷
名校
解题方法
9 . 给定正整数 ,设集合
,设集合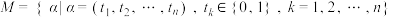 .对于集合
.对于集合 中的任意元素
中的任意元素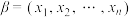 和
和 ,记
,记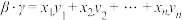 .设
.设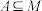 ,且集合
,且集合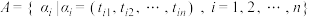 ,对于
,对于 中任意元素
中任意元素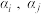 ,若
,若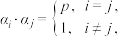 则称
则称 具有性质
具有性质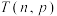 .
.
(1)判断集合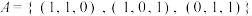 是否具有性质
是否具有性质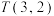 ?说明理由;
?说明理由;
(2)判断是否存在具有性质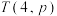 的集合
的集合 ,并加以证明.
,并加以证明.
 ,设集合
,设集合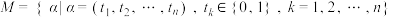 .对于集合
.对于集合 中的任意元素
中的任意元素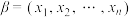 和
和 ,记
,记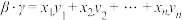 .设
.设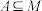 ,且集合
,且集合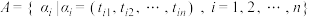 ,对于
,对于 中任意元素
中任意元素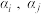 ,若
,若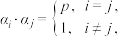 则称
则称 具有性质
具有性质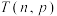 .
.(1)判断集合
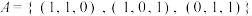 是否具有性质
是否具有性质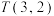 ?说明理由;
?说明理由;(2)判断是否存在具有性质
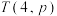 的集合
的集合 ,并加以证明.
,并加以证明.
您最近半年使用:0次
2024-01-25更新
|
266次组卷
|
4卷引用:北京市海淀区北京交通大学附属中学2023-2024学年高二上学期期中练习数学试题
北京市海淀区北京交通大学附属中学2023-2024学年高二上学期期中练习数学试题(已下线)专题04 分类讨论型【讲】【北京版】2北京市延庆区2023-2024学年高二上学期期末考试数学试卷(已下线)专题1 集合新定义题(九省联考第19题模式)练
23-24高一上·上海·期中
名校
10 . 对于正整数 ,定义
,定义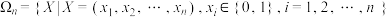 .对于任意的
.对于任意的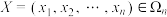 ,称
,称 为
为 的第
的第 个分量,称
个分量,称 是
是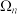 的一个“协同子集”.如果
的一个“协同子集”.如果 同时满足:①
同时满足:① 的元素个数不少于
的元素个数不少于 ;②对于任何
;②对于任何 、
、 、
、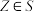 ,存在
,存在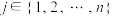 ,使得
,使得 、
、 、
、 的第
的第 个分量都是
个分量都是 .
.
(1)对于 ,若
,若 是
是 的一个恰好含有四个元素的“协同子集”,且其中两个元素是
的一个恰好含有四个元素的“协同子集”,且其中两个元素是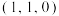 和
和 ,直接写出另外两个元素;
,直接写出另外两个元素;
(2)证明:若 是
是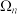 的一个“协同子集”,则
的一个“协同子集”,则 的元素个数不超过
的元素个数不超过 ;
;
(3)证明:若 是
是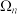 的一个“协同子集”,且
的一个“协同子集”,且 的元素个数恰好是
的元素个数恰好是 ,则存在唯一的
,则存在唯一的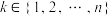 ,使得
,使得 中所有元素的第
中所有元素的第 个分量都是
个分量都是 .
.
 ,定义
,定义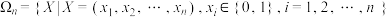 .对于任意的
.对于任意的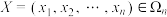 ,称
,称 为
为 的第
的第 个分量,称
个分量,称 是
是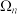 的一个“协同子集”.如果
的一个“协同子集”.如果 同时满足:①
同时满足:① 的元素个数不少于
的元素个数不少于 ;②对于任何
;②对于任何 、
、 、
、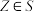 ,存在
,存在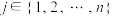 ,使得
,使得 、
、 、
、 的第
的第 个分量都是
个分量都是 .
.(1)对于
 ,若
,若 是
是 的一个恰好含有四个元素的“协同子集”,且其中两个元素是
的一个恰好含有四个元素的“协同子集”,且其中两个元素是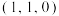 和
和 ,直接写出另外两个元素;
,直接写出另外两个元素;(2)证明:若
 是
是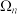 的一个“协同子集”,则
的一个“协同子集”,则 的元素个数不超过
的元素个数不超过 ;
;(3)证明:若
 是
是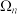 的一个“协同子集”,且
的一个“协同子集”,且 的元素个数恰好是
的元素个数恰好是 ,则存在唯一的
,则存在唯一的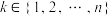 ,使得
,使得 中所有元素的第
中所有元素的第 个分量都是
个分量都是 .
.
您最近半年使用:0次



