名校
1 . 当一个非空数集 满足:如果
满足:如果 ,则
,则 ,且
,且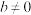 时,
时,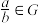 时,我们称
时,我们称 就是一个数域,以下关于数域的说法:①
就是一个数域,以下关于数域的说法:① 是任何数域的元素;②若数域
是任何数域的元素;②若数域 有非零元素,则
有非零元素,则 ;③集合
;③集合 是一个数域;④有理数集是一个数域;⑤任何一个有限数域的元素个数必为奇数,其中正确的选项是( )
是一个数域;④有理数集是一个数域;⑤任何一个有限数域的元素个数必为奇数,其中正确的选项是( )
 满足:如果
满足:如果 ,则
,则 ,且
,且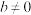 时,
时,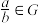 时,我们称
时,我们称 就是一个数域,以下关于数域的说法:①
就是一个数域,以下关于数域的说法:① 是任何数域的元素;②若数域
是任何数域的元素;②若数域 有非零元素,则
有非零元素,则 ;③集合
;③集合 是一个数域;④有理数集是一个数域;⑤任何一个有限数域的元素个数必为奇数,其中正确的选项是( )
是一个数域;④有理数集是一个数域;⑤任何一个有限数域的元素个数必为奇数,其中正确的选项是( )| A.①②④ | B.②③④⑤ | C.①④⑤ | D.①②④⑤ |
您最近一年使用:0次
2021-11-16更新
|
699次组卷
|
4卷引用:第1章 集合 单元综合测试卷
第1章 集合 单元综合测试卷江苏省宿迁青华中学2022-2023学年高一上学期第一次月考数学试卷B重庆市渝北中学校2021-2022学年高一上学期阶段一质量检测数学试题(已下线)第01讲 集合的概念与集合间的基本关系-【暑假自学课】2022年新高一数学暑假精品课(人教版2019必修第一册)
2 . 定义两种新运算“⊕”与“⊗”,满足如下运算法则:对任意的a,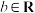 ,有
,有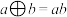 ,
,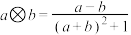 .设全集
.设全集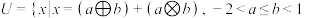 且
且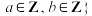 ,
, 且
且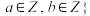 、
、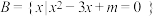 .
.
(1)求集合U和A;
(2)集合A、B是否能满足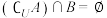 ?若能,求出实数m的取值范围;若不能,请说明理由.
?若能,求出实数m的取值范围;若不能,请说明理由.
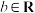 ,有
,有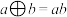 ,
,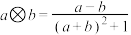 .设全集
.设全集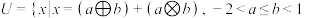 且
且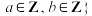 ,
, 且
且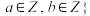 、
、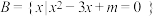 .
.(1)求集合U和A;
(2)集合A、B是否能满足
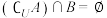 ?若能,求出实数m的取值范围;若不能,请说明理由.
?若能,求出实数m的取值范围;若不能,请说明理由.
您最近一年使用:0次
2021-11-13更新
|
2583次组卷
|
11卷引用:江苏省南通市海安高级中学2021-2022学年高一10月份段测数学试题(一)
江苏省南通市海安高级中学2021-2022学年高一10月份段测数学试题(一)辽宁省辽西2018-2019学年高一上学期第一次联合月考数学试题广东省东莞市光明中学2021-2022学年高一上学期第一次月考数学试题章节综合测试-集合与常用逻辑用语广东省东莞市东华高级中学2022-2023学年高一上学期第一次月考数学试题广东省珠海市北京师范大学珠海分校附属外国语学校2022-2023学年高一上学期9月月考数学试题湖北省十堰市丹江口市第一中学2022-2023学年高一上学期10月月考数学试题四川省阆中中学校2023-2024学年高一上学期9月教学质量检测数学试题湖北省十堰市华中师范大学附属武当中学2023-2024学年高一上学期9月月考数学试题(已下线)第一章 集合与常用逻辑用语(单元重点综合测试)-速记·巧练(人教A版2019必修第一册)(已下线)专题1 集合新定义题(九省联考第19题模式)练
名校
解题方法
3 . 若一个集合是另一个集合的子集,则称两个集合构成“鲸吞”;若两个集合有公共元素且互不为对方的子集,则称两个集合构成“蚕食”,对于集合 ,
, ,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为( )
,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为( )
 ,
, ,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为( )
,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为( )A.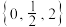 | B.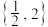 | C. | D. |
您最近一年使用:0次
2021-10-30更新
|
1014次组卷
|
7卷引用:第03讲 子集、全集、补集-【暑假自学课】(苏教版2019必修第一册)
(已下线)第03讲 子集、全集、补集-【暑假自学课】(苏教版2019必修第一册)湖北省宜昌市夷陵中学2021-2022学年高一上学期10月阶段性检测数学试题安徽省淮南第二中学2021-2022学年高二下学期博雅杯素养挑战赛数学试题2023版 湘教版(2019) 必修第一册 过关斩将 第1章 1.1.2子集和补集河南省洛阳市第一高级中学2023-2024学年高一上学期期中达标数学测评卷(B卷)(已下线)专题01 集合及集合运算求参(1)(已下线)专题01 集合及集合运算求参(1)-【寒假分层作业】(人教A版2019必修第一册)
19-20高一·全国·课后作业
名校
4 . 在整数集 中,被5除所得余数为
中,被5除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为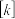 ,即
,即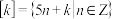 ,
,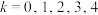 ;给出下列四个结论:①
;给出下列四个结论:① ;②
;②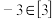 ;③
;③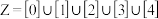 ;④“整数
;④“整数 ,
, 属于同一‘类’”的充要条件是“
属于同一‘类’”的充要条件是“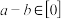 ”.其中正确的结论是
”.其中正确的结论是___________ .
 中,被5除所得余数为
中,被5除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为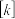 ,即
,即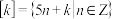 ,
,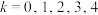 ;给出下列四个结论:①
;给出下列四个结论:① ;②
;②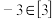 ;③
;③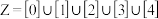 ;④“整数
;④“整数 ,
, 属于同一‘类’”的充要条件是“
属于同一‘类’”的充要条件是“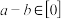 ”.其中正确的结论是
”.其中正确的结论是
您最近一年使用:0次
2021-10-27更新
|
492次组卷
|
10卷引用:第2章 常用逻辑用语 单元综合检测(单元培优)-2021-2022学年高一数学课后培优练(苏教版2019必修第一册)
(已下线)第2章 常用逻辑用语 单元综合检测(单元培优)-2021-2022学年高一数学课后培优练(苏教版2019必修第一册)(已下线)第02练 常用逻辑用语-2022年【寒假分层作业】高一数学(苏教版2019必修第一册)(已下线)第06讲 充分条件、必要条件、充要条件-【暑假自学课】(苏教版2019必修第一册)(已下线)专题08集合单元复习--2020年初升高数学无忧衔接(沪教版)(已下线)专题21+期中复习-2020-2021学年新教材高一数学秋季辅导讲义(沪教2020)知识点02 充分条件、必要条件、充要条件-【提升专练】2021-2022学年高一数学新教材同步学案+课时对点练(苏教版2019必修第一册)广东省南海区佛山市超盈实验中学、佛山市美术实验中学2021-2022学年高一上学期第一次学科素养监测(月考)数学试题(已下线)专题01 集合与逻辑(讲义)-2(已下线)高一上学期期中考试填空题压轴题50题专练-举一反三系列上海市朱家角中学2023-2024学年高一上学期第一阶段质量检测数学试题
5 . 由无理数引发的数学危机一直延续到19世纪直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集 划分为两个非空子集
划分为两个非空子集 与
与 ,且满足
,且满足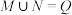 ,
,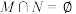 ,
, 中的每一个元素都小于
中的每一个元素都小于 中的每一个元素,则称
中的每一个元素,则称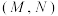 为戴德金分割.试判断下列选项中,可能成立的是
为戴德金分割.试判断下列选项中,可能成立的是___________ .
①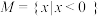 ,
,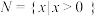 是一个戴德金分割;
是一个戴德金分割;
② 没有最大元素,
没有最大元素,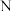 有一个最小元素;
有一个最小元素;
③ 有一个最大元素,
有一个最大元素,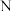 有一个最小元素;
有一个最小元素;
④ 没有最大元素,
没有最大元素,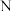 没有最小元素;
没有最小元素;
 划分为两个非空子集
划分为两个非空子集 与
与 ,且满足
,且满足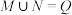 ,
,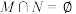 ,
, 中的每一个元素都小于
中的每一个元素都小于 中的每一个元素,则称
中的每一个元素,则称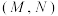 为戴德金分割.试判断下列选项中,可能成立的是
为戴德金分割.试判断下列选项中,可能成立的是①
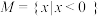 ,
,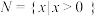 是一个戴德金分割;
是一个戴德金分割;②
 没有最大元素,
没有最大元素,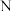 有一个最小元素;
有一个最小元素;③
 有一个最大元素,
有一个最大元素,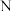 有一个最小元素;
有一个最小元素;④
 没有最大元素,
没有最大元素,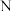 没有最小元素;
没有最小元素;
您最近一年使用:0次
2021-10-22更新
|
777次组卷
|
5卷引用:1.3 交集、并集(2)
(已下线)1.3 交集、并集(2)北京市东北师范大学附属中学朝阳学校2021-2022高一第一次质量监测及反馈试题北京市通州区运河中学2021-2022学年高一10月诊断数学试题(已下线)数学与数学家(已下线)专题11 集合的基本运算(交集与并集)-2022年暑假初三升高一数学衔接知识自学讲义(人教A版2019)
名校
6 . 设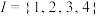 ,
, 与
与 是
是 的子集,若
的子集,若 ,则称
,则称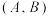 为一个“理想配集”.规定
为一个“理想配集”.规定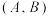 与
与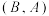 是两个不同的“理想配集”,那么符合此条件的“理想配集”的个数是( )
是两个不同的“理想配集”,那么符合此条件的“理想配集”的个数是( )
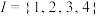 ,
, 与
与 是
是 的子集,若
的子集,若 ,则称
,则称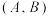 为一个“理想配集”.规定
为一个“理想配集”.规定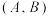 与
与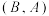 是两个不同的“理想配集”,那么符合此条件的“理想配集”的个数是( )
是两个不同的“理想配集”,那么符合此条件的“理想配集”的个数是( )| A.4 | B.6 | C.8 | D.9 |
您最近一年使用:0次
2021-10-21更新
|
607次组卷
|
6卷引用:江苏省连云港市海州高级中学2021--2022学年高一上学期9月月考数学试题
名校
7 . 定义非空集合A的真子集的真子集为A的“孙集”,则集合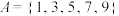 的“孙集”的个数为
的“孙集”的个数为___________ .
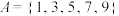 的“孙集”的个数为
的“孙集”的个数为
您最近一年使用:0次
2021-10-21更新
|
292次组卷
|
4卷引用:第01练 集合-2022年【寒假分层作业】高一数学(苏教版2019必修第一册)
(已下线)第01练 集合-2022年【寒假分层作业】高一数学(苏教版2019必修第一册)河北省石家庄市四中2021-2022学年高一上学期第一次月考(10月)数学试题苏教版(2019) 必修第一册 过关检测 第1章 专题 集合中的综合问题1.2 集合的基本关系—2021-2022学年高一上学期数学北师大版2019必修第一册
名校
8 . 在整数集 中,被
中,被 除所得余数为
除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为 ,即
,即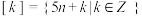 ,
,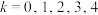 ,给出如下四个结论,正确结论为( )
,给出如下四个结论,正确结论为( )
 中,被
中,被 除所得余数为
除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为 ,即
,即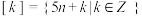 ,
,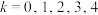 ,给出如下四个结论,正确结论为( )
,给出如下四个结论,正确结论为( )A.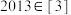 |
B.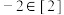 |
C.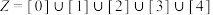 |
D.整数 属于同一“类”的充要条件是“ 属于同一“类”的充要条件是“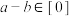 ” ” |
您最近一年使用:0次
2021-10-20更新
|
762次组卷
|
5卷引用:第2章 常用逻辑用语 单元综合检测(难点)
第2章 常用逻辑用语 单元综合检测(难点)辽宁省大连育明高级中学2021-2022学年高一上学期10月月考数学试题广西钦州市第二中学2021-2022学年高一上学期期中考试数学试题广东省汕尾华大实验学校2022-2023学年高一上学期9月月考数学试题(已下线)第一章 集合与常用逻辑用语单元测试(巅峰版)-【冲刺满分】
9 . 对任意 ,定义
,定义 .例如,若
.例如,若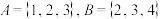 ,则
,则 ,下列命题中为真命题的是( )
,下列命题中为真命题的是( )
 ,定义
,定义 .例如,若
.例如,若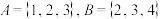 ,则
,则 ,下列命题中为真命题的是( )
,下列命题中为真命题的是( )A.若 且 且 ,则 ,则 | B.若 且 且 ,则 ,则 |
C.若 且 且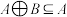 ,则 ,则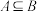 | D.若 ,则 ,则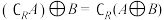 |
您最近一年使用:0次
2021-10-07更新
|
1331次组卷
|
13卷引用:专题1.3 交集、并集(2)-【帮课堂】-(苏教版2019必修第一册)
(已下线)专题1.3 交集、并集(2)-【帮课堂】-(苏教版2019必修第一册)四川外国语大学附属外国语学校(重庆外国语学校)2021-2022学年高一上学期9月检测数学试题四川外国语大学附属外国语学校(重庆外国语学校)2021-2022学年高一上学期9月月考数学试题江西省进贤县第一中学2021-2022学年高一上学期第一次月考数学试题第一章 集合与常用逻辑用语(A卷·基础通关练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教B版2019必修第一册)安徽省蚌埠市2022-2023学年高一上学期期末学业水平监测数学试题(已下线)专题1.8 集合与常用逻辑用语全章综合测试卷(提高篇)-举一反三系列(已下线)第1章 集合与常用逻辑用语(基础、典型、新文化、压轴)分类专项训练-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)安徽省合肥市第十中学2023-2024学年高一上学期10月月考数学试题(已下线)专题02 高一上期中真题精选-期中考点大串讲(人教A版2019必修第一册)(已下线)第一章 集合与常用逻辑用语(知识归纳+7类题型突破)-速记·巧练(人教A版2019必修第一册)(已下线)高一上学期期末考试选择题压轴题50题专练-举一反三系列(已下线)高一上学期期末数学试卷(提高篇)-举一反三系列
名校
解题方法
10 . 若一个集合是另一个集合的子集,则称两个集合构成“鲸吞”;若两个集合有公共元素,且互不为对方子集,则称两个集合构成“蚕食”,对于集合 ,
, ,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为
,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为_____ .
 ,
, ,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为
,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为
您最近一年使用:0次
2021-10-04更新
|
2605次组卷
|
26卷引用:江苏省徐州市沛县2022-2023学年高一上学期第一次学情调研数学试题
江苏省徐州市沛县2022-2023学年高一上学期第一次学情调研数学试题山东省烟台市2020-2021学年高一上学期期中数学试题(已下线)专题1.3 集合间的基本关系-重难点题型精讲-2021-2022学年高一数学举一反三系列(人教A版2019必修第一册)河南省林州市第一中学2021-2022学年高一上学期开学检测(普通班)数学试题(已下线)专题1.3 集合的基本关系-重难点题型精讲-2021-2022学年高一数学举一反三系列(北师大版2019必修第一册)(已下线)专题1.3 集合的基本关系-重难点题型精讲-2021-2022学年高一数学举一反三系列(人教B版2019必修第一册)(已下线)第1章集合与常用逻辑用语专练1 集合-2022届高三数学一轮复习湖北省武汉市第十一中学2021-2022学年高一上学期第一次月考数学试题湖北省武汉市吴家山中学2021-2022学年高一上学期第一次月考数学试题河南省漯河市高级中学2021-2022学年高一上学期10月月考数学试题新疆喀什第六中学2021-2022学年高一12月月考数学试题湖南省邵阳市第二中学2021-2022学年高一上学期第一次月考数学试题(已下线)1.1 集合(精讲)-【一隅三反】2023年高考数学一轮复习(提升版)(新高考地区专用)北师大版(2019) 必修第一册 名校名师卷 第一单元 集合2023版 苏教版(2019) 必修第一册 名师精选卷 第一单元 集合2023版 湘教版(2019) 必修第一册 名师精选卷 第一单元 集合湖北省麻城市博达学校2022-2023学年高一上学期9月月考数学试题福建省福州市长乐第一中学2022-2023学年高一上学期第一次月考数学试题上海市进才中学2022-2023学年高一上学期10月月考数学试题沪教版(2020) 必修第一册 精准辅导 第1章 1.1(4) 集合的运算河南省禹州市第一高级中学2022-2023学年高一上学期第一次月考数学试题(已下线)专题01 集合-2湖北省武汉市第二中学2023-2024学年高一上学期第一次月考数学试题广东省佛山市顺德区杏坛中学2023-2024学年高一上学期10月月考数学试题湖北省武汉市第二中学2023-2024学年高一上学期10月月考数学试题陕西省西安市第八十五中学2023-2024学年高一上学期第一次摸底考试数学试题



