1 . 若函数 的图象上的两个不同点处的切线互相重合,则称该切线为函数
的图象上的两个不同点处的切线互相重合,则称该切线为函数 的图象的“自公切线”,称这两点为函数
的图象的“自公切线”,称这两点为函数 的图象的一对“同切点”.
的图象的一对“同切点”.
(1)分别判断函数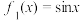 与
与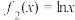 的图象是否存在“自公切线”,并说明理由;
的图象是否存在“自公切线”,并说明理由;
(2)若 ,求证:函数
,求证:函数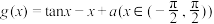 有唯一零点且该函数的图象不存在“自公切线”;
有唯一零点且该函数的图象不存在“自公切线”;
(3)设 ,
,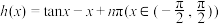 的零点为
的零点为 ,
, ,求证:“存在
,求证:“存在 ,使得点
,使得点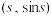 与
与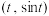 是函数
是函数 的图象的一对‘同切点’”的充要条件是“
的图象的一对‘同切点’”的充要条件是“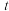 是数列
是数列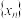 中的项”.
中的项”.
 的图象上的两个不同点处的切线互相重合,则称该切线为函数
的图象上的两个不同点处的切线互相重合,则称该切线为函数 的图象的“自公切线”,称这两点为函数
的图象的“自公切线”,称这两点为函数 的图象的一对“同切点”.
的图象的一对“同切点”.(1)分别判断函数
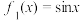 与
与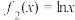 的图象是否存在“自公切线”,并说明理由;
的图象是否存在“自公切线”,并说明理由;(2)若
 ,求证:函数
,求证:函数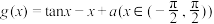 有唯一零点且该函数的图象不存在“自公切线”;
有唯一零点且该函数的图象不存在“自公切线”;(3)设
 ,
,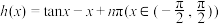 的零点为
的零点为 ,
, ,求证:“存在
,求证:“存在 ,使得点
,使得点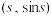 与
与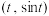 是函数
是函数 的图象的一对‘同切点’”的充要条件是“
的图象的一对‘同切点’”的充要条件是“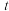 是数列
是数列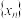 中的项”.
中的项”.
您最近一年使用:0次
2 . 设X,Y为任意集合,映射 .定义:对任意
.定义:对任意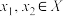 ,若
,若 ,则
,则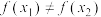 ,此时的
,此时的 为单射.
为单射.
(1)试在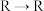 上给出一个非单射的映射;
上给出一个非单射的映射;
(2)证明: 是单射的充分必要条件是:给定任意其他集合
是单射的充分必要条件是:给定任意其他集合 与映射
与映射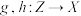 ,若对任意
,若对任意 ,有
,有 ,则
,则 ;
;
(3)证明: 是单射的充分必要条件是:存在映射
是单射的充分必要条件是:存在映射 ,使对任意
,使对任意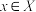 ,有
,有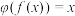 .
.
 .定义:对任意
.定义:对任意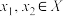 ,若
,若 ,则
,则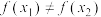 ,此时的
,此时的 为单射.
为单射.(1)试在
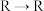 上给出一个非单射的映射;
上给出一个非单射的映射;(2)证明:
 是单射的充分必要条件是:给定任意其他集合
是单射的充分必要条件是:给定任意其他集合 与映射
与映射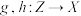 ,若对任意
,若对任意 ,有
,有 ,则
,则 ;
;(3)证明:
 是单射的充分必要条件是:存在映射
是单射的充分必要条件是:存在映射 ,使对任意
,使对任意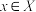 ,有
,有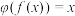 .
.
您最近一年使用:0次
3 . 已知集合 中含有三个元素
中含有三个元素 ,同时满足①
,同时满足①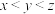 ;②
;②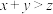 ;③
;③ 为偶数,那么称集合
为偶数,那么称集合 具有性质
具有性质 .已知集合
.已知集合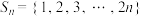
 ,对于集合
,对于集合 的非空子集
的非空子集 ,若
,若 中存在三个互不相同的元素
中存在三个互不相同的元素 ,使得
,使得 均属于
均属于 ,则称集合
,则称集合 是集合
是集合 的“期待子集”.
的“期待子集”.
(1)试判断集合 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(2)若集合 具有性质
具有性质 ,证明:集合
,证明:集合 是集合
是集合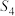 的“期待子集”;
的“期待子集”;
(3)证明:集合 具有性质
具有性质 的充要条件是集合
的充要条件是集合 是集合
是集合 的“期待子集”.
的“期待子集”.
 中含有三个元素
中含有三个元素 ,同时满足①
,同时满足①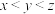 ;②
;②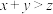 ;③
;③ 为偶数,那么称集合
为偶数,那么称集合 具有性质
具有性质 .已知集合
.已知集合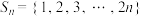
 ,对于集合
,对于集合 的非空子集
的非空子集 ,若
,若 中存在三个互不相同的元素
中存在三个互不相同的元素 ,使得
,使得 均属于
均属于 ,则称集合
,则称集合 是集合
是集合 的“期待子集”.
的“期待子集”.(1)试判断集合
 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;(2)若集合
 具有性质
具有性质 ,证明:集合
,证明:集合 是集合
是集合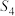 的“期待子集”;
的“期待子集”;(3)证明:集合
 具有性质
具有性质 的充要条件是集合
的充要条件是集合 是集合
是集合 的“期待子集”.
的“期待子集”.
您最近一年使用:0次
2024-02-21更新
|
2559次组卷
|
9卷引用:广东省东莞中学、广州二中、惠州一中、深圳实验、珠海一中、中山纪念中学2024届高三第四次六校联考数学试题
广东省东莞中学、广州二中、惠州一中、深圳实验、珠海一中、中山纪念中学2024届高三第四次六校联考数学试题(已下线)专题1 集合新定义题(九省联考第19题模式)讲(已下线)专题1 集合新定义题(九省联考第19题模式)练安徽省芜湖市安徽师大附中2023-2024学年高二下学期3月测试数学试题(已下线)拔高点突破01 集合背景下的新定义压轴解答题(四大题型)福建省宁德市福鼎市第一中学2024-2025学年高三上学期第一次考试数学试题江苏省木渎高级中学2024-2025学年高一上学期十月调研测试数学试题河南省郑州市第一中学2024-2025学年高一上学期第一次模拟测试数学试题江苏省苏州实验中学2024-2025学年高一上学期10月月考数学试题
名校
解题方法
4 . 若数列 满足:
满足: ,且
,且 ,则称
,则称 为一个
为一个 数列.对于一个
数列.对于一个 数列
数列 ,若数列
,若数列 满足:
满足: ,且
,且 ,则称
,则称 为
为 的伴随数列.
的伴随数列.
(1)若 数列
数列 中,
中,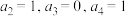 ,写出其伴随数列
,写出其伴随数列 中
中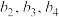 的值;
的值;
(2)若 为一个
为一个 数列,
数列, 为
为 的伴随数列
的伴随数列
①证明:“ 为常数列”是“
为常数列”是“ 为等比数列的充要条件;
为等比数列的充要条件;
②求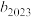 的最大值.
的最大值.
 满足:
满足: ,且
,且 ,则称
,则称 为一个
为一个 数列.对于一个
数列.对于一个 数列
数列 ,若数列
,若数列 满足:
满足: ,且
,且 ,则称
,则称 为
为 的伴随数列.
的伴随数列.(1)若
 数列
数列 中,
中,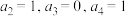 ,写出其伴随数列
,写出其伴随数列 中
中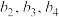 的值;
的值;(2)若
 为一个
为一个 数列,
数列, 为
为 的伴随数列
的伴随数列①证明:“
 为常数列”是“
为常数列”是“ 为等比数列的充要条件;
为等比数列的充要条件;②求
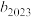 的最大值.
的最大值.
您最近一年使用:0次
2023-12-11更新
|
1485次组卷
|
2卷引用:广东省2024届高三数学新改革适应性训练一(九省联考题型)



