名校
1 . 若 ,则
,则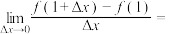
______ .
 ,则
,则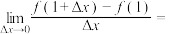
您最近半年使用:0次
2 . 已知函数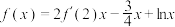 ,则
,则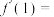
______ .
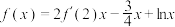 ,则
,则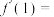
您最近半年使用:0次
3 . 下列函数的导数运算正确的是( )
A. | B.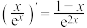 |
C. | D.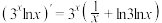 |
您最近半年使用:0次
4 . 已知 ,则
,则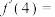 ( )
( )
 ,则
,则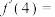 ( )
( )A. | B.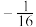 | C.16 | D.-16 |
您最近半年使用:0次
5 . 求曲线 在点
在点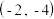 处的切线方程
处的切线方程_______________ .
 在点
在点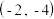 处的切线方程
处的切线方程
您最近半年使用:0次
名校
解题方法
6 . 已知函数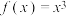 ,则
,则 ( )
( )
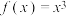 ,则
,则 ( )
( )| A.1 | B.2 | C.3 | D.4 |
您最近半年使用:0次
名校
7 . 已知函数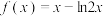 .求
.求 在
在 处的切线方程
处的切线方程__________ .
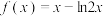 .求
.求 在
在 处的切线方程
处的切线方程
您最近半年使用:0次
8 . 曲线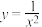 在点
在点 处的切线方程为
处的切线方程为______ .
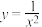 在点
在点 处的切线方程为
处的切线方程为
您最近半年使用:0次
9 . 已知曲线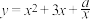 在
在 处的切线与直线
处的切线与直线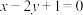 垂直,则
垂直,则 ( )
( )
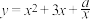 在
在 处的切线与直线
处的切线与直线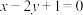 垂直,则
垂直,则 ( )
( )| A.3 | B. | C.7 | D.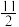 |
您最近半年使用:0次
名校
10 . 设函数 ,则
,则
__________ .
 ,则
,则
您最近半年使用:0次



