名校
解题方法
1 . 在 中,设内角A,B,C所对的边分别为
中,设内角A,B,C所对的边分别为 .
.
(1) ,
, ,是否存在正整数
,是否存在正整数 ,使得
,使得 ,且
,且 为钝角三角形?若存在,求出
为钝角三角形?若存在,求出 ;若不存在,说明理由.
;若不存在,说明理由.
(2)若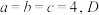 为
为 的中点,E,F分别在线段
的中点,E,F分别在线段 上,且
上,且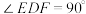 ,
,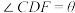
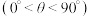 ,求
,求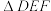 面积
面积 的最小值及此时对应的
的最小值及此时对应的 的值.
的值.
 中,设内角A,B,C所对的边分别为
中,设内角A,B,C所对的边分别为 .
.(1)
 ,
, ,是否存在正整数
,是否存在正整数 ,使得
,使得 ,且
,且 为钝角三角形?若存在,求出
为钝角三角形?若存在,求出 ;若不存在,说明理由.
;若不存在,说明理由.(2)若
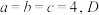 为
为 的中点,E,F分别在线段
的中点,E,F分别在线段 上,且
上,且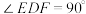 ,
,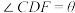
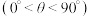 ,求
,求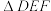 面积
面积 的最小值及此时对应的
的最小值及此时对应的 的值.
的值.
您最近一年使用:0次
2024-10-19更新
|
538次组卷
|
2卷引用:山东省聊城市水城中学2024-2025学年高三上学期第一次备考监测联考(10月)数学试题
名校
2 . 已知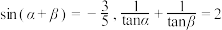 ,则
,则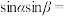 ( )
( )
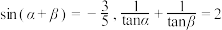 ,则
,则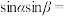 ( )
( )A.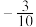 | B. | C. | D. |
您最近一年使用:0次
2024-09-07更新
|
1895次组卷
|
6卷引用:山东省聊城第一中学2025届高三上学期第一次月考数学试题
名校
解题方法
3 . 在 中,角
中,角 的对边分别是
的对边分别是 ,已知
,已知 .
.
(1)求角 ;
;
(2)若点 在边
在边 上,且
上,且 ,求
,求 面积的最大值.
面积的最大值.
 中,角
中,角 的对边分别是
的对边分别是 ,已知
,已知 .
.(1)求角
 ;
;(2)若点
 在边
在边 上,且
上,且 ,求
,求 面积的最大值.
面积的最大值.
您最近一年使用:0次
2024-09-02更新
|
2068次组卷
|
11卷引用:山东省聊城市2021-2022学年高三上学期期末数学试题
山东省聊城市2021-2022学年高三上学期期末数学试题山东省济南市2021-2022学年高三上学期期末数学试题浙江省湖州市2021-2022学年高二下学期期末数学试题江苏省南京师范大学附属中学2022-2023学年高三上学期期初阶段考试数学试题河北省沧州市普通高中2023届高三上学期摸底考数学试题江苏省南京师范大学附属中学2024届高三上学期零模模拟数学试卷江苏省赣榆高级中学2022-2023学年高三下学期4月联考调研数学试题湖北省黄冈市浠水县第一中学2024-2025学年高二上学期9月月考数学试题黑龙江省鹤岗市第一中学2023-2024学年高二上学期9月考试数学试题贵州省毕节市织金育才学校2024-2025学年高二上学期9月月考数学试卷黑龙江省哈尔滨市第九中学校2024-2025学年高三上学期期中考试数学试卷
解题方法
4 . 已知 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,若
,若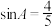 ,
,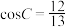 ,
, ,则
,则 ( )
( )
 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,若
,若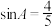 ,
,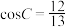 ,
, ,则
,则 ( )
( )A.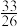 | B.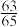 | C.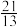 | D.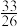 或 或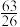 |
您最近一年使用:0次
解题方法
5 . 在 中,已知角
中,已知角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,
,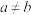 ,且
,且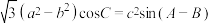 ,则
,则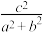 的取值范围为
的取值范围为______ .
 中,已知角
中,已知角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,
,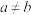 ,且
,且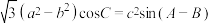 ,则
,则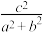 的取值范围为
的取值范围为
您最近一年使用:0次
解题方法
6 . 记 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若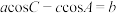 ,则
,则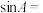 ( )
( )
 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若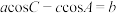 ,则
,则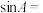 ( )
( )A. | B. | C. | D.1 |
您最近一年使用:0次
2024-07-29更新
|
696次组卷
|
4卷引用:山东省聊城市莘县第一中学2025届高三上学期开学考试数学试题
解题方法
7 . 在 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且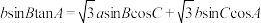 .
.
(1)求 ;
;
(2)若 在边
在边 上,且
上,且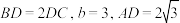 ,求
,求 的周长.
的周长.
 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且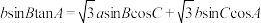 .
.(1)求
 ;
;(2)若
 在边
在边 上,且
上,且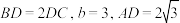 ,求
,求 的周长.
的周长.
您最近一年使用:0次
2024-05-16更新
|
1651次组卷
|
3卷引用:2024届山东省聊城市高三三模数学试题
名校
解题方法
8 . 在 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知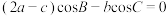 .
.
(1)求 ;
;
(2)已知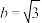 ,求
,求 的最大值.
的最大值.
 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知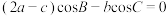 .
.(1)求
 ;
;(2)已知
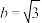 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
2024-05-16更新
|
2422次组卷
|
3卷引用:山东省聊城第一中学2025届高三上学期第一次月考数学试题
名校
解题方法
9 . 在梯形 中,
中,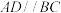 ,设
,设 ,
,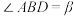 ,已知
,已知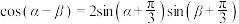 .
.
(1)求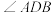 ;
;
(2)若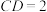 ,
, ,
,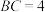 ,求
,求 .
.
 中,
中,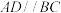 ,设
,设 ,
,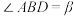 ,已知
,已知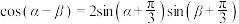 .
.(1)求
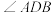 ;
;(2)若
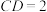 ,
, ,
,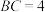 ,求
,求 .
.
您最近一年使用:0次
2024-03-14更新
|
1333次组卷
|
4卷引用:山东省聊城市2024届高考模拟数学试题(一)
山东省聊城市2024届高考模拟数学试题(一)(已下线)6.4.3.2?正弦定理15种常考题型归类(2)-高频考点通关与解题策略(人教A版2019必修第二册)广东省东莞市东莞中学松山湖学校2023-2024学年高一下学期第一次段考数学试题(已下线)6.4.3.2 正弦定理——课后作业(提升版)
解题方法
10 . 已知 ,
,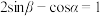 ,
,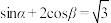 ,则
,则 ( )
( )
 ,
,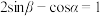 ,
,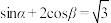 ,则
,则 ( )
( )A. | B. | C. | D. |
您最近一年使用:0次



