1 . 球的性质
(1)球面上所有的点到球心的距离都__________ ,等于球的__________ .
(2)用任何一个平面去截球面,得到的截面都是圆,其中过球心的平面截球面得到的圆的半径最大,等于球的__________ .
(1)球面上所有的点到球心的距离都
(2)用任何一个平面去截球面,得到的截面都是圆,其中过球心的平面截球面得到的圆的半径最大,等于球的
您最近一年使用:0次
2 . 圆柱、圆锥、圆台、球
| 旋转体 | 定义及相关概念 | 图形 | 表示 |
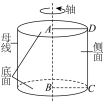
| 圆柱 | 如图,将矩形 (及其内部)绕其 (及其内部)绕其 |
| 圆柱可以用表示它的轴的字母来表示,如图中的圆柱记作 |
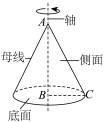
| 圆锥 | 如图,将直角三角形 (及其内部)绕其 (及其内部)绕其 |
| 圆锥也用表示它的轴的字母来表示,如图中的圆锥记作 |
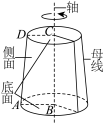
| 圆台 | 如图,将直角梯形 (及其内部)绕其垂直于底边的 (及其内部)绕其垂直于底边的 |
| 圆台也用表示它的轴的字母来表示,如图中的圆台记作 |
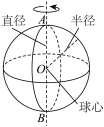
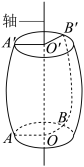
| 球 | 如图,将圆心为O的半圆(及其内部)绕其 |
| 球常用表示球心的字母来表示,如图中的球记作 |
您最近一年使用:0次
3 . 锥体、台体、柱体的高
(1)锥体(棱锥、圆锥)的__________ 到__________ 的__________ 称为锥体的高.
(2)台体(棱台、圆台)或柱体(棱柱、圆柱)的__________ 之间的__________ 称为台体或柱体的高
(1)锥体(棱锥、圆锥)的
(2)台体(棱台、圆台)或柱体(棱柱、圆柱)的
您最近一年使用:0次
4 . 观察下面的长方体,它的每个面是什么样的多边形?不同的面之间有什么位置关系?
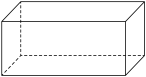
您最近一年使用:0次
5 .
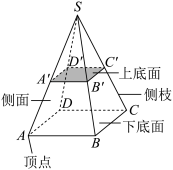
| 多面体 | 棱锥 | 棱台 |
| 定义 | 有一个面是 | 过棱锥任一侧棱上不与侧棱端点重合的一点,作一个与底面平行的平面去截棱锥,截面和原棱锥底面之间的这部分几何体叫作棱台 |
| 图形及表示 |
 |
 |
| 相关 概念 | 具有同一个公共顶点的三角形面叫作棱锥的 | |
| 特殊 情形 | 如果棱锥的底面是正多边形,将底面水平放置后,它的顶点又在过正多边形中心的铅垂线上,则这样的棱锥称为正棱锥 | 正棱台:由正棱锥截得的棱台 |
您最近一年使用:0次
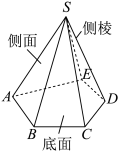
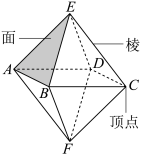
6 . 图中的多面体具有怎样的特点?
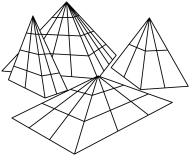
您最近一年使用:0次
7 . 几个特殊的棱柱
(1)直棱柱:侧面都是__________ 的棱柱;
(2)正棱柱:底面是__________ 的直棱柱;
(3)长方体:底面和侧面都是的__________ 棱柱;
(4)正方体:所有棱长__________ 的长方体;
(5)平行六面体:两个底面是__________ 的棱柱.
(1)直棱柱:侧面都是
(2)正棱柱:底面是
(3)长方体:底面和侧面都是的
(4)正方体:所有棱长
(5)平行六面体:两个底面是
您最近一年使用:0次
23-24高一下·全国·课前预习
8 . 多面体、旋转体
类别 | 多面体 | 旋转体 |
定义 | 一般地,由若干个 | 一条平面曲线(包括直线)绕它所在平面内的 |
图形 |
|
|
相关概念 | 面:围成多面体的各个 棱:两个面的 顶点:棱与棱的公共点 | 轴:形成旋转体所绕的定直线 |
您最近一年使用:0次
23-24高一下·全国·课前预习
9 . 几个特殊的棱柱
(1)直棱柱:________ 的棱柱叫做直棱柱(如图①③);
(2)斜棱柱:________ 的棱柱叫做斜棱柱(如图②④);
(3)正棱柱:底面是正多边形的________ 叫做正棱柱(如图③);
(4)平行六面体:底面是________ 的四棱柱也叫做平行六面体(如图④).
(1)直棱柱:
(2)斜棱柱:
(3)正棱柱:底面是正多边形的
(4)平行六面体:底面是

您最近一年使用:0次