解题方法
1 . 如图是一座类似于上海卢浦大桥的圆拱桥示意图,该圆弧拱跨度 为
为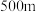 ,圆拱的最高点
,圆拱的最高点 离水面
离水面 的高度为
的高度为 ,桥面
,桥面 离水面
离水面 的高度为
的高度为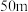 .
.
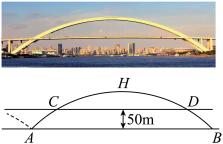
(1)建立适当的平面直角坐标系,求圆拱所在圆的方程;
(2)求桥面在圆拱内部分 的长度.(结果精确到
的长度.(结果精确到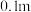 )
)
 为
为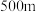 ,圆拱的最高点
,圆拱的最高点 离水面
离水面 的高度为
的高度为 ,桥面
,桥面 离水面
离水面 的高度为
的高度为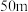 .
.
(1)建立适当的平面直角坐标系,求圆拱所在圆的方程;
(2)求桥面在圆拱内部分
 的长度.(结果精确到
的长度.(结果精确到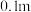 )
)
您最近一年使用:0次
2023-06-20更新
|
955次组卷
|
7卷引用:通关练11 圆的方程大题10考点精练(47题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)
(已下线)通关练11 圆的方程大题10考点精练(47题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)上海市静安区2022-2023学年高二下学期期末数学试题第二章 直线和圆的方程 (练基础)(已下线)第08讲 2.4.2圆的一般方程(10 类热点题型讲练)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第一册)(已下线)专题2.9 直线与圆的方程大题专项训练(30道)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)2.1 圆的方程(八大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)(已下线)专题17 直线与圆的位置关系9种常见考法归类- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教B版2019选择性必修第一册)
2 . 如图,一隧道内设双行线公路,其截面由一个长方形(长、宽分别为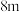 、
、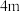 )和圆弧构成,截面总高度为
)和圆弧构成,截面总高度为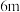 ,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有
,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有 米,已知行车道总宽度
米,已知行车道总宽度 .
.
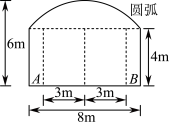
(1)试建立恰当的坐标系,求出圆弧所在圆的一般方程;
(2)车辆通过隧道的限制高度为多少米?
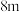 、
、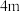 )和圆弧构成,截面总高度为
)和圆弧构成,截面总高度为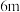 ,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有
,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有 米,已知行车道总宽度
米,已知行车道总宽度 .
.
(1)试建立恰当的坐标系,求出圆弧所在圆的一般方程;
(2)车辆通过隧道的限制高度为多少米?
您最近一年使用:0次
2023-06-17更新
|
424次组卷
|
7卷引用:2.5.1 直线与圆的位置关系 精练(10大题型)-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)
(已下线)2.5.1 直线与圆的位置关系 精练(10大题型)-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)(已下线)通关练11 圆的方程大题10考点精练(47题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)山西省晋中市2022-2023学年高二上学期期末数学试题(已下线)第17讲 直线与圆的位置关系8种常见考法归类(2)(已下线)第09讲 2.5.1直线与圆的位置关系(2)内蒙古自治区优质高中联考2023-2024学年高二上学期11月期中数学试题(已下线)第02讲 2.4圆的方程+2.5直线与圆,圆与圆的位置关系(4)
解题方法
3 . 已知 的内角A、B、C所对的边分别为a,b、c,
的内角A、B、C所对的边分别为a,b、c, 的面积为S,若
的面积为S,若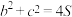 .
.
(1)求证: ;
;
(2)若 ,P为
,P为 内一点,且
内一点,且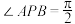 ,求
,求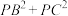 的取值范围.
的取值范围.
 的内角A、B、C所对的边分别为a,b、c,
的内角A、B、C所对的边分别为a,b、c, 的面积为S,若
的面积为S,若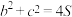 .
.(1)求证:
 ;
;(2)若
 ,P为
,P为 内一点,且
内一点,且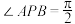 ,求
,求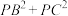 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
4 . 如图,某海面上有O,A,B三个小岛(面积大小忽略不计),A岛在O岛的北偏东45°方向距O岛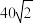 千米处,B岛在O岛的正东方向距O岛20千米处.以O为坐标原点,O的正东方向为x轴的正方向,1千米为一个单位长度,建立平面直角坐标系.圆C经过O,A,B三点.
千米处,B岛在O岛的正东方向距O岛20千米处.以O为坐标原点,O的正东方向为x轴的正方向,1千米为一个单位长度,建立平面直角坐标系.圆C经过O,A,B三点.
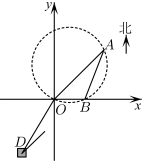
(1)求圆C的方程;
(2)若圆C区域内有未知暗礁,现有一船D在O岛的南偏西30°方向距O岛40千米处,正沿着北偏东45°方向行驶,若不改变方向,试问该船有没有触礁的危险?
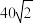 千米处,B岛在O岛的正东方向距O岛20千米处.以O为坐标原点,O的正东方向为x轴的正方向,1千米为一个单位长度,建立平面直角坐标系.圆C经过O,A,B三点.
千米处,B岛在O岛的正东方向距O岛20千米处.以O为坐标原点,O的正东方向为x轴的正方向,1千米为一个单位长度,建立平面直角坐标系.圆C经过O,A,B三点.
(1)求圆C的方程;
(2)若圆C区域内有未知暗礁,现有一船D在O岛的南偏西30°方向距O岛40千米处,正沿着北偏东45°方向行驶,若不改变方向,试问该船有没有触礁的危险?
您最近一年使用:0次
2022-08-31更新
|
1702次组卷
|
28卷引用:【新教材精创】2.5.1+直线与圆的位置关系+B提高练-人教A版高中数学选择性必修第一册
(已下线)【新教材精创】2.5.1+直线与圆的位置关系+B提高练-人教A版高中数学选择性必修第一册(已下线)2.5.3 直线与圆的综合-2020-2021学年高二数学课时同步练(人教A版选择性必修第一册)2023版 湘教版(2019) 选修第一册 过关斩将 第2章 2.5.2 圆的一般方程(已下线)专题2.14 直线与圆的位置关系-重难点题型检测-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)人教A版(2019) 选修第一册 数学奇书 第二章 学业评价(二十三)人教A版(2019) 选修第一册 数学奇书 第二章 直线和圆的方程 2.5.1 直线与圆的位置关系 第 2 课时 直线与圆的方程的应用上海市金山中学2019-2020学年高二上学期期末数学试题福建省厦门二中2020-2021学年高二(10月份)月考数学试题江苏省南京市田家炳高级中学2020-2021学年高二上学期10月检测数学试题(已下线)专题5.3 期末考前必做30题(解答题基础版)-2020-2021学年高二数学下学期期末专项复习(沪教版)(已下线)专题2.2 直线与圆的位置关系-《讲亮点》2021-2022学年高二数学新教材同步配套讲练(苏教版2019选择性必修第一册)(已下线)2.5 直线与圆、圆与圆的位置关系(精讲)-2021-2022学年高二数学一隅三反系列(人教A版2019选择性必修第一册)吉林省长春市十一高中2021-2022学年高二上学期第一学程考试数学试题福建省三明市四地四校2021-2022学年高二上学期期中联考协作卷数学试题广东省广州市八十九中2022-2023学年高二上学期期中数学试题河北省正定中学2021-2022学年高二上学期第二次月考数学试题浙江省湖州中学2022-2023学年高二上学期期中数学试题广东省江门市第一中学中2022-2023学年高二上学期第二次段考数学试题江苏省苏州市黄埭中学2022-2023学年高二上学期12月阶段性练习数学试题浙江省杭师附2022-2023学年高二上学期期末数学试题江西省宜春市第十中学2022-2023学年高二上学期第一次月考数学试题(已下线)专题8-1 直线与圆归类(讲+练)-2(已下线)专题2.13 直线与圆的位置关系-重难点题型精讲-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)河南省中原名校联考2023-2024学年高二上学期9月月考数学试题河南省开封市五县联考2023-2024学年高二上学期第一次月考数学试题吉林省长春市第二实验中学2023-2024学年高二上学期10月月考数学试题吉林省长春市文理高中有限责任公司2023-2024学年高二上学期10月月考数学试题(已下线)第二章 圆与方程(压轴题专练)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第一册)
名校
5 . 已知圆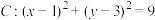 ,线段
,线段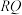 的端点
的端点 的坐标是
的坐标是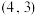 ,端点
,端点 在圆
在圆 上运动,且点
上运动,且点 满足线段
满足线段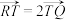 ,记
,记 点的轨迹为曲线
点的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)过点 斜率为
斜率为 的直线
的直线 与曲线
与曲线 交于
交于 ,
, 两点,试探究:
两点,试探究:
①设 为坐标原点,若
为坐标原点,若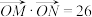 ,这样的直线
,这样的直线 是否存在,若存在求出
是否存在,若存在求出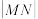 ;若不存在说明理由;
;若不存在说明理由;
②求线段 的中点
的中点 的轨迹方程.
的轨迹方程.
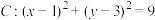 ,线段
,线段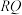 的端点
的端点 的坐标是
的坐标是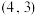 ,端点
,端点 在圆
在圆 上运动,且点
上运动,且点 满足线段
满足线段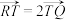 ,记
,记 点的轨迹为曲线
点的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)过点
 斜率为
斜率为 的直线
的直线 与曲线
与曲线 交于
交于 ,
, 两点,试探究:
两点,试探究:①设
 为坐标原点,若
为坐标原点,若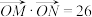 ,这样的直线
,这样的直线 是否存在,若存在求出
是否存在,若存在求出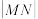 ;若不存在说明理由;
;若不存在说明理由;②求线段
 的中点
的中点 的轨迹方程.
的轨迹方程.
您最近一年使用:0次
2021-12-09更新
|
1076次组卷
|
4卷引用:直线与圆的位置关系的综合运用
解题方法
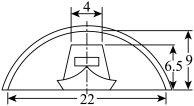
6 . 河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,可以通行无阻.近日水位暴涨了2.7m,为此,必须加重船载,降低船身,才能通过桥洞.试问:船身应该降低多少?(精确到0.1m,参考数据 )
)
 )
)
您最近一年使用:0次
2023-10-02更新
|
182次组卷
|
10卷引用:人教A版 全能练习 必修2 第四章 第二节 4.2.3 直线与圆的方程的应用
人教A版 全能练习 必修2 第四章 第二节 4.2.3 直线与圆的方程的应用(已下线)2.1 圆的方程沪教版(2020) 选修第一册 新课改一课一练 第2章 数学建模1——圆在实际中的应用2023版 湘教版(2019) 选修第一册 过关斩将 第2章 2.5.1 圆的标准方程2016-2017学年江苏沭阳县高二上期中数学试卷江苏省无锡市惠山区玉祁高中2019-2020学年高一下学期期中数学试题江苏省连云港市赣榆区赣马高级中学2022-2023学年高二上学期10月第一次检测数学试题苏教版(2019)选择性必修第一册课本习题 习题2.1(已下线)专题03 圆的方程(3大考点9种题型)(考点清单)-2023-2024学年高二数学上学期期中考点大串讲(苏教版2019选择性必修第一册)(已下线)专题17 直线与圆的位置关系9种常见考法归类- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教B版2019选择性必修第一册)
名校
解题方法
7 . 如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为 m,行车道总宽度BC为
m,行车道总宽度BC为 m,侧墙EA、FD高为2m,弧顶高MN为5m.
m,侧墙EA、FD高为2m,弧顶高MN为5m.

(1)建立直角坐标系,求圆弧所在的圆的方程;
(2)为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5m.请计算车辆通过隧道的限制高度是多少.
 m,行车道总宽度BC为
m,行车道总宽度BC为 m,侧墙EA、FD高为2m,弧顶高MN为5m.
m,侧墙EA、FD高为2m,弧顶高MN为5m.
(1)建立直角坐标系,求圆弧所在的圆的方程;
(2)为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5m.请计算车辆通过隧道的限制高度是多少.
您最近一年使用:0次
2021-11-16更新
|
380次组卷
|
12卷引用:北师大版 全能练习 必修2 第二章 2.1 圆与圆的方程
北师大版 全能练习 必修2 第二章 2.1 圆与圆的方程(已下线)4.2.3 直线与圆的方程的应用-2020-2021学年高一数学课时同步练(人教A版必修2)北京海淀育英学校2017-2018学年高二上学期期中考试数学(理)试题河南省濮阳市2019-2020学年高一上学期期末数学试题江西省南昌市第十中学2020-2021学年高二上学期第一次月考数学试题(已下线)考点44 圆的方程(考点专练)-备战2021年新高考数学一轮复习考点微专题安徽省宣城市广德市实验中学2020-2021学年高二上学期10月月考数学试题福建省华安县第一中学2020-2021学年高二上学期期中考试数学试题(已下线)专题2.15 圆与圆的位置关系-重难点题型精讲-2021-2022学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)专题2.15 圆与圆的位置关系-重难点题型精讲-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)第2章 圆与方程 综合测试-【暑假自学课】2023年新高二数学暑假精品课(苏教版2019必修第一册)广东省广州市广州四中2023-2024学年高二上学期12月月考数学试题
8 . 如图,圆 ,点
,点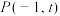 为直线
为直线 上一动点,过点
上一动点,过点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.
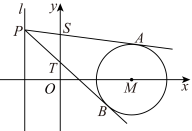
(1)若 ,求切线所在直线方程;
,求切线所在直线方程;
(2)求 的最小值;
的最小值;
(3)若两条切线 与
与 轴分别交于
轴分别交于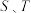 两点,求
两点,求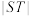 的最小值.
的最小值.
 ,点
,点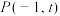 为直线
为直线 上一动点,过点
上一动点,过点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.
(1)若
 ,求切线所在直线方程;
,求切线所在直线方程;(2)求
 的最小值;
的最小值;(3)若两条切线
 与
与 轴分别交于
轴分别交于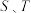 两点,求
两点,求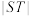 的最小值.
的最小值.
您最近一年使用:0次
2019-05-07更新
|
3857次组卷
|
16卷引用:2.6+章末复习课(重点练)-2020-2021学年高二数学十分钟同步课堂专练(人教A版选择性必修第一册)
(已下线)2.6+章末复习课(重点练)-2020-2021学年高二数学十分钟同步课堂专练(人教A版选择性必修第一册)苏教版(2019) 选修第一册 选填专练 第2章 大题规范练【校级联考】江苏省无锡市江阴四校2018-2019学年高一下学期期中考试数学试题(已下线)【新东方】杭州高二数学试卷233(已下线)【新东方】杭州高二数学试卷242浙江省杭州市高级中学2019-2020学年高二上学期期中数学试题重庆市缙云教育联盟2020-2021学年高二上学期10月月考数学试题(已下线)【新东方】杭州新东方高中数学试卷338安徽省安庆市第一中学2020-2021学年高二上学期期中数学试题河北省实验中学2022届高三上学期开学考试数学试题广东省广州市部分学校2021-2022学年高二上学期期中联考数学试题新疆乌鲁木齐市第八中学2021-2022学年高二上学期第一次月考数学试题(已下线)专题13 《圆与方程》中的动点动直线问题(1)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)(已下线)专题04 《圆与方程》中的易错题(2)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)江苏省镇江市句容碧桂园学校2022-2023学年高二上学期期中模拟数学试题山东省济南市历城区历城第二中学2022-2023学年高二上学期期中数学试题
名校
9 . 已知直线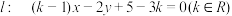 恒过定点
恒过定点 ,圆
,圆 经过点
经过点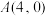 和点
和点 ,且圆心在直线
,且圆心在直线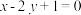 上.
上.
(1)求定点 的坐标与圆
的坐标与圆 的方程;
的方程;
(2)已知点 为圆
为圆 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点 ,问:在
,问:在 轴上是否存在一点
轴上是否存在一点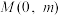 ,使得
,使得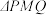 为直角三角形,若存在,求出
为直角三角形,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
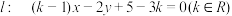 恒过定点
恒过定点 ,圆
,圆 经过点
经过点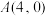 和点
和点 ,且圆心在直线
,且圆心在直线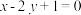 上.
上.(1)求定点
 的坐标与圆
的坐标与圆 的方程;
的方程;(2)已知点
 为圆
为圆 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点 ,问:在
,问:在 轴上是否存在一点
轴上是否存在一点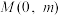 ,使得
,使得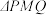 为直角三角形,若存在,求出
为直角三角形,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
您最近一年使用:0次
2019-12-06更新
|
684次组卷
|
6卷引用:4.2.3 直线与圆的方程的应用-2020-2021学年高一数学课时同步练(人教A版必修2)
(已下线)4.2.3 直线与圆的方程的应用-2020-2021学年高一数学课时同步练(人教A版必修2)山东省烟台市2016-2017学年高一下学期期中考试数学试题江西省南昌二中2017-2018学年度上学期第一次月考高二数学试题江西省南昌市第二中学2017-2018学年高二上学期第一次月考数学(理)试题江西省南昌市第二中学2019-2020学年高二上学期期中数学(理)试题江西省南昌市第二中学2020—2021学年高二文科上学期期中考试数学试题
名校
10 . 已知圆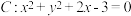 ,直线
,直线 与圆
与圆 相交于不同的两点
相交于不同的两点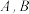 ,点
,点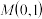 是线段
是线段 的中点.
的中点.
(1)求直线 的方程;
的方程;
(2)是否存在与直线 平行的直线
平行的直线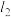 ,使得
,使得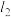 与与圆
与与圆 相交于不同的两点
相交于不同的两点 ,
,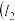 不经过点
不经过点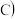 ,且
,且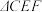 的面积
的面积 最大?若存在,求出
最大?若存在,求出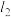 的方程及对应的
的方程及对应的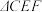 的面积S;若不存在,请说明理由.
的面积S;若不存在,请说明理由.
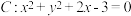 ,直线
,直线 与圆
与圆 相交于不同的两点
相交于不同的两点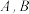 ,点
,点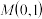 是线段
是线段 的中点.
的中点.(1)求直线
 的方程;
的方程;(2)是否存在与直线
 平行的直线
平行的直线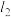 ,使得
,使得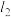 与与圆
与与圆 相交于不同的两点
相交于不同的两点 ,
,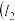 不经过点
不经过点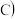 ,且
,且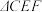 的面积
的面积 最大?若存在,求出
最大?若存在,求出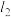 的方程及对应的
的方程及对应的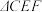 的面积S;若不存在,请说明理由.
的面积S;若不存在,请说明理由.
您最近一年使用:0次
2019-04-17更新
|
621次组卷
|
5卷引用:人教B版(2019) 选修第一册 过关检测 第二章 第2.3节 综合把关练



