1 . 甲、乙两位同学组成学习小组进行项目式互助学习,在共同完成某个内容的互助学习后,甲、乙都参加了若干次测试,现从甲的测试成绩里随机抽取了7次成绩,从乙的测试成绩里随机抽取了9次成绩,数据如下:
甲:93 95 81 72 80 82 92
乙:85 82 77 80 94 86 92 84 85
经计算得出甲、乙两人的测试成绩的平均数均为85.
(1)求甲乙两位同学测试成绩的方差;
(2)为检验两组数据的差异性是否显著,可以计算统计量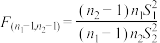 ,其中
,其中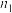 个数据的方差为
个数据的方差为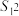 ,
,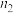 个数据的方差为
个数据的方差为 ,且
,且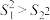 .若
.若 ,则认为两组数据有显著性差异,否则不能认为两组数据有显著性差异.若
,则认为两组数据有显著性差异,否则不能认为两组数据有显著性差异.若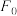 的临界值采用下表中的数据:
的临界值采用下表中的数据:
例如: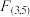 对应的临界值
对应的临界值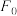 为5.41.请根据以上资料判断甲、乙两位同学进行项目式互助学习的效果是否有显著性差异.
为5.41.请根据以上资料判断甲、乙两位同学进行项目式互助学习的效果是否有显著性差异.
甲:93 95 81 72 80 82 92
乙:85 82 77 80 94 86 92 84 85
经计算得出甲、乙两人的测试成绩的平均数均为85.
(1)求甲乙两位同学测试成绩的方差;
(2)为检验两组数据的差异性是否显著,可以计算统计量
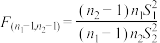 ,其中
,其中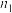 个数据的方差为
个数据的方差为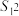 ,
,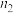 个数据的方差为
个数据的方差为 ,且
,且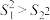 .若
.若 ,则认为两组数据有显著性差异,否则不能认为两组数据有显著性差异.若
,则认为两组数据有显著性差异,否则不能认为两组数据有显著性差异.若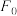 的临界值采用下表中的数据:
的临界值采用下表中的数据:
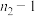 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 |
2 | 18.5 | 19.0 | 19.2 | 19.2 | 19.3 | 19.3 | 19.4 | 19.4 |
3 | 10.1 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8.85 |
4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 |
5 | 6.61 | 5.79 | 5.41 | 6.19 | 5.05 | 4.95 | 4.88 | 4.82 |
6 | 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 |
7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 |
8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 |
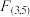 对应的临界值
对应的临界值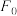 为5.41.请根据以上资料判断甲、乙两位同学进行项目式互助学习的效果是否有显著性差异.
为5.41.请根据以上资料判断甲、乙两位同学进行项目式互助学习的效果是否有显著性差异.
您最近一年使用:0次
2024高一下·全国·专题练习
2 . 甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表:
下列结论中,正确的是( )
| 班级 | 参加人数 | 中位数 | 方差 | 平均数 |
| 甲 | 55 | 149 | 191 | 135 |
| 乙 | 55 | 151 | 110 | 135 |
| A.甲、乙两班学生成绩的平均水平相同 |
B.乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数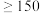 个为优秀) 个为优秀) |
| C.甲班的成绩波动情况比乙班的成绩波动大 |
| D.甲班成绩的众数小于乙班成绩的众数 |
您最近一年使用:0次
解题方法
3 . 为提升学生用数学知识解决现实生活或其他学科领域中的问题的能力,发展学生数学建模素养,某市面向全市高中学生开展数学建模论文征文活动.对于参加征文活动的每篇论文,由两位评委独立评分,取两位评委评分的平均数作为该篇论文的初评得分.从评委甲和评委乙负责评审的论文中随机抽取10篇,这10篇论文的评分情况如下表所示.
(1)从这 篇论文中随机抽取1篇,求甲、乙两位评委的评分之差的绝对值不超过
篇论文中随机抽取1篇,求甲、乙两位评委的评分之差的绝对值不超过 的概率;
的概率;
(2)从这 篇论文中随机抽取3篇,甲、乙两位评委对同一篇论文的评分之差的绝对值不超过
篇论文中随机抽取3篇,甲、乙两位评委对同一篇论文的评分之差的绝对值不超过 的篇数记为
的篇数记为 ,求
,求 的分布列及数学期望;
的分布列及数学期望;
(3)对于序号为 的论文,设评委甲的评分为
的论文,设评委甲的评分为 ,评委乙的评分为
,评委乙的评分为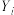 ,分别记甲、乙两位评委对这10篇论文评分的平均数为
,分别记甲、乙两位评委对这10篇论文评分的平均数为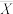 ,
, ,标准差为
,标准差为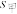 ,
,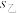 ,以
,以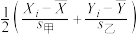 作为序号为
作为序号为 的论文的标准化得分.对这10篇论文按照初评得分与标准化得分分别从高到低进行排名,判断序号为2的论文的两种排名结果是否相同?(结论不要求证明)
的论文的标准化得分.对这10篇论文按照初评得分与标准化得分分别从高到低进行排名,判断序号为2的论文的两种排名结果是否相同?(结论不要求证明)
| 序号 | 评委甲评分 | 评委乙评分 | 初评得分 |
| 1 | 67 | 82 | 74.5 |
| 2 | 80 | 86 | 83 |
| 3 | 61 | 76 | 68.5 |
| 4 | 78 | 84 | 81 |
| 5 | 70 | 85 | 77.5 |
| 6 | 81 | 83 | 82 |
| 7 | 84 | 86 | 85 |
| 8 | 68 | 74 | 71 |
| 9 | 66 | 77 | 71.5 |
| 10 | 64 | 82 | 73 |
 篇论文中随机抽取1篇,求甲、乙两位评委的评分之差的绝对值不超过
篇论文中随机抽取1篇,求甲、乙两位评委的评分之差的绝对值不超过 的概率;
的概率;(2)从这
 篇论文中随机抽取3篇,甲、乙两位评委对同一篇论文的评分之差的绝对值不超过
篇论文中随机抽取3篇,甲、乙两位评委对同一篇论文的评分之差的绝对值不超过 的篇数记为
的篇数记为 ,求
,求 的分布列及数学期望;
的分布列及数学期望;(3)对于序号为
 的论文,设评委甲的评分为
的论文,设评委甲的评分为 ,评委乙的评分为
,评委乙的评分为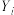 ,分别记甲、乙两位评委对这10篇论文评分的平均数为
,分别记甲、乙两位评委对这10篇论文评分的平均数为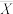 ,
, ,标准差为
,标准差为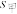 ,
,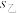 ,以
,以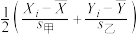 作为序号为
作为序号为 的论文的标准化得分.对这10篇论文按照初评得分与标准化得分分别从高到低进行排名,判断序号为2的论文的两种排名结果是否相同?(结论不要求证明)
的论文的标准化得分.对这10篇论文按照初评得分与标准化得分分别从高到低进行排名,判断序号为2的论文的两种排名结果是否相同?(结论不要求证明)
您最近一年使用:0次
名校
4 . 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示
(2)请从四个不同的角度对这次测试进行分析:
①从平均数与方差相结合的角度分析偏离程度;
②从平均数与中位数相结合的角度分析谁的成绩好些;
③从平均数和命中9环以上的次数看谁的成绩好些;
④从折线图上两人射击命中环数及走势分析谁更好.

| 平均数 | 方差 | 中位数 | 命中9环及以上 | |
| 甲 | 1.2 | 7 | ||
| 乙 | 3 |
(2)请从四个不同的角度对这次测试进行分析:
①从平均数与方差相结合的角度分析偏离程度;
②从平均数与中位数相结合的角度分析谁的成绩好些;
③从平均数和命中9环以上的次数看谁的成绩好些;
④从折线图上两人射击命中环数及走势分析谁更好.
您最近一年使用:0次
解题方法
5 . 滨海盐碱地是我国盐碱地的主要类型之一,如何利用更有效的方法改造这些宝贵的土地资源,成为摆在我们面前的世界级难题.对盐碱的治理方法,研究人员在长期的实践中获得了两种成本差异不大,且能降低滨海盐碱地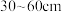 土壤层可溶性盐含量的技术,为了对比两种技术治理盐碱的效果,科研人员在同一区域采集了12个土壤样本,平均分成A、B两组,测得A组土壤可溶性盐含量数据样本平均数
土壤层可溶性盐含量的技术,为了对比两种技术治理盐碱的效果,科研人员在同一区域采集了12个土壤样本,平均分成A、B两组,测得A组土壤可溶性盐含量数据样本平均数 ,方差
,方差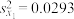 ,B组土壤可溶性盐含量数据样本平均数
,B组土壤可溶性盐含量数据样本平均数 ,方差
,方差 .用技术1对A组土壤进行可溶性盐改良试验,用技术2对B组土壤进行可溶性盐改良试验,分别获得改良后土壤可溶性盐含量数据如下:
.用技术1对A组土壤进行可溶性盐改良试验,用技术2对B组土壤进行可溶性盐改良试验,分别获得改良后土壤可溶性盐含量数据如下:
改良后A组、B组土壤可溶性盐含量数据样本平均数分别为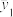 和
和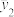 ,样本方差分别记为
,样本方差分别记为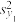 和
和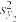 .
.
(1)求 ;
;
(2)应用技术1与技术2土壤可溶性盐改良试验后,土壤可溶性盐含量是否有显著降低?(若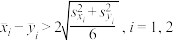 ,则认为技术能显著降低土壤可溶性盐含量,否则不认为有显著降低.)
,则认为技术能显著降低土壤可溶性盐含量,否则不认为有显著降低.)
 土壤层可溶性盐含量的技术,为了对比两种技术治理盐碱的效果,科研人员在同一区域采集了12个土壤样本,平均分成A、B两组,测得A组土壤可溶性盐含量数据样本平均数
土壤层可溶性盐含量的技术,为了对比两种技术治理盐碱的效果,科研人员在同一区域采集了12个土壤样本,平均分成A、B两组,测得A组土壤可溶性盐含量数据样本平均数 ,方差
,方差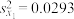 ,B组土壤可溶性盐含量数据样本平均数
,B组土壤可溶性盐含量数据样本平均数 ,方差
,方差 .用技术1对A组土壤进行可溶性盐改良试验,用技术2对B组土壤进行可溶性盐改良试验,分别获得改良后土壤可溶性盐含量数据如下:
.用技术1对A组土壤进行可溶性盐改良试验,用技术2对B组土壤进行可溶性盐改良试验,分别获得改良后土壤可溶性盐含量数据如下:A组 | 0.66 | 0.68 | 0.69 | 0.71 | 0.72 | 0.74 |
B组 | 0.46 | 0.48 | 0.49 | 0.49 | 0.51 | 0.54 |
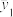 和
和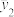 ,样本方差分别记为
,样本方差分别记为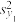 和
和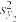 .
.(1)求
 ;
;(2)应用技术1与技术2土壤可溶性盐改良试验后,土壤可溶性盐含量是否有显著降低?(若
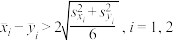 ,则认为技术能显著降低土壤可溶性盐含量,否则不认为有显著降低.)
,则认为技术能显著降低土壤可溶性盐含量,否则不认为有显著降低.)
您最近一年使用:0次
解题方法
6 . 在去年某校高二年级“校长杯”足球比赛中,甲乙两班每场比赛平均进球数、失球数及所有场次比赛进球个数、失球个数的标准差如下表:
下列说法正确的是( )
| 进球个数平均数 | 失球个数平均数 | 进球个数标准差 | 失球个数标准差 | |
| 甲班 | 2.3 | 1.5 | 0.5 | 1.1 |
| 乙班 | 1.4 | 2.1 | 1.2 | 0.4 |
| A.甲班在防守中比乙班稳定 |
| B.乙班总体实力优于甲班 |
| C.乙班很少不失球 |
| D.乙班在进攻中有时表现很好有时表现较差 |
您最近一年使用:0次
2024·全国·模拟预测
7 . 某杨梅种植户从购买客户中随机抽取20位客户做质量随访调查,其中购买 系列(大棚种植)的10位,购买
系列(大棚种植)的10位,购买 系列(自然种植)的10位,从杨梅的大小、口感、水分、甜度进行综合打分(满分100分),打分结果记录如下:
系列(自然种植)的10位,从杨梅的大小、口感、水分、甜度进行综合打分(满分100分),打分结果记录如下:
 系列(大棚种植):84 81 79 76 95 88 93 86 86 92
系列(大棚种植):84 81 79 76 95 88 93 86 86 92
 系列(自然种植):92 95 80 75 83 87 90 80 85 93
系列(自然种植):92 95 80 75 83 87 90 80 85 93
(1)分别写出这两个系列综合打分的中位数.
(2)分别求出这两个系列综合打分的平均数与方差,通过上述数据结果进行分析,你认为推广哪种系列种植更合适?
 系列(大棚种植)的10位,购买
系列(大棚种植)的10位,购买 系列(自然种植)的10位,从杨梅的大小、口感、水分、甜度进行综合打分(满分100分),打分结果记录如下:
系列(自然种植)的10位,从杨梅的大小、口感、水分、甜度进行综合打分(满分100分),打分结果记录如下: 系列(大棚种植):84 81 79 76 95 88 93 86 86 92
系列(大棚种植):84 81 79 76 95 88 93 86 86 92 系列(自然种植):92 95 80 75 83 87 90 80 85 93
系列(自然种植):92 95 80 75 83 87 90 80 85 93(1)分别写出这两个系列综合打分的中位数.
(2)分别求出这两个系列综合打分的平均数与方差,通过上述数据结果进行分析,你认为推广哪种系列种植更合适?
您最近一年使用:0次
8 . 某高中为配合爱国主义教育,开展国防科技知识竞赛,预赛后,将成绩最好的甲、乙两个班学生(每班都是40人)的得分情况做成如下的条形图(20道单项选择题,每题5分,满分100分).记甲、乙两班学生得分的平均数分别为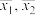 ,方差分别为
,方差分别为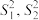 ,已求得
,已求得


(1)分别求出甲、乙两班的学生得分为95分及以上的频率;
(2)试计算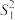 ,并判断哪个班的学生的成绩波动更小.
,并判断哪个班的学生的成绩波动更小.
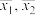 ,方差分别为
,方差分别为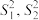 ,已求得
,已求得


(1)分别求出甲、乙两班的学生得分为95分及以上的频率;
(2)试计算
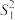 ,并判断哪个班的学生的成绩波动更小.
,并判断哪个班的学生的成绩波动更小.
您最近一年使用:0次
9 . 采购经理指数(PMI)是国际上通用的监测宏观经济走势的指标,具有较强的预测、预警作用.2023年12月31日,国家统计局发布了中国制造业PMI指数(经季节调整)图,如下图所示,则下列说法正确的是( )
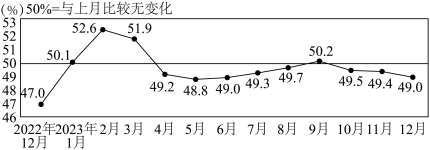
A.图中前三个数据的平均值为 |
| B.2023年四个季度的PMI指数中,第一季度方差最大 |
C.图中PMI指数的极差为 |
D.2023年PMI指数的 分位数为 分位数为 |
您最近一年使用:0次
10 . 某单位共有A、B两部门,1月份进行服务满意度问卷调查,得到两部门服务满意度得分的频率分布条形图如下.设A、B两部门的服务满意度得分的第75百分位数分别为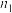 ,
,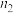 ,方差分别为
,方差分别为 ,
, ,则( )
,则( )
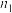 ,
,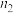 ,方差分别为
,方差分别为 ,
, ,则( )
,则( )
A. , , | B. , , |
C.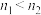 , , | D.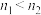 , , |
您最近一年使用:0次
2024-03-20更新
|
1429次组卷
|
6卷引用:9.2.3总体离散程度的估计
(已下线)9.2.3总体离散程度的估计(已下线)第14章 统计单元综合能力测试卷-【帮课堂】(苏教版2019必修第二册)(已下线)9.2.4总体离散程度的估计(分层练习)-【上好课】(人教A版2019必修第二册)2024届福建省高三下学期数学适应性练习卷上海市崇明区2024届高三二模数学试题(已下线)第14章 统计(提升卷)-重难点突破及混淆易错规避(苏教版2019必修第二册)






