1 . 杨辉是我国古代数学史上一位著述丰富的数学家,著有《详解九章算法》、《日用算法》和《杨辉算法》,杨辉在1261年所著的《详解九章算法》给出了如下图1所示的表,我们称这个表为杨辉三角,图2是杨辉三角的数字表示,杨辉三角的发现要比欧洲早500年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.
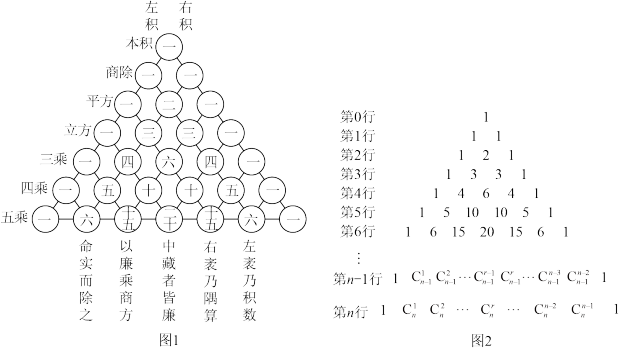
杨辉三角本身包含了很多有趣的性质,利用这些性质,可以解决很多数学问题.
性质1:杨辉三角的第 行就是
行就是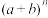 的展开式的二项式系数;
的展开式的二项式系数;
性质2(对称性):每行中与首末两端“等距离”之数相等,即 ;
;
性质3(递归性):除1以外的数都等于肩上两数之和,即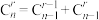 ;
;
性质4:自腰上的某个1开始平行于腰的一条线上的连续 个数的和等于最后一个数斜右下方的那个数,比如:
个数的和等于最后一个数斜右下方的那个数,比如: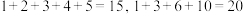 ;
;
请回答以下问题:
(1)求杨辉三角中第8行的各数之和;
(2)证明: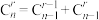 ;
;
(3)在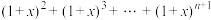 的展开式中,求含
的展开式中,求含 项的系数.
项的系数.

杨辉三角本身包含了很多有趣的性质,利用这些性质,可以解决很多数学问题.
性质1:杨辉三角的第
 行就是
行就是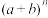 的展开式的二项式系数;
的展开式的二项式系数;性质2(对称性):每行中与首末两端“等距离”之数相等,即
 ;
;性质3(递归性):除1以外的数都等于肩上两数之和,即
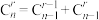 ;
;性质4:自腰上的某个1开始平行于腰的一条线上的连续
 个数的和等于最后一个数斜右下方的那个数,比如:
个数的和等于最后一个数斜右下方的那个数,比如: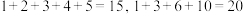 ;
;请回答以下问题:
(1)求杨辉三角中第8行的各数之和;
(2)证明:
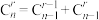 ;
;(3)在
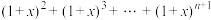 的展开式中,求含
的展开式中,求含 项的系数.
项的系数.
您最近半年使用:0次
2023-07-25更新
|
622次组卷
|
9卷引用:安徽省芜湖市2022-2023学年高二下学期教学质量统测数学试题
安徽省芜湖市2022-2023学年高二下学期教学质量统测数学试题(已下线)第07讲 二项式定理-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)第06讲 第六章 计数原理 章末题型大总结(4)(已下线)专题6.3 二项式定理【九大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)2023-2024学年高二下学期第一次月考解答题压轴题十六大题型专练(3)(已下线)6.3二项式定理 第三练 能力提升拔高(已下线)模块四 专题1 高考新题型专练(新定义专练)(人教A)(高二)(已下线)2023-2024学年高二下学期期中复习解答题压轴题十七大题型专练(2)(已下线)模块五 专题1 全真基础模拟1
2 . (1)已知 是自然数,
是自然数, 是正整数,且
是正整数,且 .证明组合数性质:
.证明组合数性质: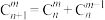 ;
;
(2)按(1)中的组合数性质公式,有 .请自编一个计数问题,使得
.请自编一个计数问题,使得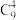 与
与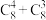 为该问题的两个不同的解法,并简要说明解法的依据.
为该问题的两个不同的解法,并简要说明解法的依据.
 是自然数,
是自然数, 是正整数,且
是正整数,且 .证明组合数性质:
.证明组合数性质: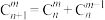 ;
;(2)按(1)中的组合数性质公式,有
 .请自编一个计数问题,使得
.请自编一个计数问题,使得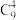 与
与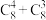 为该问题的两个不同的解法,并简要说明解法的依据.
为该问题的两个不同的解法,并简要说明解法的依据.
您最近半年使用:0次
名校
解题方法
3 . 五一小长假到来,多地迎来旅游高峰期,各大旅游景点都推出了种种新奇活动以吸引游客,小明去成都某熊猫基地游玩时,发现了一个趣味游戏,游戏规则为:在一个足够长的直线轨道的中心处有一个会走路的机器人,游客可以设定机器人总共行走的步数,机器人每一步会随机选择向前行走或向后行走,且每一步的距离均相等,若机器人走完这些步数后,恰好回到初始位置,则视为胜利.
(1)若小明设定机器人一共行走4步,记机器人的最终位置与初始位置的距离为 步,求
步,求 的分布列和期望;
的分布列和期望;
(2)记 为设定机器人一共行走
为设定机器人一共行走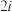 步时游戏胜利的概率,求
步时游戏胜利的概率,求 ,并判断当
,并判断当 为何值时,游戏胜利的概率最大;
为何值时,游戏胜利的概率最大;
(3)该基地临时修改了游戏规则,要求机器人走完设定的步数后,恰好第一次回到初始位置,才视为胜利.小明发现,利用现有的知识无法推断设定多少步时获得胜利的概率最大,于是求助正在读大学的哥哥,哥哥告诉他,“卡特兰数”可以帮助他解决上面的疑惑:将 个0和
个0和 个1排成一排,若对任意的
个1排成一排,若对任意的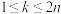 ,在前
,在前 个数中,0的个数都不少于1的个数,则满足条件的排列方式共有
个数中,0的个数都不少于1的个数,则满足条件的排列方式共有 种,其中,
种,其中, 的结果被称为卡特兰数.若记
的结果被称为卡特兰数.若记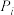 为设定机器人行走
为设定机器人行走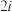 步时恰好第一次回到初始位置的概率,证明:对(2)中的
步时恰好第一次回到初始位置的概率,证明:对(2)中的 ,有
,有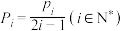
(1)若小明设定机器人一共行走4步,记机器人的最终位置与初始位置的距离为
 步,求
步,求 的分布列和期望;
的分布列和期望;(2)记
 为设定机器人一共行走
为设定机器人一共行走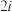 步时游戏胜利的概率,求
步时游戏胜利的概率,求 ,并判断当
,并判断当 为何值时,游戏胜利的概率最大;
为何值时,游戏胜利的概率最大;(3)该基地临时修改了游戏规则,要求机器人走完设定的步数后,恰好第一次回到初始位置,才视为胜利.小明发现,利用现有的知识无法推断设定多少步时获得胜利的概率最大,于是求助正在读大学的哥哥,哥哥告诉他,“卡特兰数”可以帮助他解决上面的疑惑:将
 个0和
个0和 个1排成一排,若对任意的
个1排成一排,若对任意的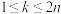 ,在前
,在前 个数中,0的个数都不少于1的个数,则满足条件的排列方式共有
个数中,0的个数都不少于1的个数,则满足条件的排列方式共有 种,其中,
种,其中, 的结果被称为卡特兰数.若记
的结果被称为卡特兰数.若记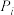 为设定机器人行走
为设定机器人行走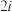 步时恰好第一次回到初始位置的概率,证明:对(2)中的
步时恰好第一次回到初始位置的概率,证明:对(2)中的 ,有
,有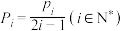
您最近半年使用:0次
2023-05-02更新
|
2575次组卷
|
7卷引用:湖南省长沙市第一中学2022-2023学年高二下学期期末数学试题
湖南省长沙市第一中学2022-2023学年高二下学期期末数学试题湖北省圆梦杯2023届高三下学期统一模拟(二)数学试题(已下线)第四篇 概率与统计 专题2 最可能成功次数 微点2 最可能成功次数综合训练重庆市2023届高三下学期5月月度质量检测数学试题(已下线)微考点8-1 新高考新题型19题新定义题型精选(已下线)专题04 概率统计大题(已下线)专题21 概率与统计的综合运用(13大核心考点)(讲义)
4 . (1)求证: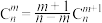 ;
;
(2)求证: ;
;
(3)若m、n、r均为正整数,试证明: .
.
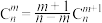 ;
;(2)求证:
 ;
;(3)若m、n、r均为正整数,试证明:
 .
.
您最近半年使用:0次
5 . 杨辉三角形,又称贾宪三角形,是二项式系数 (
(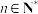 ,
,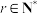 且
且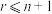 )在三角形中的一种几何排列,北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算,南宋时期杭州人杨辉在他1261年所著的《详解九章算法》一书中,辑录了如下图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪前半贾宪的《释锁算术》,并绘画了“古法七乘方图”,故此,杨辉三角又被称为“贾宪三角”,杨辉三角形的构造法则为:三角形的两个腰都是由数字1组成的,其余的数都等于它肩上的两个数字相加.根据以上信息及二项式定理的相关知识分析,下列说法中正确的是( )
)在三角形中的一种几何排列,北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算,南宋时期杭州人杨辉在他1261年所著的《详解九章算法》一书中,辑录了如下图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪前半贾宪的《释锁算术》,并绘画了“古法七乘方图”,故此,杨辉三角又被称为“贾宪三角”,杨辉三角形的构造法则为:三角形的两个腰都是由数字1组成的,其余的数都等于它肩上的两个数字相加.根据以上信息及二项式定理的相关知识分析,下列说法中正确的是( )

 (
(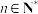 ,
,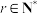 且
且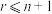 )在三角形中的一种几何排列,北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算,南宋时期杭州人杨辉在他1261年所著的《详解九章算法》一书中,辑录了如下图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪前半贾宪的《释锁算术》,并绘画了“古法七乘方图”,故此,杨辉三角又被称为“贾宪三角”,杨辉三角形的构造法则为:三角形的两个腰都是由数字1组成的,其余的数都等于它肩上的两个数字相加.根据以上信息及二项式定理的相关知识分析,下列说法中正确的是( )
)在三角形中的一种几何排列,北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算,南宋时期杭州人杨辉在他1261年所著的《详解九章算法》一书中,辑录了如下图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪前半贾宪的《释锁算术》,并绘画了“古法七乘方图”,故此,杨辉三角又被称为“贾宪三角”,杨辉三角形的构造法则为:三角形的两个腰都是由数字1组成的,其余的数都等于它肩上的两个数字相加.根据以上信息及二项式定理的相关知识分析,下列说法中正确的是( )
A.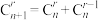 |
B.当 且 且 时, 时,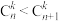 |
C.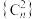 为等差数列 为等差数列 |
D.存在 ,使得 ,使得 为等差数列 为等差数列 |
您最近半年使用:0次
6 . (1)解不等式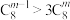 ;
;
(2)求证:① ,
,
②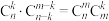 .
.
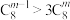 ;
;(2)求证:①
 ,
,②
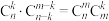 .
.
您最近半年使用:0次
2022-02-21更新
|
914次组卷
|
7卷引用:第三章 排列、组合与二项式定理(A卷·知识通关练)(1)
(已下线)第三章 排列、组合与二项式定理(A卷·知识通关练)(1)(已下线)6.2.3组合+6.2.4组合数 (精讲)(1)新疆维吾尔自治区乌鲁木齐市2022-2023学年高二下学期7月期末考试数学试题河北省高碑店市崇德实验中学2020-2021学年高二下学期4月月考数学试题(已下线)第6章 计数原理(单元提升卷)-2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)(已下线)6.2.3组合-6.2.4组合数——课时作业(基础版)(已下线)12.1 排列与组合-1
7 . 求证: .
.
 .
.
您最近半年使用:0次
20-21高二·全国·课后作业
解题方法
8 . 杨辉三角是杨辉的一项重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律,如图是一个11阶杨辉三角:
(2)求n阶(包括0阶)杨辉三角的所有数的和;
(3)在第2斜列中,前5个数依次为1,3,6,10,15;第3斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m-1斜列中(从右上到左下)前k个数之和,一定等于第m斜列中第k个数.试用含有m,k(m,k∈N*)的数字公式表示上述结论,并给予证明.

(2)求n阶(包括0阶)杨辉三角的所有数的和;
(3)在第2斜列中,前5个数依次为1,3,6,10,15;第3斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m-1斜列中(从右上到左下)前k个数之和,一定等于第m斜列中第k个数.试用含有m,k(m,k∈N*)的数字公式表示上述结论,并给予证明.
您最近半年使用:0次



