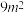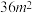| A.45.606 | B.45.6 | C.45.56 | D.45.51 |
【知识点】 利用二次函数模型解决实际问题
 与价格
与价格 之间的关系最可能是下图中的( )
之间的关系最可能是下图中的( )A. | B.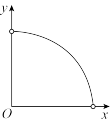 | C.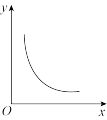 | D.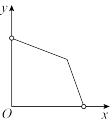 |
【知识点】 分式型函数模型的应用
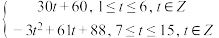 ,为了保证赛会期间运动员都能按时参赛,主办方应至少准备大巴车的数量是( )
,为了保证赛会期间运动员都能按时参赛,主办方应至少准备大巴车的数量是( )| A.7 | B.8 | C.9 | D.10 |
【知识点】 分段函数模型的应用
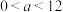 ,不考虑树的粗细,现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD,设此矩形花圃的最大面积为S(单位:
,不考虑树的粗细,现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD,设此矩形花圃的最大面积为S(单位: ),若将这棵树围在花圃内,则函数
),若将这棵树围在花圃内,则函数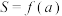 的图象大致是( )
的图象大致是( )
A.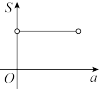 | B.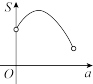 | C.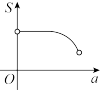 | D.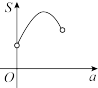 |
【知识点】 根据实际问题作函数图象 分段函数模型的应用
A. | B.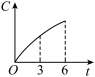 |
C.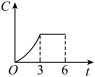 | D.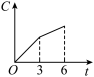 |
【知识点】 分段函数模型的应用
A.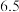 元 元 | B. 元 元 | C.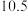 元 元 | D.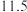 元 元 |
【知识点】 分段函数模型的应用
| A.10吨 | B.13吨 | C.11吨 | D.9吨 |
【知识点】 分段函数模型的应用
| A.2元 | B.2.5元 |
| C.1元 | D.1.5元 |
【知识点】 利用二次函数模型解决实际问题
设某公司原有员工100人从事产品A的生产,平均每人每年创造产值t万元(t为正常数).公司决定从原有员工中分流x(0<x<100,x∈N+)人去进行新开发的产品B的生产.分流后,继续从事产品A生产的员工平均每人每年创造产值在原有的基础上增长了1.2x%.若要保证产品A的年产值不减少,则最多能分流的人数是( )
| A.15 | B.16 |
| C.17 | D.18 |
【知识点】 分段函数模型的应用
 ,若每件产品的售价为25万元,则该厂获得最大利润时,生产的产品件数为( )
,若每件产品的售价为25万元,则该厂获得最大利润时,生产的产品件数为( )| A.52 | B.53或54 | C.53 | D.52或53 |
【知识点】 利用二次函数模型解决实际问题
 的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
| A.上午10:00 | B.中午12:00 | C.下午4:00 | D.下午6:00 |
【知识点】 分段函数模型的应用

①骑自行车者比骑摩托车者早出发3 h,晚到1 h;
②骑自行车者是变速运动,骑摩托车者是匀速运动;
③骑摩托车者在出发1.5 h后追上了骑自行车者;
④骑摩托车者在出发1.5 h后与骑自行车者速度一样.
其中,正确信息的序号是
【知识点】 分段函数模型的应用
【知识点】 分段函数模型的应用
【知识点】 利用二次函数模型解决实际问题
 与时刻x(时)的函数关系为
与时刻x(时)的函数关系为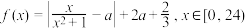 ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且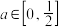 .按规定,若每天污染指数不超过2,则环保合格,否则需要整改.如果以每天中
.按规定,若每天污染指数不超过2,则环保合格,否则需要整改.如果以每天中 的最大值作为当天的污染指数,并记为
的最大值作为当天的污染指数,并记为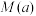 ,那么该地区污染指数的超标情况为
,那么该地区污染指数的超标情况为【知识点】 分段函数模型的应用
 元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.若使租赁公司的月收益最大,每辆车的月租金应该定为
元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.若使租赁公司的月收益最大,每辆车的月租金应该定为【知识点】 利用二次函数模型解决实际问题
 元,售价为
元,售价为 元时每天能卖出
元时每天能卖出 件.若售价每提高
件.若售价每提高 元,每天销量就减少
元,每天销量就减少 件,问商家定价为
件,问商家定价为【知识点】 利用二次函数模型解决实际问题
 如图所示
如图所示 ,则围成场地的最大面积为
,则围成场地的最大面积为 围墙厚度不计
围墙厚度不计 .
.
【知识点】 利用二次函数模型解决实际问题
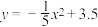 的一部分,如图所示,若命中篮圈中心,则他与篮底的距离
的一部分,如图所示,若命中篮圈中心,则他与篮底的距离 是
是
【知识点】 利用二次函数模型解决实际问题
 米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树
米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树 米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为
米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为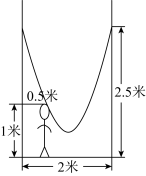
【知识点】 利用二次函数模型解决实际问题
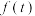 与时间
与时间 满足关系
满足关系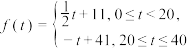
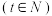 ,销售量
,销售量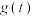 与时间
与时间 满足关系
满足关系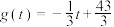
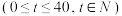 则这种商品的日销售额(销售量与价格之积)的最大值为
则这种商品的日销售额(销售量与价格之积)的最大值为【知识点】 分段函数模型的应用
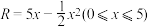 ,其中x是产品生产并售出的数量(单位:百台).
,其中x是产品生产并售出的数量(单位:百台).(1)把利润表示为年产量的函数.
(2)年产量为多少时,企业所得利润最大?
(3)年产量为多少时,企业才不亏本(不赔钱)?
【知识点】 利用二次函数模型解决实际问题 分段函数模型的应用
【知识点】 利用二次函数模型解决实际问题
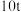 的部分为2.20元/
的部分为2.20元/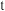 ;超过
;超过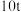 不超过
不超过 的部分为2.80元/
的部分为2.80元/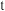 ;超过
;超过 部分为3.20元/
部分为3.20元/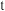 .
.(1)试求居民月水费y(元)关于用水量
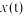 的函数关系式;
的函数关系式;(2)某户居民4月份用水
 ,应交水费多少元?
,应交水费多少元?(3)若有一户居民5月份水费为57.20元,请问该户居民5月份用水多少?
(4)若某户居民6月份、7月份共用水
 ,且6月份水费比7月份水费少12元,则该户居民6、7月份各用水多少?
,且6月份水费比7月份水费少12元,则该户居民6、7月份各用水多少?
【知识点】 分段函数模型的应用
 的边长为2,其中
的边长为2,其中 ,动直线l垂直于边
,动直线l垂直于边 所在的直线,l从点A向右平行移动,交菱形
所在的直线,l从点A向右平行移动,交菱形 于不同的两点P,Q设直线l与点A的距离为x,
于不同的两点P,Q设直线l与点A的距离为x,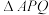 的面积为S,试写出S关于x的函数
的面积为S,试写出S关于x的函数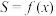 .
.
【知识点】 分段函数模型的应用
 一边靠墙,其他三边用
一边靠墙,其他三边用 长的篱笆围成,设靠墙的一边
长的篱笆围成,设靠墙的一边 的长为
的长为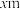 ,花园面积为
,花园面积为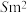 .求
.求 关于
关于 的函数解析式,并求当
的函数解析式,并求当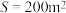 时
时 的值.
的值.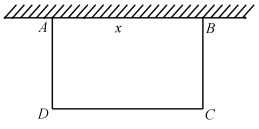
【知识点】 利用二次函数模型解决实际问题
 ),售出商品的数量就增加
),售出商品的数量就增加 成.如果要求该商品的一天营业额至少是10260元,又不能亏本,求x的取值范围.
成.如果要求该商品的一天营业额至少是10260元,又不能亏本,求x的取值范围.
【知识点】 利用二次函数模型解决实际问题 一元二次不等式的实际应用解读
 (百件)时,销售所得的收入为
(百件)时,销售所得的收入为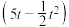 万元.
万元.(Ⅰ)该公司这种产品的年生产量为
 百件,生产并销售这种产品所得到的利润关于当年产量
百件,生产并销售这种产品所得到的利润关于当年产量 的函数为
的函数为 ,求
,求 ;
;(Ⅱ)当该公司的年产量为多少件时,当年所获得的利润最大.
【知识点】 利用二次函数模型解决实际问题 分段函数模型的应用
(1)设一次订购
 件,服装的实际出厂单价为
件,服装的实际出厂单价为 元,写出函数
元,写出函数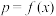 的表达式;
的表达式;(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
【知识点】 分段函数模型的应用 建立拟合函数模型解决实际问题
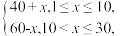 第x天的销售量(单位:件)为g(x)=a-x(a为常数),且在第20天该商品的销售收入为1 200元(销售收入=销售价格×销售量).
第x天的销售量(单位:件)为g(x)=a-x(a为常数),且在第20天该商品的销售收入为1 200元(销售收入=销售价格×销售量).(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
【知识点】 分段函数模型的应用
 (元)与时间
(元)与时间 (天)的函数关系是
(天)的函数关系是 ,该商品的日销售量
,该商品的日销售量 (件)与时间
(件)与时间 (天)的函数关系是
(天)的函数关系是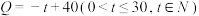 .求这种商品的日销售金额
.求这种商品的日销售金额 的最大值,并指出日销售金额最大的一天是30天中的第几天?(注:日销售金额=日销售价格×日销售量)
的最大值,并指出日销售金额最大的一天是30天中的第几天?(注:日销售金额=日销售价格×日销售量)
【知识点】 利用二次函数模型解决实际问题 分段函数模型的应用
 (
(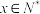 )件.当
)件.当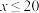 时,年销售总收入为(
时,年销售总收入为(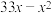 )万元;当
)万元;当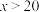 时,年销售总收入为
时,年销售总收入为 万元.记该工厂生产并销售这种产品所得的年利润为
万元.记该工厂生产并销售这种产品所得的年利润为 万元.(年利润=年销售总收入一年总投资)
万元.(年利润=年销售总收入一年总投资)(1)求
 (万元)与
(万元)与 (件)的函数关系式;
(件)的函数关系式;(2)当该工厂的年产量为多少件时,所得年利润最大?最大年利润是多少?
【知识点】 分段函数模型的应用
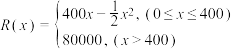 ,其中x是“玉兔”的月产量.
,其中x是“玉兔”的月产量.(1)将利润f(x)表示为月产量x的函数;
(2)当月产量为何值时,该厂所获利润最大?最大利润是多少?(总收益=总成本+利润)
【知识点】 分段函数模型的应用
A,B两城相距100 km,在两地之间距A城x km处的D地建一核电站给A,B两城供电.为保证城市安全,核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城为10亿度/月.
(1)求x的取值范围;
(2)把月供电总费用y表示成x的函数;
(3)核电站建在距A城多远,才能使供电费用最小?
【知识点】 利用二次函数模型解决实际问题
 ,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
【知识点】 利用二次函数模型解决实际问题