12-13高三上·上海·期中
名校
1 . 某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为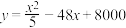 ,已知此生产线年产量最大为
,已知此生产线年产量最大为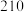 吨.
吨.
(1)求年产量为多少吨时,总成本最低,并求最低成本
(2)若每吨产品平均出厂价为 万元,那么当年产量为多少吨时,可以获得最大利润
万元,那么当年产量为多少吨时,可以获得最大利润 最大利润是多少
最大利润是多少
 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为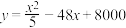 ,已知此生产线年产量最大为
,已知此生产线年产量最大为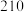 吨.
吨.(1)求年产量为多少吨时,总成本最低,并求最低成本

(2)若每吨产品平均出厂价为
 万元,那么当年产量为多少吨时,可以获得最大利润
万元,那么当年产量为多少吨时,可以获得最大利润 最大利润是多少
最大利润是多少
您最近一年使用:0次
2023-09-07更新
|
724次组卷
|
22卷引用:2015-2016学年江苏省泰兴一中高二下学期期中文科数学试卷
2015-2016学年江苏省泰兴一中高二下学期期中文科数学试卷(已下线)2011-2012学年广东省执信中学高二上学期期末考试理科数学2015-2016学年山东省临沂十八中高二下学期第一次月考文科数学试卷2016-2017学年山西怀仁县一中高二上期开学考理数学试卷2016-2017学年山西怀仁县一中高二上期开学考文数学试卷2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(已下线)学科网2019年高考数学一轮复习讲练测2.9函数模型及其应用【江苏版】 练(已下线)2012届上海市中国中学高三上学期期中考试文科数学试卷(已下线)2015届四川省成都市新都一中高三九月月考文科数学试卷2015-2016学年湖北省孝感六校联盟高一下学期期中考试文科数学卷2015-2016学年河南省新乡延津高中高一下期中数学试卷2015-2016学年湖北省孝感市六校联盟高一下期中理科数学试卷2018届高三数学训练题(14 ):函数模型及其应用 上海市七宝中学2015-2016学年高一上学期期中数学试题山西省晋中市平遥县综合职业技术学校2018-2019学年高三(普通班)上学期期中数学试题山东省临沂第十八中学2024届高三第一次调研考试数学试题河北省承德市第二中学2024届高三上学期开学初摸底数学试题(已下线)高一上学期期中复习【第三章 函数的概念与性质】十大题型归纳(基础篇)-举一反三系列(已下线)第四章 指数函数与对数函数 章末重难点归纳总结-《一隅三反》(已下线)3.4 函数的应用(一)(6大题型)精讲-【题型分类归纳】(人教A版2019必修第一册)宁夏回族自治区银川一中2023-2024学年高一上学期期中考试数学试题上海市上海中学东校2023-2024学年高一上学期期中考试数学试卷
2 . 某企业加工生产一批珠宝,要求每件珠宝都按统一规格加工,每件珠宝的原材料成本为3.5万元,每件珠宝售价(万元)与加工时间 (单位:天)之间的关系满足图1,珠宝的预计销量(件)与加工时间
(单位:天)之间的关系满足图1,珠宝的预计销量(件)与加工时间 (天)之间的关系满足图2.原则上,单件珠宝的加工时间不能超过55天,企业支付的工人报酬为这批珠宝销售毛利润的三分之一,其他成本忽略不计算.
(天)之间的关系满足图2.原则上,单件珠宝的加工时间不能超过55天,企业支付的工人报酬为这批珠宝销售毛利润的三分之一,其他成本忽略不计算.

(1)如果每件珠宝加工天数分别为6,12,预计销量分别会有多少件?
(2)设工厂生产这批珠宝产生的纯利润为 (万元),请写出纯利润
(万元),请写出纯利润 (万元)关于加工时间
(万元)关于加工时间 (天)之间的函数关系式,并求纯利润
(天)之间的函数关系式,并求纯利润 (万元)最大时的预计销量.
(万元)最大时的预计销量.
注:毛利润=总销售额-原材料成本,纯利润=毛利润-工人报酬
 (单位:天)之间的关系满足图1,珠宝的预计销量(件)与加工时间
(单位:天)之间的关系满足图1,珠宝的预计销量(件)与加工时间 (天)之间的关系满足图2.原则上,单件珠宝的加工时间不能超过55天,企业支付的工人报酬为这批珠宝销售毛利润的三分之一,其他成本忽略不计算.
(天)之间的关系满足图2.原则上,单件珠宝的加工时间不能超过55天,企业支付的工人报酬为这批珠宝销售毛利润的三分之一,其他成本忽略不计算.
(1)如果每件珠宝加工天数分别为6,12,预计销量分别会有多少件?
(2)设工厂生产这批珠宝产生的纯利润为
 (万元),请写出纯利润
(万元),请写出纯利润 (万元)关于加工时间
(万元)关于加工时间 (天)之间的函数关系式,并求纯利润
(天)之间的函数关系式,并求纯利润 (万元)最大时的预计销量.
(万元)最大时的预计销量.注:毛利润=总销售额-原材料成本,纯利润=毛利润-工人报酬
您最近一年使用:0次
2019-07-11更新
|
363次组卷
|
2卷引用:江苏省无锡市2018-2019学年高二下学期期末质量数学(文)试题
名校
3 . 新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业A公司扩大生产提供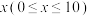 (万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到
(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到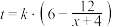 (万件),其中k为工厂工人的复工率(
(万件),其中k为工厂工人的复工率(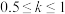 ).A公司生产t万件防护服还需投入成本
).A公司生产t万件防护服还需投入成本 (万元).
(万元).
(1)将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数(政府补贴x万元计入公司收入);
(2)对任意的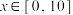 (万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01).
(万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01).
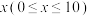 (万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到
(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到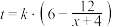 (万件),其中k为工厂工人的复工率(
(万件),其中k为工厂工人的复工率(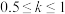 ).A公司生产t万件防护服还需投入成本
).A公司生产t万件防护服还需投入成本 (万元).
(万元).(1)将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数(政府补贴x万元计入公司收入);
(2)对任意的
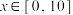 (万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01).
(万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01).
您最近一年使用:0次
2020-10-31更新
|
659次组卷
|
7卷引用:江苏省吴江中学2020-2021学年高二上学期第一次质量检测数学试题
江苏省吴江中学2020-2021学年高二上学期第一次质量检测数学试题安徽省合肥八中2020-2021学年高一上学期10月段考数学试题上海市青浦区2021届高三二模数学试题湖南省岳阳市2020-2021学年高一下学期教学质量检测数学试题(已下线)专题3.8 函数的应用(一)-重难点题型检测-2021-2022学年高一数学举一反三系列(人教A版2019必修第一册)(已下线)专题03 函数的概念与性质(模拟练)-2陕西省西安铁一中学2023-2024学年高一上学期期末考试数学试卷
4 . 新型冠状病毒感染的肺炎治疗过程中,需要某医药公司生产的某种药品.此药品的年固定成本为180万元,每生产 千件需另投入成本为
千件需另投入成本为 .当年产量不足40千件时,
.当年产量不足40千件时, (万元).当年产量不小于40千件时,
(万元).当年产量不小于40千件时,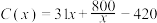 (万元).每千件商品售价为30万元,在疫情期间,该公司生产的药品能全部售完.
(万元).每千件商品售价为30万元,在疫情期间,该公司生产的药品能全部售完.
(1)写出年利润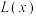 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)该公司决定将此药品所获利润的10%用来捐赠防疫物资.当年产量为多少千件时,在这一药品的生产中所获利润最大?此时可捐赠多少万元的物资款?
 千件需另投入成本为
千件需另投入成本为 .当年产量不足40千件时,
.当年产量不足40千件时, (万元).当年产量不小于40千件时,
(万元).当年产量不小于40千件时,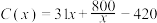 (万元).每千件商品售价为30万元,在疫情期间,该公司生产的药品能全部售完.
(万元).每千件商品售价为30万元,在疫情期间,该公司生产的药品能全部售完.(1)写出年利润
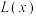 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;(2)该公司决定将此药品所获利润的10%用来捐赠防疫物资.当年产量为多少千件时,在这一药品的生产中所获利润最大?此时可捐赠多少万元的物资款?
您最近一年使用:0次
名校
解题方法
5 . 某工厂某种产品的年固定成本为450万元,每生产 千件,需另投入成本为
千件,需另投入成本为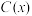 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元),当年产量不小于80千件时,
(万元),当年产量不小于80千件时,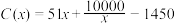 (万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品都能全部售完.
(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品都能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
 千件,需另投入成本为
千件,需另投入成本为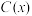 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元),当年产量不小于80千件时,
(万元),当年产量不小于80千件时,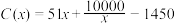 (万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品都能全部售完.
(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品都能全部售完.(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
您最近一年使用:0次
2020-12-25更新
|
159次组卷
|
18卷引用:江苏省徐州市2019-2020学年高二上学期学情调研数学试题
江苏省徐州市2019-2020学年高二上学期学情调研数学试题江苏省苏北地区2019-2020学年高二上学期学情调研数学试题江苏省连云港市赣榆智贤中学2020-2021学年高二上学期9月月考数学试题江西省宜春市宜丰县宜丰中学2019-2020学年高二下学期第一次月考数学(文)试题广东省东莞市光明中学2020-2021学年高二下学期期初考试数学试题江苏省扬州市2022-2023学年高一上学期期末复习数学试题(一)广东省韶关市田家炳中学2020-2021学年高一上学期期中数学试题河北省邯郸市大名一中、磁县一中,邯山区一中,永年一中等六校2020-2021学年高一上学期12月阶段检测数学试题(已下线)3.2.2 基本不等式的应用(练习)-2020-2021学年上学期高一数学同步精品课堂(新教材苏教版必修第一册)广东省韶关市仁化县第一中学2021-2022学年高一上学期第一次月考数学试题广东省广州科学城中学2022-2023学年高一上学期期中数学试题广东省深圳市高级中学2022-2023学年高一上学期期中数学试题山东省青岛市市内四区普通高中2022-2023学年高一上学期期末数学试题湖北省襄阳市第四中学2022-2023学年高一上学期1月阶段性考试数学试题河北省保定市唐县第一中学2022-2023学年高一上学期期中考试数学试题湖南省长沙市实验中学2022-2023学年高一下学期期中数学试题(已下线)人教A版高一上学期【期中押题卷01】-【满分全攻略】(人教A版2019必修第一册)福建省莆田市哲理中学、仙游金石中学2023-2024学年高一上学期期中联考数学试题
6 . 某企业生产一种产品,日销售量 (百件)与产品销售价格
(百件)与产品销售价格 (万元/百件)之间的关系为
(万元/百件)之间的关系为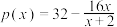 ,已知生产
,已知生产 (百件)该产品所需的成本
(百件)该产品所需的成本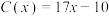 (万元).
(万元).
(1)把该产品每天的利润 表示成日产量
表示成日产量 的函数;
的函数;
(2)求当日产量为多少时,生产该产品每天获得的利润最大?
 (百件)与产品销售价格
(百件)与产品销售价格 (万元/百件)之间的关系为
(万元/百件)之间的关系为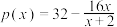 ,已知生产
,已知生产 (百件)该产品所需的成本
(百件)该产品所需的成本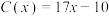 (万元).
(万元).(1)把该产品每天的利润
 表示成日产量
表示成日产量 的函数;
的函数;(2)求当日产量为多少时,生产该产品每天获得的利润最大?
您最近一年使用:0次
名校
7 . 银行按规定每经过一定的时间结算存(贷)款的利息一次,结算后将利息并入本金,这种计算利息的方法叫做复利.现在某企业进行技术改造,有两种方案:
甲方案:一次性向银行贷款10万元,技术改造后第一年可获得利润1万元,以后每年比上年增加30%的利润;
乙方案:每年向银行贷款1万元,技术改造后第一年可获得利润1万元,以后每年比前一年多获利5000元.
(1)设技术改造后,甲方案第n年的利润 为 (万元),乙方案第n年的
(万元),乙方案第n年的利润 为 (万元),请写出
(万元),请写出 、
、 的表达式;
的表达式;
(2)假设两种方案的贷款期限都是10年,到期一次性归还本息.若银行贷款利息均以年息10%的复利计算,试问该企业采用哪种方案获得的扣除本息后的净获利更多?(精确到0.1)(净获利=总利润-本息和)(参考数据 ,
,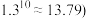
甲方案:一次性向银行贷款10万元,技术改造后第一年可获得利润1万元,以后每年比上年增加30%的利润;
乙方案:每年向银行贷款1万元,技术改造后第一年可获得利润1万元,以后每年比前一年多获利5000元.
(1)设技术改造后,甲方案第n年的
 (万元),乙方案第n年的
(万元),乙方案第n年的 (万元),请写出
(万元),请写出 、
、 的表达式;
的表达式;(2)假设两种方案的贷款期限都是10年,到期一次性归还本息.若银行贷款利息均以年息10%的复利计算,试问该企业采用哪种方案获得的扣除本息后的净获利更多?(精确到0.1)(净获利=总利润-本息和)(参考数据
 ,
,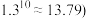
您最近一年使用:0次
2024-06-19更新
|
437次组卷
|
5卷引用:江苏省苏州市苏州大学附属中学2024-2025学年高二上学期10月月考数学试题
江苏省苏州市苏州大学附属中学2024-2025学年高二上学期10月月考数学试题上海市闵行中学2023-2024学年高一下学期期末考试数学试卷(已下线)第13讲 函数的应用(一)-【暑假自学课】(人教A版2019必修第一册)宁夏回族自治区银川一中2024-2025学年高三上学期第一次月考数学试卷(已下线)类型5 以函数的实际应用为背景的解答题(高一期中题型练)
名校
解题方法
8 . 2020年上半年,新冠肺炎疫情在全球蔓延,超过60个国家或地区宣布进入紧急状态,部分国家或地区直接宣布“封国”或“封城”.疫情爆发后,造成医用防护服短缺,某地政府决定为防护服生产企业A公司扩大生产提供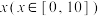 (万元)的专项补贴,并以每套72元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到
(万元)的专项补贴,并以每套72元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到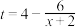 (万套),同时A公司生产t(万套)防护服需要投入成本
(万套),同时A公司生产t(万套)防护服需要投入成本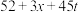 (万元).
(万元).
(1)当政府的专项补贴至少为多少万元时,A公司生产防护服才能不产生亏损?
(2)当政府的专项补贴为多少万元时,A公司生产防护服产生的收益最大?
(注:收益=销售金额+政府专项补贴-成本)
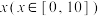 (万元)的专项补贴,并以每套72元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到
(万元)的专项补贴,并以每套72元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到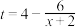 (万套),同时A公司生产t(万套)防护服需要投入成本
(万套),同时A公司生产t(万套)防护服需要投入成本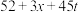 (万元).
(万元).(1)当政府的专项补贴至少为多少万元时,A公司生产防护服才能不产生亏损?
(2)当政府的专项补贴为多少万元时,A公司生产防护服产生的收益最大?
(注:收益=销售金额+政府专项补贴-成本)
您最近一年使用:0次
2020-11-21更新
|
490次组卷
|
4卷引用:江苏省南通市平潮高级中学2020-2021学年高二上学期期中数学试题
名校
9 . 某高科技公司研究开发了一种新产品,生产这种新产品的每天固定成本为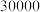 元,每生产
元,每生产 件,需另投入成本为
件,需另投入成本为 元,
元,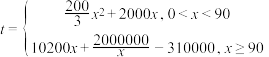 每件产品售价为
每件产品售价为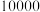 元(该新产品在市场上供不应求可全部卖完).
元(该新产品在市场上供不应求可全部卖完).
(1)写出每天利润 关于每天产量
关于每天产量 的函数解析式;
的函数解析式;
(2)当每天产量为多少件时,该公司在这一新产品的生产中每天所获利润最大.
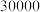 元,每生产
元,每生产 件,需另投入成本为
件,需另投入成本为 元,
元,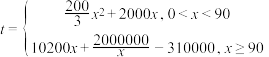 每件产品售价为
每件产品售价为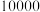 元(该新产品在市场上供不应求可全部卖完).
元(该新产品在市场上供不应求可全部卖完).(1)写出每天利润
 关于每天产量
关于每天产量 的函数解析式;
的函数解析式;(2)当每天产量为多少件时,该公司在这一新产品的生产中每天所获利润最大.
您最近一年使用:0次
2019-10-08更新
|
880次组卷
|
6卷引用:江苏省苏州市外国语学校2019-2020学年上学期自主学习检查(一)高二数学
10 . 某产品拟在2020年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量) 万件与年促销费用
万件与年促销费用 (
(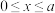 )万元满足
)万元满足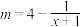 .已知2020年生产该产品的固定投入为8万元,每生产
.已知2020年生产该产品的固定投入为8万元,每生产 万件该产品需要投入25万元.厂家将每件产品的销售价格定为每件产品年平均成本的2倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
万件该产品需要投入25万元.厂家将每件产品的销售价格定为每件产品年平均成本的2倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2020年该产品的利润 万元表示为年促销费用
万元表示为年促销费用 万元的函数;
万元的函数;
(2)该服装厂2020年的促销费用投入多少万元时,利润最大?
 万件与年促销费用
万件与年促销费用 (
(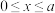 )万元满足
)万元满足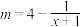 .已知2020年生产该产品的固定投入为8万元,每生产
.已知2020年生产该产品的固定投入为8万元,每生产 万件该产品需要投入25万元.厂家将每件产品的销售价格定为每件产品年平均成本的2倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
万件该产品需要投入25万元.厂家将每件产品的销售价格定为每件产品年平均成本的2倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).(1)将2020年该产品的利润
 万元表示为年促销费用
万元表示为年促销费用 万元的函数;
万元的函数;(2)该服装厂2020年的促销费用投入多少万元时,利润最大?
您最近一年使用:0次



