名校
解题方法
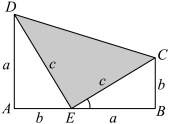
1 . 在如图的直角梯形 中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”.可以简洁明了地推证出勾股定理,把这一证明方法称为“总统证法”.设
中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”.可以简洁明了地推证出勾股定理,把这一证明方法称为“总统证法”.设 ,在梯形
,在梯形 中随机取一点,则此点取自等腰直角
中随机取一点,则此点取自等腰直角 中(阴影部分)的概率是( )
中(阴影部分)的概率是( )
 中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”.可以简洁明了地推证出勾股定理,把这一证明方法称为“总统证法”.设
中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”.可以简洁明了地推证出勾股定理,把这一证明方法称为“总统证法”.设 ,在梯形
,在梯形 中随机取一点,则此点取自等腰直角
中随机取一点,则此点取自等腰直角 中(阴影部分)的概率是( )
中(阴影部分)的概率是( )
A. | B. | C. | D. |
您最近一年使用:0次
名校
2 . “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用形数结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角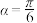 ,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )
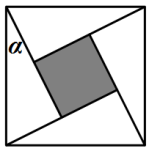
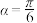 ,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )
A. | B. | C.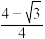 | D. |
您最近一年使用:0次
2020-10-23更新
|
646次组卷
|
27卷引用:2017届重庆巴蜀中学高三文12月月考数学试卷
2017届重庆巴蜀中学高三文12月月考数学试卷吉林省吉林大学附属中学2017届高三第五次摸底考试数学(理)试题湖北省襄阳市第四中学2017届高三下学期第一次模拟考试数学(理)试题四川省南充高级中学2018届高三9月检测数学(文)试题湖南省长沙市长郡中学2018届高三月考试题(二)数学(理科)试题安徽省芜湖市2018届高三上学期期末考试(一模)理科数学试题东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)2018届高三第二次模拟考试数学(文)试题【市级联考】四川省广元市2019届高三第一次高考适应性统考数学试题(理工类)【全国百强校】北京市人大附中2019届高三高考模拟预测考试一数学试题【校级联考】闽粤赣三省十校2019届高三下学期联考数学(文)试题2019届湖北省黄冈中学、华师一附中、襄阳四中、襄阳五中、荆州中学等八校高三第二次联考数学(理)试题江西省新余市第四中学2021届高三上学期第一次段考数学(理)试题福建省莆田第十五中学2019届高三上学期期中考试数学理科试题(已下线)专题12 几何概型(客观题)-2021年高考数学(理)二轮复习热点题型精选精练(已下线)专题12 几何概型(客观题)-2021年高考数学(文)二轮复习热点题型精选精练(已下线)专题11 几何概型(客观题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)陕西省西安市铁一中学2020-2021学年高三上学期第四次月考理科数学试题山东省烟台市2016-2017学年高一下学期期中考试数学试题广东省韶关市2016-2017学年高一下学期期末考试数学试题河南省商丘市第一高级中学2017-2018学年高二10月月考数学(文)试题河南省商丘市第一高级中学2017-2018学年高二10月月考数学(理)试题广东清远市2017-2018学年高二第一学期末质量检测理科数学试题辽宁省六校协作体2017-2018学年高二下学期期中考试数学(文)试卷【全国百强校】黑龙江省鹤岗市第一中学2018-2019学年高二下学期第二次月考数学(理)试题河南省郑州市四中2017-2018学年高一下学期第一次月考数学试题广东省广州市天河区2018-2019学年高二上学期期末数学(理)试题湖南省长沙市雨花区2017-2018学年高一下学期期末数学试题
名校
3 . 经数学家证明:“在平面上画有一组间距为a的平行线,将一根长度为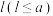 的针任意掷在这个平面上,此针与平行线中任一条相交的概率为
的针任意掷在这个平面上,此针与平行线中任一条相交的概率为 (其中
(其中 为圆周率)”某试验者用一根长度为2cm的针,在画有一组间距为3cm平行线所在的平面上投掷了n次,其中有120次出现该针与平行线相交,并据此估算出
为圆周率)”某试验者用一根长度为2cm的针,在画有一组间距为3cm平行线所在的平面上投掷了n次,其中有120次出现该针与平行线相交,并据此估算出 的近似值为
的近似值为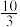 ,则
,则 ( )
( )
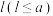 的针任意掷在这个平面上,此针与平行线中任一条相交的概率为
的针任意掷在这个平面上,此针与平行线中任一条相交的概率为 (其中
(其中 为圆周率)”某试验者用一根长度为2cm的针,在画有一组间距为3cm平行线所在的平面上投掷了n次,其中有120次出现该针与平行线相交,并据此估算出
为圆周率)”某试验者用一根长度为2cm的针,在画有一组间距为3cm平行线所在的平面上投掷了n次,其中有120次出现该针与平行线相交,并据此估算出 的近似值为
的近似值为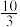 ,则
,则 ( )
( )| A.300 | B.400 | C.500 | D.600 |
您最近一年使用:0次
2021-03-01更新
|
437次组卷
|
7卷引用:黑龙江省哈尔滨九中2021届高三五模数学(文)试题
解题方法
4 . 我国古代数学家赵爽在为《周髀算经》一书作序时,介绍了“勾股圆方图”(亦称“赵爽弦图”),弦图用数形结合的方式证明了勾股定理,他比希腊数学家毕达哥拉斯证明该定理要早500多年.类比赵爽的弦图,可构造如图所示的图形,将一个大等边三角形分成三个全等三角形与中间的一个小等边三角形.设 ,若在大等边三角形内取一点P,则该点取自小等边三角形内部的概率为( )
,若在大等边三角形内取一点P,则该点取自小等边三角形内部的概率为( )
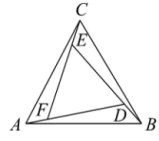
 ,若在大等边三角形内取一点P,则该点取自小等边三角形内部的概率为( )
,若在大等边三角形内取一点P,则该点取自小等边三角形内部的概率为( )
A.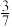 | B. | C. | D. |
您最近一年使用:0次
解题方法
5 . 如图是汉代数学家赵爽在注解《周髀算经》时绘制的“赵爽弦图”,该图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形,这是我国对勾股定理的最早证明.记直角三角形中较小的锐角为 ,且
,且 .若在大正方形内随机取一点,则此点取自小正方形的概率是( )
.若在大正方形内随机取一点,则此点取自小正方形的概率是( )

 ,且
,且 .若在大正方形内随机取一点,则此点取自小正方形的概率是( )
.若在大正方形内随机取一点,则此点取自小正方形的概率是( )
A. | B.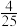 | C. | D. |
您最近一年使用:0次
2020-05-14更新
|
191次组卷
|
2卷引用:2020届安徽省示范高中皖北协作区高三下学期第22届联考理科数学试题
名校
解题方法
6 . “勾股定理”在西方被称为“毕达哥拉斯定理”.三国时期,吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形中较小的锐角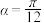 ,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
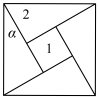
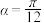 ,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
| A.30 | B.40 | C.50 | D.60 |
您最近一年使用:0次
2020-04-11更新
|
408次组卷
|
3卷引用:湖湘名校(A佳教育)2019-2020学年高三下学期3月线上自主联合检测数学(理)试题
名校
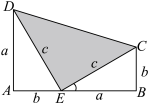
7 . 1876年4月1日,加菲尔德在《新英格兰教育日志》上发表了勾股定理的一种证明方法,即在如图的直角梯形 中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”,可以简洁明了地推证出勾股定理.1881年加菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、易懂的证明,就把这一证明方法称为“总统证法”.如图,设
中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”,可以简洁明了地推证出勾股定理.1881年加菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、易懂的证明,就把这一证明方法称为“总统证法”.如图,设 ,在梯形
,在梯形 中随机取一点,则此点取自等腰直角
中随机取一点,则此点取自等腰直角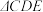 中(阴影部分)的概率是
中(阴影部分)的概率是
 中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”,可以简洁明了地推证出勾股定理.1881年加菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、易懂的证明,就把这一证明方法称为“总统证法”.如图,设
中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”,可以简洁明了地推证出勾股定理.1881年加菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、易懂的证明,就把这一证明方法称为“总统证法”.如图,设 ,在梯形
,在梯形 中随机取一点,则此点取自等腰直角
中随机取一点,则此点取自等腰直角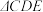 中(阴影部分)的概率是
中(阴影部分)的概率是
A. | B. | C. | D. |
您最近一年使用:0次
2019-06-18更新
|
504次组卷
|
5卷引用:【校级联考】晋冀鲁豫中原名校2019届高三第三次联考数学(文)试题
名校
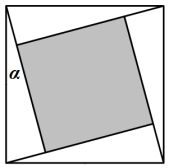
8 . “勾股定理”在西方被称为“毕达哥拉斯定理”,国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明 如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形
如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形 若直角三角形中较小的锐角
若直角三角形中较小的锐角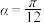 ,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是
,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是

 如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形
如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形 若直角三角形中较小的锐角
若直角三角形中较小的锐角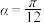 ,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是
,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是


A. | B. | C.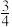 | D.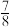 |
您最近一年使用:0次
2019-04-20更新
|
372次组卷
|
5卷引用:【全国百强校】宁夏平罗中学 2019 届高三第二次模拟考试理科数学试题
名校
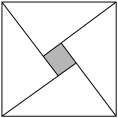
9 . “勾股圆方图”是我国古代数学家赵爽设计的一幅用来证明勾股定理的图案,如图所示.在“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形.若直角三角形中较小的锐角 满足
满足 ,则从图中随机取一点,则此点落在阴影部分的概率是
,则从图中随机取一点,则此点落在阴影部分的概率是
 满足
满足 ,则从图中随机取一点,则此点落在阴影部分的概率是
,则从图中随机取一点,则此点落在阴影部分的概率是
A.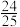 | B. | C.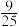 | D. |
您最近一年使用:0次
2019-04-02更新
|
424次组卷
|
3卷引用:【市级联考】安徽省安庆市2019届高三模拟考试(二模)数学文试题
名校
10 . 四色猜想是世界三大数学猜想之一,1976年数学家阿佩尔与哈肯证明,称为四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用 ,
, ,
, ,
, 四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为
四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为 ,粗实线围成的各区域上分别标有数字
,粗实线围成的各区域上分别标有数字 ,
, ,
, ,
, 的四色地图符合四色定理,区域
的四色地图符合四色定理,区域 和区域
和区域 标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为
标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为 的区域的概率所有可能值中,最大的是
的区域的概率所有可能值中,最大的是

 ,
, ,
, ,
, 四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为
四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为 ,粗实线围成的各区域上分别标有数字
,粗实线围成的各区域上分别标有数字 ,
, ,
, ,
, 的四色地图符合四色定理,区域
的四色地图符合四色定理,区域 和区域
和区域 标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为
标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为 的区域的概率所有可能值中,最大的是
的区域的概率所有可能值中,最大的是
A. | B. | C. | D. |
您最近一年使用:0次
2019-01-21更新
|
833次组卷
|
7卷引用:【市级联考】山东省潍坊市2019届高三上学期期末测试数学(文科)试题



