名校
解题方法
1 . 对于正实数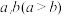 有基本不等式:
有基本不等式: ,其中
,其中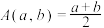 ,为
,为 的算术平均数,
的算术平均数,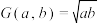 ,为
,为 的几何平均数.现定义
的几何平均数.现定义 的对数平均数:
的对数平均数:
(1)设 ,求证:
,求证: :
:
(2)①证明不等式: :
:
②若不等式 对于任意的正实数
对于任意的正实数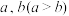 恒成立,求正实数
恒成立,求正实数 的最大值.
的最大值.
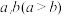 有基本不等式:
有基本不等式: ,其中
,其中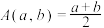 ,为
,为 的算术平均数,
的算术平均数,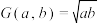 ,为
,为 的几何平均数.现定义
的几何平均数.现定义 的对数平均数:
的对数平均数:
(1)设
 ,求证:
,求证: :
:(2)①证明不等式:
 :
:②若不等式
 对于任意的正实数
对于任意的正实数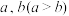 恒成立,求正实数
恒成立,求正实数 的最大值.
的最大值.
您最近一年使用:0次
2022-05-11更新
|
490次组卷
|
6卷引用:湖北省十一校2022届高三下学期第二次联考数学试题
名校
解题方法
2 . 基本不等式可以推广到一般的情形:对于 个正数
个正数 ,它们的算术平均不小于它们的几何平均,即
,它们的算术平均不小于它们的几何平均,即 ,当且仅当
,当且仅当 时,等号成立.若无穷正项数列
时,等号成立.若无穷正项数列 同时满足下列两个性质:①
同时满足下列两个性质:①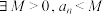 ;②
;② 为单调数列,则称数列
为单调数列,则称数列 具有性质
具有性质 .
.
(1)若 ,求数列
,求数列 的最小项;
的最小项;
(2)若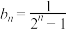 ,记
,记 ,判断数列
,判断数列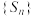 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(3)若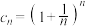 ,求证:数列
,求证:数列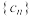 具有性质
具有性质 .
.
 个正数
个正数 ,它们的算术平均不小于它们的几何平均,即
,它们的算术平均不小于它们的几何平均,即 ,当且仅当
,当且仅当 时,等号成立.若无穷正项数列
时,等号成立.若无穷正项数列 同时满足下列两个性质:①
同时满足下列两个性质:①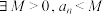 ;②
;② 为单调数列,则称数列
为单调数列,则称数列 具有性质
具有性质 .
.(1)若
 ,求数列
,求数列 的最小项;
的最小项;(2)若
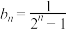 ,记
,记 ,判断数列
,判断数列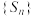 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;(3)若
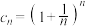 ,求证:数列
,求证:数列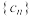 具有性质
具有性质 .
.
您最近一年使用:0次
2024-02-21更新
|
3096次组卷
|
6卷引用:湖北省荆州市沙市中学2024届高三下学期3月月考数学试题
湖北省荆州市沙市中学2024届高三下学期3月月考数学试题安徽省部分省示范高中2024届高三开学联考数学试卷湖南省2024年高三数学新改革提高训练三(九省联考题型)(已下线)黄金卷04(2024新题型)广东省广州市西关外国语学校2023-2024学年高二下学期期中数学试题(已下线)压轴题03不等式压轴题13题型汇总-2
名校
3 . 向量外积(又称叉积)广泛应用于物理与数学领域.定义两个向量 与
与 的叉积
的叉积 ,规定
,规定 的模长为
的模长为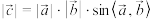 ,
, 与
与 、
、 所在平面垂直,其方向满足如图1所示规则,且须满足如图所示的排列顺序.已知向量外积满足分配律,且
所在平面垂直,其方向满足如图1所示规则,且须满足如图所示的排列顺序.已知向量外积满足分配律,且 .
.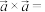 ;②
;②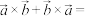 ;
;
(2)空间直角坐标系中有向量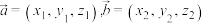 ,
,
①若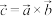 ,用含
,用含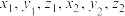 的坐标表示
的坐标表示 ;
;
② 证明:
证明: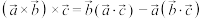 ;
;
(3)如图2所示,平面直角坐标系 中有三角形OAB,
中有三角形OAB, ,试探究
,试探究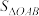 的表达式.
的表达式.
 与
与 的叉积
的叉积 ,规定
,规定 的模长为
的模长为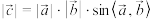 ,
, 与
与 、
、 所在平面垂直,其方向满足如图1所示规则,且须满足如图所示的排列顺序.已知向量外积满足分配律,且
所在平面垂直,其方向满足如图1所示规则,且须满足如图所示的排列顺序.已知向量外积满足分配律,且 .
.
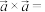 ;②
;②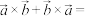 ;
;(2)空间直角坐标系中有向量
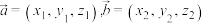 ,
,①若
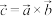 ,用含
,用含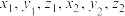 的坐标表示
的坐标表示 ;
;②
 证明:
证明: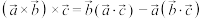 ;
;(3)如图2所示,平面直角坐标系
 中有三角形OAB,
中有三角形OAB, ,试探究
,试探究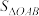 的表达式.
的表达式.
您最近一年使用:0次
名校
解题方法
4 . 给出下列两个定义:
I.对于函数 ,定义域为
,定义域为 ,且其在
,且其在 上是可导的,若其导函数定义域也为
上是可导的,若其导函数定义域也为 ,则称该函数是“同定义函数”.
,则称该函数是“同定义函数”.
II.对于一个“同定义函数” ,若有以下性质:
,若有以下性质:
①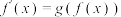 ;②
;②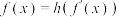 ,其中
,其中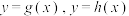 为两个新的函数,
为两个新的函数, 是
是 的导函数.
的导函数.
我们将具有其中一个性质的函数 称之为“单向导函数”,将两个性质都具有的函数
称之为“单向导函数”,将两个性质都具有的函数 称之为“双向导函数”,将
称之为“双向导函数”,将 称之为“自导函数”.
称之为“自导函数”.
(1)判断函数 和
和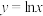 是“单向导函数”,或者“双向导函数”,说明理由.如果具有性质①,则写出其对应的“自导函数”;
是“单向导函数”,或者“双向导函数”,说明理由.如果具有性质①,则写出其对应的“自导函数”;
(2)已知命题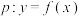 是“双向导函数”且其“自导函数”为常值函数,命题
是“双向导函数”且其“自导函数”为常值函数,命题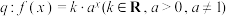 .判断命题
.判断命题 是
是 的什么条件,证明你的结论;
的什么条件,证明你的结论;
(3)已知函数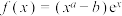 .
.
①若 的“自导函数”是
的“自导函数”是 ,试求
,试求 的取值范围;
的取值范围;
②若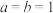 ,且定义
,且定义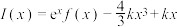 ,若对任意
,若对任意 ,不等式
,不等式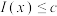 恒成立,求
恒成立,求 的取值范围.
的取值范围.
I.对于函数
 ,定义域为
,定义域为 ,且其在
,且其在 上是可导的,若其导函数定义域也为
上是可导的,若其导函数定义域也为 ,则称该函数是“同定义函数”.
,则称该函数是“同定义函数”.II.对于一个“同定义函数”
 ,若有以下性质:
,若有以下性质:①
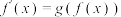 ;②
;②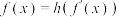 ,其中
,其中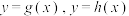 为两个新的函数,
为两个新的函数, 是
是 的导函数.
的导函数.我们将具有其中一个性质的函数
 称之为“单向导函数”,将两个性质都具有的函数
称之为“单向导函数”,将两个性质都具有的函数 称之为“双向导函数”,将
称之为“双向导函数”,将 称之为“自导函数”.
称之为“自导函数”.(1)判断函数
 和
和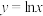 是“单向导函数”,或者“双向导函数”,说明理由.如果具有性质①,则写出其对应的“自导函数”;
是“单向导函数”,或者“双向导函数”,说明理由.如果具有性质①,则写出其对应的“自导函数”;(2)已知命题
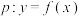 是“双向导函数”且其“自导函数”为常值函数,命题
是“双向导函数”且其“自导函数”为常值函数,命题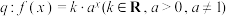 .判断命题
.判断命题 是
是 的什么条件,证明你的结论;
的什么条件,证明你的结论;(3)已知函数
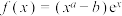 .
.①若
 的“自导函数”是
的“自导函数”是 ,试求
,试求 的取值范围;
的取值范围;②若
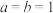 ,且定义
,且定义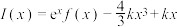 ,若对任意
,若对任意 ,不等式
,不等式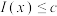 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-02-20更新
|
2461次组卷
|
10卷引用:湖北省武昌实验中学2023-2024学年高二下学期三月月考数学试卷
湖北省武昌实验中学2023-2024学年高二下学期三月月考数学试卷上海市普陀区桃浦中学2022-2023学年高二上学期12月月考数学试题上海市普陀区桃浦中学2022-2023学年高二上学期10月月考数学试题湖南省长沙市雅礼中学2024届高三月考试卷数学(六)浙江省湖州市第二中学2024届高三下学期新高考模拟数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编2024届高三新改革适应性模拟测试数学试卷四(九省联考题型)辽宁省沈阳市东北育才学校科学高中部2023-2024学年高三下学期第六次模拟考试数学试卷(已下线)上海市奉贤区2024届高三一模数学试题变式题16-21
解题方法
5 . 对于函数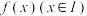 ,若存在非零常数M,使得对任意的
,若存在非零常数M,使得对任意的 ,都有
,都有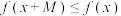 成立,我们称函数
成立,我们称函数 为“M函数”;对于函数
为“M函数”;对于函数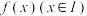 ,若存在非零常数M,使得对任意的
,若存在非零常数M,使得对任意的 ,都有
,都有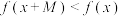 成立,我们称函数
成立,我们称函数 为“严格M函数”.
为“严格M函数”.
(1)求证: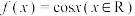 ,是“M函数”;
,是“M函数”;
(2)若函数 ,是“
,是“ 函数”,求k的取值范围;
函数”,求k的取值范围;
(3)对于定义域为R的函数 对任意的正实数M,
对任意的正实数M, 均是“严格M函数”,若
均是“严格M函数”,若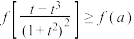 ,求实数a的最小值.
,求实数a的最小值.
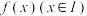 ,若存在非零常数M,使得对任意的
,若存在非零常数M,使得对任意的 ,都有
,都有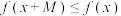 成立,我们称函数
成立,我们称函数 为“M函数”;对于函数
为“M函数”;对于函数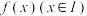 ,若存在非零常数M,使得对任意的
,若存在非零常数M,使得对任意的 ,都有
,都有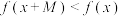 成立,我们称函数
成立,我们称函数 为“严格M函数”.
为“严格M函数”.(1)求证:
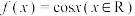 ,是“M函数”;
,是“M函数”;(2)若函数
 ,是“
,是“ 函数”,求k的取值范围;
函数”,求k的取值范围;(3)对于定义域为R的函数
 对任意的正实数M,
对任意的正实数M, 均是“严格M函数”,若
均是“严格M函数”,若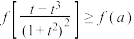 ,求实数a的最小值.
,求实数a的最小值.
您最近一年使用:0次
2023-04-30更新
|
378次组卷
|
2卷引用:湖北省襄阳市第三中学2022-2023学年高一下学期5月月考数学试题
解题方法
6 . 若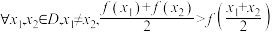 ,则称
,则称 在区间
在区间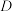 上的图象是凹的;若
上的图象是凹的;若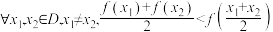 ,则称
,则称 在区间
在区间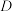 上的图象是凸的.
上的图象是凸的.
(1)判断函数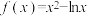 在区间
在区间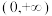 上的图象是凹的还是凸的,根据凹凸性的定义证明你的结论;
上的图象是凹的还是凸的,根据凹凸性的定义证明你的结论;
(2)判断函数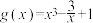 在区间
在区间 上的图象是凹的还是凸的,根据凹凸性的定义证明你的结论.
上的图象是凹的还是凸的,根据凹凸性的定义证明你的结论.
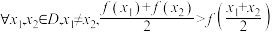 ,则称
,则称 在区间
在区间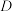 上的图象是凹的;若
上的图象是凹的;若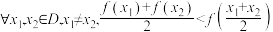 ,则称
,则称 在区间
在区间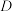 上的图象是凸的.
上的图象是凸的.(1)判断函数
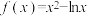 在区间
在区间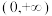 上的图象是凹的还是凸的,根据凹凸性的定义证明你的结论;
上的图象是凹的还是凸的,根据凹凸性的定义证明你的结论;(2)判断函数
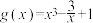 在区间
在区间 上的图象是凹的还是凸的,根据凹凸性的定义证明你的结论.
上的图象是凹的还是凸的,根据凹凸性的定义证明你的结论.
您最近一年使用:0次
2022-10-11更新
|
620次组卷
|
3卷引用:湖北省百校2022-2023学年高三上学期10月联考数学试题
湖北省百校2022-2023学年高三上学期10月联考数学试题辽宁省葫芦岛市协作校2022-2023学年高三上学期第一次考试数学试题(已下线)第一章 导数与函数的图像 专题二 函数的凹凸性与渐近线 微点1 函数的凹凸性与渐近线
名校
解题方法
7 . 对在直角坐标系的第一象限内的任意两点作如下定义:若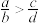 ,那么称点
,那么称点 是点
是点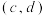 的“上位点”.同时点
的“上位点”.同时点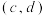 是点
是点 的“下位点”;
的“下位点”;
(1)试写出点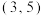 的一个“上位点”坐标和一个“下位点”坐标;
的一个“上位点”坐标和一个“下位点”坐标;
(2)已知点 是点
是点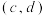 的“上位点”,判断点
的“上位点”,判断点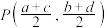 是否是点
是否是点 的“下位点”,证明你的结论;
的“下位点”,证明你的结论;
(3)设正整数 满足以下条件:对集合
满足以下条件:对集合 内的任意元素
内的任意元素 ,总存在正整数
,总存在正整数 ,使得点
,使得点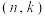 既是点
既是点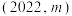 的“下位点”,又是点
的“下位点”,又是点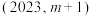 的“上位点”,求满足要求的一个正整数
的“上位点”,求满足要求的一个正整数 的值,并说明理由.
的值,并说明理由.
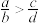 ,那么称点
,那么称点 是点
是点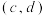 的“上位点”.同时点
的“上位点”.同时点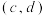 是点
是点 的“下位点”;
的“下位点”;(1)试写出点
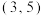 的一个“上位点”坐标和一个“下位点”坐标;
的一个“上位点”坐标和一个“下位点”坐标;(2)已知点
 是点
是点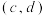 的“上位点”,判断点
的“上位点”,判断点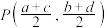 是否是点
是否是点 的“下位点”,证明你的结论;
的“下位点”,证明你的结论;(3)设正整数
 满足以下条件:对集合
满足以下条件:对集合 内的任意元素
内的任意元素 ,总存在正整数
,总存在正整数 ,使得点
,使得点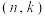 既是点
既是点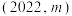 的“下位点”,又是点
的“下位点”,又是点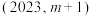 的“上位点”,求满足要求的一个正整数
的“上位点”,求满足要求的一个正整数 的值,并说明理由.
的值,并说明理由.
您最近一年使用:0次
2022-11-11更新
|
777次组卷
|
14卷引用:湖北省襄阳市第四中学2023-2024学年高一上学期9月月考数学试题
湖北省襄阳市第四中学2023-2024学年高一上学期9月月考数学试题上海市闵行中学、文绮中学2022-2023学年高一上学期期中数学试题北京市大兴区2022-2023学年高一上学期期末考试数学试题(已下线)1.1集合的概念(分层作业)-【上好课】(已下线)高一上学期第一次月考解答题压轴题50题专练-举一反三系列(已下线)高一上学期期中考试解答题压轴题50题专练-举一反三系列上海市复兴高级中学2023-2024学年高一上学期10月月考数学试题(已下线)专题01集合及其表示方法1-【倍速学习法】(沪教版2020必修第一册)(已下线)期中真题必刷压轴30题-【满分全攻略】(沪教版2020必修第一册)(已下线)期中真题必刷压轴60题(15个考点专练)-【满分全攻略】(人教A版2019必修第一册)江苏省苏州市苏州高新区一中2023-2024学年高一上学期10月月考数学试题(已下线)期末真题必刷压轴60题(10个考点专练)-【满分全攻略】(沪教版2020必修第一册)(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】(人教A版2019必修第一册)(已下线)专题06 信息迁移型【练】【北京版】
名校
解题方法
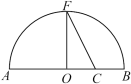
8 . 《几何原本》卷 的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,运用这一原理,很多代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点
的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,运用这一原理,很多代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点 在半圆
在半圆 上,点
上,点 在直径
在直径 上,且
上,且 ,设
,设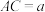 ,
, ,则该图形可以完成的无字证明为( )
,则该图形可以完成的无字证明为( )
 的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,运用这一原理,很多代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点
的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,运用这一原理,很多代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点 在半圆
在半圆 上,点
上,点 在直径
在直径 上,且
上,且 ,设
,设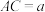 ,
, ,则该图形可以完成的无字证明为( )
,则该图形可以完成的无字证明为( )
A.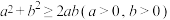 | B.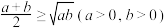 |
C.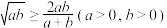 | D.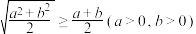 |
您最近一年使用:0次
2022-10-28更新
|
754次组卷
|
63卷引用:湖北省荆州市沙市中学2021-2022学年高一上学期期中数学试题
湖北省荆州市沙市中学2021-2022学年高一上学期期中数学试题湖北省武汉市第六中学2022-2023学年高一上学期第一次月考数学试题湖北省武汉市部分重点中学2022-2023学年高一上学期10月联考数学试题河北省衡水中学2017届高三高考押题理数试题安徽省巢湖市柘皋中学2017届高三最后一次模拟考试数学(理)试题安徽省巢湖市柘皋中学2017届高三最后一次模拟考试数学(文)试题河北省衡水中学2017届高三押题卷(I卷)文数试题【全国百强校】河北省衡水中学2018届高三高考押题(一)文数试题【全国百强校】河北省衡水中学2018届高三高考押题(一)理数试题河北省衡水中学2018年高考押题(一)文科数学河北省衡水中学2018年高考押题(一)理科数学【市级联考】山东省枣庄市2018-2019学年高二上学期期末第二学段模块考试数学试题2020届山东省潍坊市高三下学期开学考试数学试题2020届陕西省西安市西北工业大学附中高三第一次模拟考试数学(文)试题(已下线)备战2020年高考数学之考场再现(山东专版)05(已下线)第2篇——相等关系与不等关系,计数原理-新高考山东专题汇编(已下线)2.2基本不等式-2020-2021学年新教材名师导学导练高中数学必修第一册(人教A版)福建省莆田第一中学2019-2020学年高一下学期期末考试数学试题(已下线)考点06 基本不等式(考点专练)-备战2021年新高考数学一轮复习考点微专题陕西省西北工业大学附属中学2019届高三下学期模拟训练(4)数学(理)试题(已下线)专题7.3 基本不等式-2021年高考数学(文)一轮复习-题型全归纳与高效训练突破广东省汕头市陈店实验学校2020-2021学年高一上学期第一次月考数学试题广东省中山市一中2020-2021学年高一上学期第一次段考数学试题第二章+等式与不等式(基础过关)-2020-2021学年高一数学单元测试定心卷(人教B版2019必修第一册)安徽省亳州市第三十二中学2020-2021学年高一上学期第一次月考数学试题江苏省无锡市江阴二中、要塞中学等四校2020-2021学年高二上学期期中数学试题(已下线)专题7.3 基本不等式 (精练)-2021届高考数学复习(理)一轮讲练测广东省深圳市部分学校2020-2021学年高一上数学期中试题江苏省淮安市六校(金湖中学、洪泽中学等)2020-2021学年高二上学期第二次联考(期中)数学试题(已下线)专题08 基本不等式(客观题)-2021年高考数学(理)二轮复习热点题型精选精练(已下线)专题08 基本不等式(客观题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)(已下线)专题08 基本不等式(客观题)-2021年高考数学(文)二轮复习热点题型精选精练新疆巴音郭楞蒙古自治州第二中学2021届高三上学期第二次摸底考试数学(文)试题新疆巴音郭楞蒙古自治州第二中学2021届高三上学期第二次摸底考试数学(理)试题福建省泉州晋江市磁灶中学、内坑中学2021届高三上学期期末联考数学试题江苏省淮安市六校(洪泽中学、金湖中学等)2020-2021学年高二上学期第二次联考数学试题宁夏银川一中2020-2021学年高一下学期期末数学试题江苏省淮安市涟水中学2020-2021学年高二上学期期中数学试题2.2基本不等式(课前预习+课堂探究)-2021-2022学年高一数学课堂精选(人教A版2019必修第一册)(已下线)第二章 一元二次函数、方程和不等式(B卷)-2021-2022学年高中数学必修第一册课时解读与训练(人教A版2019)浙江省宁波市咸祥中学2020-2021学年高二下学期期中数学试题(已下线)考点26 基本不等式-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)“8+4+4”小题强化训练(15)不等式的综合应用-2022届高考数学一轮复习(江苏等新高考地区专用)河南省焦作市温县第一高级中学2021-2022学年高一上学期9月月考数学试题辽宁省沈阳二中2021-2022学年高一10月份月考数学试题福建省泉州泉州第一中学2020-2021学年高一上学期期中考试数学试题(已下线)2.2.1基本不等式-【新教材】人教A版(2019)高中数学必修第一册同步练习江苏省徐州市2021-2022学年高一上学期期中数学试题辽宁省沈阳市第二中学2021-2022学年高一上学期第一次月考数学试题(已下线)专题03 与基本不等式相关的情景化试题 - 2021-2022学年高一数学新教材情境化新题(人教A版2019必修第一册) (已下线)第三章 不等式(提分小卷)-【单元测试】2021-2022学年高一数学尖子生选拔卷(苏教版2019必修第一册)(已下线)专题9.1 期中押题检测卷(考试范围:第1-4章) 1(易)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(苏教版2019必修第一册)(已下线)专题2.2 基本不等式-《讲亮点》2021-2022学年高一数学新教材同步配套讲练(人教A版2019必修第一册)(已下线)第08讲 基本不等式-【暑假自学课】2022年新高一数学暑假精品课(苏教版2019必修第一册)(已下线)2.2基本不等式A卷(已下线)突破2.2 基本不等式(课时训练)辽宁省大连市第二十高级中学2022-2023学年高一上学期10月月考数学试题江苏省常州市横林高级中学2022-2023学年高一上学期10月阶段性测试数学试题江苏省盐城市响水县灌江高级中学2022-2023学年高一上学期学情分析考试数学试题沪教版(2020) 必修第一册 单元训练 第2章 基本不等式及其应用(A卷)福建省南安市蓝园高级中学2022-2023学年高一上学期9月学情检测数学试题宁夏银川市贺兰县景博中学2022-2023学年高二上学期期中考试数学试题(理)内蒙古赤峰二中2023-2024学年高一上学期第一次月考数学试题
真题
名校
9 . 已知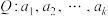 为有穷整数数列.给定正整数m,若对任意的
为有穷整数数列.给定正整数m,若对任意的 ,在Q中存在
,在Q中存在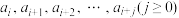 ,使得
,使得 ,则称Q为
,则称Q为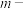 连续可表数列.
连续可表数列.
(1)判断 是否为
是否为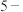 连续可表数列?是否为
连续可表数列?是否为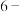 连续可表数列?说明理由;
连续可表数列?说明理由;
(2)若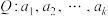 为
为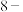 连续可表数列,求证:k的最小值为4;
连续可表数列,求证:k的最小值为4;
(3)若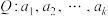 为
为 连续可表数列,且
连续可表数列,且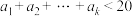 ,求证:
,求证: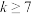 .
.
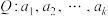 为有穷整数数列.给定正整数m,若对任意的
为有穷整数数列.给定正整数m,若对任意的 ,在Q中存在
,在Q中存在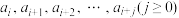 ,使得
,使得 ,则称Q为
,则称Q为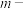 连续可表数列.
连续可表数列.(1)判断
 是否为
是否为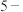 连续可表数列?是否为
连续可表数列?是否为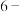 连续可表数列?说明理由;
连续可表数列?说明理由;(2)若
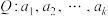 为
为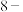 连续可表数列,求证:k的最小值为4;
连续可表数列,求证:k的最小值为4;(3)若
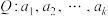 为
为 连续可表数列,且
连续可表数列,且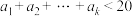 ,求证:
,求证: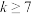 .
.
您最近一年使用:0次
2022-06-07更新
|
11329次组卷
|
13卷引用:湖北省黄冈市浠水县第一中学2024届高三下学期第四次高考模拟数学试题
湖北省黄冈市浠水县第一中学2024届高三下学期第四次高考模拟数学试题2022年新高考北京数学高考真题(已下线)2022年新高考北京数学高考真题变式题13-15题北京市第二十二中学2023届高三上学期开学考试数学试题(已下线)2022年新高考北京数学高考真题变式题19-21题(已下线)重组卷02(已下线)专题16 数列新定义题的解法 微点2 数列新定义题的解法(二)北京十年真题专题06数列(已下线)数列新定义(已下线)重难点10 数列的通项、求和及综合应用【九大题型】(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)(已下线)专题21 数列解答题(理科)-4(已下线)专题21 数列解答题(文科)-2
10 . 将有穷数列 中部分项按原顺序构成的新数列
中部分项按原顺序构成的新数列 称为
称为 的一个“子列”,剩余项按原顺序构成“子列”
的一个“子列”,剩余项按原顺序构成“子列” .若{bn}各项的和与
.若{bn}各项的和与 各项的和相等,则称
各项的和相等,则称 和
和 为数列
为数列 的一对“完美互补子列”.
的一对“完美互补子列”.
(1)若数列 为
为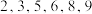 ,请问
,请问 是否存在“完美互补子列”?并说明理由;
是否存在“完美互补子列”?并说明理由;
(2)已知共100项的等比数列 为递减数列,且
为递减数列,且 ,公比为q.若
,公比为q.若 存在“完美互补子列”,求证:
存在“完美互补子列”,求证: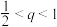 ;
;
(3)数列 满足
满足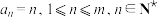 .设
.设 共有
共有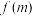 对“完美互补子列”,求证:当
对“完美互补子列”,求证:当 和
和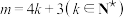 时,
时, 都存在“完美互补子列”且
都存在“完美互补子列”且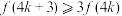 .
.
 中部分项按原顺序构成的新数列
中部分项按原顺序构成的新数列 称为
称为 的一个“子列”,剩余项按原顺序构成“子列”
的一个“子列”,剩余项按原顺序构成“子列” .若{bn}各项的和与
.若{bn}各项的和与 各项的和相等,则称
各项的和相等,则称 和
和 为数列
为数列 的一对“完美互补子列”.
的一对“完美互补子列”.(1)若数列
 为
为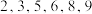 ,请问
,请问 是否存在“完美互补子列”?并说明理由;
是否存在“完美互补子列”?并说明理由;(2)已知共100项的等比数列
 为递减数列,且
为递减数列,且 ,公比为q.若
,公比为q.若 存在“完美互补子列”,求证:
存在“完美互补子列”,求证: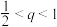 ;
;(3)数列
 满足
满足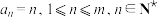 .设
.设 共有
共有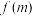 对“完美互补子列”,求证:当
对“完美互补子列”,求证:当 和
和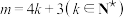 时,
时, 都存在“完美互补子列”且
都存在“完美互补子列”且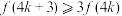 .
.
您最近一年使用:0次



