名校
1 . 在正四棱柱 中,
中,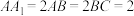 ,
, 是棱
是棱 上的中点.
上的中点. ;
;
(2)异面直线 与
与 所成角的余弦值.
所成角的余弦值.
 中,
中,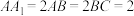 ,
, 是棱
是棱 上的中点.
上的中点.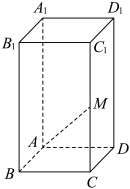
 ;
;(2)异面直线
 与
与 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2023-10-20更新
|
4238次组卷
|
17卷引用:福建省仙游县枫亭中学2022-2023学年高二下学期期中考试数学试题
福建省仙游县枫亭中学2022-2023学年高二下学期期中考试数学试题北京市丰台区2022-2023学年高二上学期数学期末练习数学试题四川省雅安市雅安中学2022-2023学年高二下学期期中数学(理)试题第一章 空间向量与立体几何 (单元测)河南省郑州市基石中学2022-2023学年高二下学期期中数学试题江苏省南通市如皋中学2024届高三创新实验班夏令营数学试题(已下线)第三章 空间向量与立体几何(基础巩固检测卷)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)北京市朝阳区东北师范大学附属中学朝阳学校2023-2024学年高二上学期第一次学习质量监测与反馈数学试题湖南省长沙市德成学校2023-2024学年高二上学期10月月考数学试题海南省川绵中学2023-2024学年高二上学期10月第一次月考数学试题山西省运城市景胜中学2023-2024学年高二上学期10月月考数学试题(A卷)广东省佛山市顺德德胜学校2023-2024学年高二上学期期中数学试题广西壮族自治区桂林市灵川县广西师大附中2023-2024学年高二上学期段考(期中)数学试题河南省三门峡市渑池县第二高级中学2023-2024学年高二上学期第二次月考(11月)数学试题湖南省张家界市民族中学2023-2024学年高二上学期第二次月考数学试题(已下线)考点12 空间角 2024届高考数学考点总动员 【讲】四川省绵阳市盐亭中学2024-2025学年高二上学期10月月考数学试题
名校
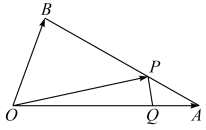
2 . 如图,在 中,
中, 为
为 边上一点,且
边上一点,且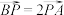 .
.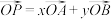 ,求实数
,求实数 、
、 的值;
的值;
(2)若 ,求
,求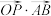 的值;
的值;
(3)设点 满足
满足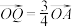 ,求证:
,求证: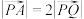 .
.
 中,
中, 为
为 边上一点,且
边上一点,且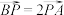 .
.
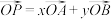 ,求实数
,求实数 、
、 的值;
的值;(2)若
 ,求
,求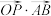 的值;
的值;(3)设点
 满足
满足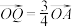 ,求证:
,求证: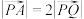 .
.
您最近一年使用:0次
2022-12-09更新
|
2163次组卷
|
11卷引用:福建省宁德市福安市阳光国际集团福建区域联考2022-2023学年高一下学期期中数学试题
福建省宁德市福安市阳光国际集团福建区域联考2022-2023学年高一下学期期中数学试题第9章《平面向量》单元达标高分突破必刷卷(基础版)第八章 向量的数量积与三角恒等变换(A卷·基础通关练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教B版2019必修第三册)第六章 平面向量及其应用(A卷·基础提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第二册)(已下线)专题6.14 平面向量及其应用全章综合测试卷(基础篇)-2022-2023学年高一数学举一反三系列(人教A版2019必修第二册)江苏省盐城市东台创新高级中学2022-2023学年高一下学期2月月检测数学试题上海市曹杨第二中学2021-2022学年高一下学期期末数学试题广东省深圳市龙华外国语高级中学2023-2024学年高一下学期第一次段考数学试卷单元测试A卷——第六章?平面向量及其应用(已下线)上海市高一下学期期末真题必刷03-期末考点大串讲(沪教版2020必修二)辽宁省大连市滨城高中联盟2023-2024学年高一下学期5月期中考试数学试题
名校
解题方法
3 . 如图,在正方体 中,
中, 是
是 的中点,
的中点,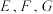 分别是
分别是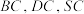 的中点,求证:
的中点,求证: 平面
平面 ;
;
(2)平面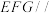 平面
平面 .
.
 中,
中, 是
是 的中点,
的中点,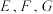 分别是
分别是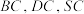 的中点,求证:
的中点,求证:
 平面
平面 ;
;(2)平面
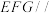 平面
平面 .
.
您最近一年使用:0次
2022-11-16更新
|
6901次组卷
|
81卷引用:福建省仙游县枫亭中学2022-2023学年高一下学期期中考试数学试题
福建省仙游县枫亭中学2022-2023学年高一下学期期中考试数学试题福建省南平市建瓯市芝华中学2019-2020学年高一上学期期中(B)卷数学试题福建省莆田锦江中学2020-2021学年高一下学期期中考试数学试题(已下线)8.5.3平面与平面平行(已下线)第八章立体几何初步(基础检测卷)(已下线)8.5 空间直线、平面的平行(精练)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)8.5.3 平面与平面平行 (精讲)(1)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)8.5.3 平面与平面平行(分层作业)-【上好课】2022-2023学年高一数学同步备课系列(人教A版2019必修第二册)(已下线)专题训练:线线、线面、面面平行证明第八章 立体几何初步(B卷·能力提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第二册)(已下线)专题8.9 空间直线、平面的平行(重难点题型精讲)-2022-2023学年高一数学举一反三系列(人教A版2019必修第二册)(已下线)模块三 专题8(立体几何初步)拔高能力练(北师大版)(已下线)模块三 专题7 大题分类练(立体几何初步)拔高能力练(人教A)广西百色市2022-2023学年高一下学期数学期末考试模拟试题(已下线)模块三 专题8大题分类练(立体几何初步)拔高能力练(苏教版)(已下线)期末专题09 立体几何大题综合-【备战期末必刷真题】广东省深圳市龙岗区德琳学校2022-2023学年高一下学期期中数学试题四川省绵阳市绵阳博美实验高级中学2022-2023学年高一下学期6月月考数学试题(已下线)模块二 专题4 立体几何中的平行与垂直的位置关系 基础卷A(已下线)模块二 专题7 立体几何中的平行与垂直的位置关系 基础卷A新疆阿克苏地区柯坪县柯坪湖州国庆中学2023-2024学年高二上学期9月月考数学试题四川省南充市南部县第二中学2023-2024学年高二上学期10月月考数学试题陕西省西安市2022-2023学年高一下学期期中数学模拟试题(已下线)专题04平面与平面的位置关系(2个知识点8种题型)-【倍速学习法】2023-2024学年高二数学核心知识点与常见题型通关讲解练(沪教版2020必修第三册)2016-2017学年山西怀仁县一中高二理上月考一数学试卷2016-2017学年黑龙江大庆杜蒙县高二上月考一数学试卷河北省沧州市第一中学2016-2017学年高一下学期第二次月考数学试题山东省枣庄市第三中学2017-2018学年高一1月学情调查数学试题山东省武城县第二中学高中数学必修二人教A版第二章 直线与平面、平面与平面平行的练习题2018-2019学年高中数学必修2人教版:模块综合评价【全国百强校】青海省西宁市第四高级中学2018-2019学年高二上学期第一次月考数学试题(已下线)专题8.4 直线、平面平行的判定及其性质(讲)-浙江版《2020年高考一轮复习讲练测》人教A版(2019) 必修第二册 过关斩将 第八章 8.5. 空间直线、平面的平行 8.5.3 平面与平面平行人教B版(2019) 必修第四册 过关斩将 第十一章 立体几何初步 11.3.3 平面与平面平行2020届宁夏银川市宁大附中高三上学期第四次月考数学(文)试题(已下线)【新东方】杭州新东方高二数学试卷253陕西省西安市高新一中2019-2020学年高二下学期第二次月考数学(理)试题(已下线)专题12 空间直线、平面的平行(核心素养练习)-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第二册)-《高中新教材知识讲学》山东省临沂第一中学2019-2020学年高一下学期期中考试数学试题河北省鸡泽县第一中学2019-2020学年高一下学期开学考试数学试题山东省潍坊一中2019-2020学年高一下学期期中考试数学试题河北省邢台八中2019-2020学年高二上学期期中数学试题吉林省梅河口市第五中学2019-2020学年高一6月月考数学试题(已下线)专题20+立体几何综合-2020年高考数学(文)母题题源解密(全国Ⅱ专版)(已下线)【新教材精创】11.3.3 平面与平面平行(第2课时)导学案(1)贵州省兴仁市凤凰中学2018-2019学年高一下学期第四次月考(期末)数学试题甘肃省兰州市东方中学2020-2021学年第一学期高二年级期中文科考试试题山西省运城市高中联合体2020-2021学年高二上学期期中数学试题(已下线)专题8.4 直线、平面平行的判定及性质(讲)-2021年新高考数学一轮复习讲练测(已下线)专题8.4 直线、平面平行的判定及性质(精讲)-2021年高考数学(理)一轮复习学与练(已下线)山东省济南大学城实验高中2019-2020学年高一下学期期中数学试题(已下线)8.4 空间直线、平面的平行--2020--2021高中数学新教材配套提升训练(人教A版必修第二册)(已下线)专题8.4 空间直线、平面的平行(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)安徽省六安市城南中学2020-2021学年高二(卓越、宏志班)上学期期中数学(理)试题(已下线)专题11.2平面与空间中的平行关系(B卷提升篇)-2020-2021学年高一数学必修第四册同步单元AB卷(新教材人教B版)河北省保定市博野县实验中学2020-2021学年高一下学期期中数学试题(已下线)专题34直线、平面平行的判定与性质-2022年(新高考)数学高频考点+重点题型贵州省兴仁市凤凰中学2020-2021学年高一下学期第四次月考数学试题(已下线)考点31 直线、平面平行的判定及其性质-备战2022年高考数学一轮复习考点帮(浙江专用)北师大版 必修2 过关斩将 第一章 立体几何初步 §5 平行关系 5.1 平行关系的判定(已下线)专题8.4 直线、平面平行的判定及性质(讲)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)第35讲 直线、平面平行的判定及性质 (讲) — 2022年高考数学一轮复习讲练测(课标全国版)四川省眉山市仁寿县四校联考2021-2022学年高二上学期期中数学试题(已下线)第10课时 课后 空间中平面与平面的平行(已下线)8.5 空间直线、平面的平行(精练)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第二册)陕西省渭南市咸林中学2021-2022学年高一上学期第三阶段质量检测数学试题(已下线)8.5.3平面与平面平行(练案)-2021-2022学年高一数学同步备课 (人教A版2019 必修第二册)安徽省宣城中学2021-2022学年高一下学期期中数学试题陕西省咸阳市高新一中2022-2023学年高二上学期期中文科数学试题青海省海南藏族自治州高级中学2022-2023学年高二上学期10月月考数学试题河南省周口市太康县第一高级中学2021-2022学年高一下学期4月月考数学试题安徽省滁州市定远县育才学校2021-2022学年高一下学期5月月考数学试题安徽省滁州市定远县育才学校2021-2022学年高一下学期期末考试数学试题河北省唐山英才国际学校2022-2023学年中韩高二上学期11月月考数学试题(已下线)专题20 立体几何综合-2020年高考数学(文)母题题源解密(全国Ⅱ专版)(已下线)第10讲空间直线、平面的平行(核心考点讲与练)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)(原卷版)(已下线)第八章立体几何8.3 平行关系(已下线)8.5.3 平面与平面平行【第一练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)第8.5.3讲 平面与平面平行-同步精讲精练宝典(人教A版2019必修第二册)四川省南充市西充中学校2023-2024学年高一下学期5月月考数学试题陕西省西安市临潼区临潼中学2023-2024学年高一下学期期中质量检测数学试题
名校
解题方法
4 . 已知函数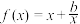 过点
过点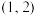 .
.
(1)判断 在区间
在区间 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)求函数 在
在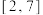 上的最大值和最小值.
上的最大值和最小值.
 过点
过点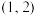 .
.(1)判断
 在区间
在区间 上的单调性,并用定义证明;
上的单调性,并用定义证明;(2)求函数
 在
在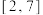 上的最大值和最小值.
上的最大值和最小值.
您最近一年使用:0次
2023-10-12更新
|
3506次组卷
|
6卷引用:福建省厦门市第六中学2023-2024学年高一上学期期中考试数学试题
名校
解题方法
5 . 如图,在棱长为2的正方体 中,
中, 为
为 的中点,
的中点, 为
为 的中点.
的中点.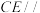 平面
平面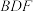 ;
;
(2)求三棱锥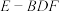 的体积.
的体积.
 中,
中, 为
为 的中点,
的中点, 为
为 的中点.
的中点.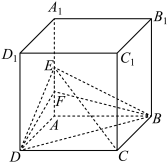
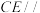 平面
平面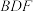 ;
;(2)求三棱锥
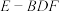 的体积.
的体积.
您最近一年使用:0次
2022-12-03更新
|
5458次组卷
|
11卷引用:福建福州延安中学2022-2023学年高二下学期第一次数学会考模拟试题
福建福州延安中学2022-2023学年高二下学期第一次数学会考模拟试题贵州省黔西南布依族苗族自治州2022-2023学年高二上学期期末教学质量监测数学试题(已下线)8.5.1-8.5.2直线与直线平行、直线与平面平行(已下线)8.5.2直线与平面平行(精练)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)广东省湛江市第二十一中学2022-2023学年高一下学期期中数学试题湖南省长沙市长郡中学2022-2023学年高一下学期期末数学试题山东省济宁市曲阜孔子高级中学2022-2023学年高一下学期6月月考数学试题(已下线)第8章立体几何初步(基础、典型、易错、压轴)分类专项训练新疆阿克苏市第三高级中学2023-2024学年高二上学期第一次月考数学试题黑龙江哈尔滨市第九中学校2021—2022年高一下学期期中数学试题贵州省遵义市桐梓县荣兴高级中学2023-2024学年高二下学期第一次(3月)月考数学试题
名校
6 . 如图,三棱锥 中的三条棱
中的三条棱 两两互相垂直,
两两互相垂直,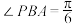 ,点
,点 满足
满足 .
.
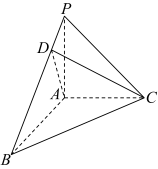
(1)证明: 平面
平面 .
.
(2)若 ,求异面直线
,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
 中的三条棱
中的三条棱 两两互相垂直,
两两互相垂直,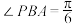 ,点
,点 满足
满足 .
.
(1)证明:
 平面
平面 .
.(2)若
 ,求异面直线
,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2023-10-10更新
|
2098次组卷
|
3卷引用:福建省莆田第五中学2023-2024学年高二上学期期中考试数学试题
名校
7 . 求证: 是一元二次方程
是一元二次方程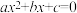 的一个根的充要条件是
的一个根的充要条件是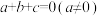 .
.
 是一元二次方程
是一元二次方程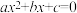 的一个根的充要条件是
的一个根的充要条件是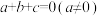 .
.
您最近一年使用:0次
2022-10-23更新
|
847次组卷
|
7卷引用:福建省霞浦第一中学2022-2023学年高一上学期期末线上质量检测数学试题
福建省霞浦第一中学2022-2023学年高一上学期期末线上质量检测数学试题(已下线)1.4 充分必要条件(精讲)-《一隅三反》(已下线)2.1必要条件与充分条件-高一数学同步精品课堂(北师大版2019必修第一册)贵州省贵阳市“三新”改革联盟校2022-2023学年高一上学期联考试题(二)数学试题陕西省西安市高新第七高级中学(长安区第七中学)2022-2023学年高二上学期第二次月考数学试题(已下线)1.4.2 充要条件——课后作业(巩固版)广东省华侨中学2024-2025学年高一上学期10月月考数学试题
名校
8 . 17世纪,法国数学家马林·梅森在欧几里得、费马等人研究的基础上,对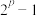 (
( 为素数)型的数作了大量的研算,他在著作《物理数学随感》中断言:在
为素数)型的数作了大量的研算,他在著作《物理数学随感》中断言:在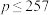 的素数中,当
的素数中,当 ,3,5,7,13,17,19,31,67,127,257时,
,3,5,7,13,17,19,31,67,127,257时,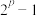 是素数,其它都是合数.除了
是素数,其它都是合数.除了 和
和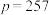 两个数被后人证明不是素数外,其余都已被证实.人们为了纪念梅森在
两个数被后人证明不是素数外,其余都已被证实.人们为了纪念梅森在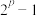 型素数研究中所做的开创性工作,就把
型素数研究中所做的开创性工作,就把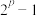 型的素数称为“梅森素数”,记为
型的素数称为“梅森素数”,记为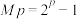 .几个年来,人类仅发现51个梅森素数,由于这种素数珍奇而迷人,因此被人们答为“数海明珠”.已知第7个梅森素数
.几个年来,人类仅发现51个梅森素数,由于这种素数珍奇而迷人,因此被人们答为“数海明珠”.已知第7个梅森素数 ,第8个梅森素数
,第8个梅森素数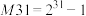 ,则
,则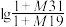 约等于(参考数据:
约等于(参考数据: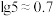 )( )
)( )
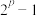 (
( 为素数)型的数作了大量的研算,他在著作《物理数学随感》中断言:在
为素数)型的数作了大量的研算,他在著作《物理数学随感》中断言:在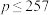 的素数中,当
的素数中,当 ,3,5,7,13,17,19,31,67,127,257时,
,3,5,7,13,17,19,31,67,127,257时,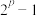 是素数,其它都是合数.除了
是素数,其它都是合数.除了 和
和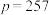 两个数被后人证明不是素数外,其余都已被证实.人们为了纪念梅森在
两个数被后人证明不是素数外,其余都已被证实.人们为了纪念梅森在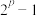 型素数研究中所做的开创性工作,就把
型素数研究中所做的开创性工作,就把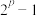 型的素数称为“梅森素数”,记为
型的素数称为“梅森素数”,记为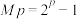 .几个年来,人类仅发现51个梅森素数,由于这种素数珍奇而迷人,因此被人们答为“数海明珠”.已知第7个梅森素数
.几个年来,人类仅发现51个梅森素数,由于这种素数珍奇而迷人,因此被人们答为“数海明珠”.已知第7个梅森素数 ,第8个梅森素数
,第8个梅森素数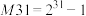 ,则
,则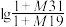 约等于(参考数据:
约等于(参考数据: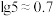 )( )
)( )| A.17.1 | B.8.4 | C.6.6 | D.3.6 |
您最近一年使用:0次
2023-08-11更新
|
1077次组卷
|
5卷引用:福建省三明市2023届高三三模数学试题
福建省三明市2023届高三三模数学试题(已下线)专题4.3 对数【七大题型】-举一反三系列(已下线)4.3 对数运算(精讲)-《一隅三反》浙江省杭州绿城育华学校2023-2024学年高一上学期期末考试数学试题(已下线)专题21 指数、对数、幂函数小题
名校
9 . 已知函数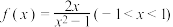 .
.
(1)判断函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)判断函数 的单调性并证明.
的单调性并证明.
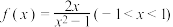 .
.(1)判断函数
 的奇偶性,并说明理由;
的奇偶性,并说明理由;(2)判断函数
 的单调性并证明.
的单调性并证明.
您最近一年使用:0次
2023-02-21更新
|
1635次组卷
|
2卷引用:福建省厦门双十中学2023-2024学年高一上学期期中考试数学试题
10 . 已知幂函数 的图象过点
的图象过点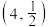 .
.
(1)求此函数的解析式;
(2)根据单调性的定义判断函数 在
在 上的单调性;
上的单调性;
(3)判断函数 的奇偶性,并加以证明.
的奇偶性,并加以证明.
 的图象过点
的图象过点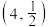 .
.(1)求此函数的解析式;
(2)根据单调性的定义判断函数
 在
在 上的单调性;
上的单调性;(3)判断函数
 的奇偶性,并加以证明.
的奇偶性,并加以证明.
您最近一年使用:0次
2023-03-13更新
|
1677次组卷
|
5卷引用:福建省莆田第十五中学2022-2023学年高二下学期第一次月考(3月)数学试题
福建省莆田第十五中学2022-2023学年高二下学期第一次月考(3月)数学试题河北省衡水市第十三中学2022-2023学年高一下学期开学考试数学试题(已下线)第四章 幂函数、指数函数与对数函数(单元重点综合测试)-速记·巧练(沪教版2020必修第一册)(已下线)5.2.2 函数的单调性-数学同步精品课堂(沪教版2020必修第一册)贵州省安顺市镇宁实验学校2023-2024学年高一上学期期中数学试题



