解题方法
1 . 已知正四面体 的四个面分别标注有字母
的四个面分别标注有字母 ,随机抛掷该四面体,各面接触桌面的概率均相等.
,随机抛掷该四面体,各面接触桌面的概率均相等.
(1)若每次抛掷时标注有 的面接触桌面为抛掷成功,将试验进行到恰好出现3次成功时结束试验,求结束试验时所抛掷的次数为4次的概率;
的面接触桌面为抛掷成功,将试验进行到恰好出现3次成功时结束试验,求结束试验时所抛掷的次数为4次的概率;
(2)若每次抛掷标注有 或
或 的面接触桌面为抛掷成功,且试验进行到恰好出现2次成功时结束试验,用
的面接触桌面为抛掷成功,且试验进行到恰好出现2次成功时结束试验,用 表示抛掷次数.
表示抛掷次数.
①求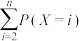 ;
;
②要使得在 次内(含
次内(含 次)结束试验的概率不小于
次)结束试验的概率不小于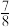 ,求
,求 的最小值.
的最小值.
 的四个面分别标注有字母
的四个面分别标注有字母 ,随机抛掷该四面体,各面接触桌面的概率均相等.
,随机抛掷该四面体,各面接触桌面的概率均相等.(1)若每次抛掷时标注有
 的面接触桌面为抛掷成功,将试验进行到恰好出现3次成功时结束试验,求结束试验时所抛掷的次数为4次的概率;
的面接触桌面为抛掷成功,将试验进行到恰好出现3次成功时结束试验,求结束试验时所抛掷的次数为4次的概率;(2)若每次抛掷标注有
 或
或 的面接触桌面为抛掷成功,且试验进行到恰好出现2次成功时结束试验,用
的面接触桌面为抛掷成功,且试验进行到恰好出现2次成功时结束试验,用 表示抛掷次数.
表示抛掷次数.①求
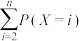 ;
;②要使得在
 次内(含
次内(含 次)结束试验的概率不小于
次)结束试验的概率不小于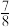 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
2 . 已知抛物线 的焦点为F,该抛物线C与直线
的焦点为F,该抛物线C与直线 :
: 相交于M,N两点,则
相交于M,N两点,则 的最小值为( )
的最小值为( )
 的焦点为F,该抛物线C与直线
的焦点为F,该抛物线C与直线 :
: 相交于M,N两点,则
相交于M,N两点,则 的最小值为( )
的最小值为( )A.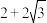 | B.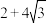 |
C.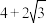 | D. |
您最近一年使用:0次
2024-08-14更新
|
480次组卷
|
4卷引用:安徽省皖北县中联盟(省重点高中)2023-2024学年高二下学期期中数学试题
安徽省皖北县中联盟(省重点高中)2023-2024学年高二下学期期中数学试题河北省邯郸市武安市第一中学2024-2025学年高二上学期10月期中考试数学试题(已下线)重组4高二期中真题重组卷(浙江卷)A基础卷(已下线)专题9 抛物线中的轨迹、最值、光学性质等问题【练】(高二期中压轴专项)
3 . 已知椭圆 的离心率为
的离心率为 ,点
,点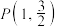 在
在 上.
上.
(1)求椭圆 的方程;
的方程;
(2)若直线 与
与 相交于
相交于 两点,
两点, 中点
中点 在曲线
在曲线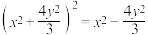 上,探究直线
上,探究直线 与双曲线
与双曲线 的位置关系.
的位置关系.
 的离心率为
的离心率为 ,点
,点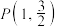 在
在 上.
上.(1)求椭圆
 的方程;
的方程;(2)若直线
 与
与 相交于
相交于 两点,
两点, 中点
中点 在曲线
在曲线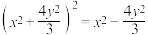 上,探究直线
上,探究直线 与双曲线
与双曲线 的位置关系.
的位置关系.
您最近一年使用:0次
4 . 已知函数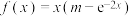 ,曲线
,曲线 上存在不同的两点,使得曲线在这两点处的切线都与直线
上存在不同的两点,使得曲线在这两点处的切线都与直线 平行,则实数
平行,则实数 的取值范围是( )
的取值范围是( )
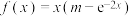 ,曲线
,曲线 上存在不同的两点,使得曲线在这两点处的切线都与直线
上存在不同的两点,使得曲线在这两点处的切线都与直线 平行,则实数
平行,则实数 的取值范围是( )
的取值范围是( )A.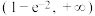 | B. | C. | D.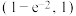 |
您最近一年使用:0次
解题方法
5 . 如图是一个装有水的全封闭直三棱柱容器 ,
,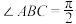 ,
,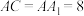 ,若水的体积恰好是该容器体积的一半,容器厚度忽略不计,则( )
,若水的体积恰好是该容器体积的一半,容器厚度忽略不计,则( )
 ,
,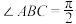 ,
,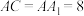 ,若水的体积恰好是该容器体积的一半,容器厚度忽略不计,则( )
,若水的体积恰好是该容器体积的一半,容器厚度忽略不计,则( )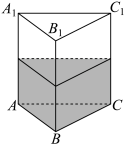
A.当底面 水平放置后,将容器绕着 水平放置后,将容器绕着 转动(转动过程中 转动(转动过程中 始终保持水平),有水的部分是棱柱 始终保持水平),有水的部分是棱柱 |
B.转动容器,当平面 水平放置时,容器内水面形成的截面为DEFG,则D,E,F,G都是所在棱的中点 水平放置时,容器内水面形成的截面为DEFG,则D,E,F,G都是所在棱的中点 |
C.容器中水的体积与直三棱柱外接球体积之比至多为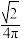 |
| D.在翻滚转动容器的过程中,有水的部分不可能是三棱锥 |
您最近一年使用:0次
6 . 设 的内角A,B,C的对边分别为a,b,c,且满足
的内角A,B,C的对边分别为a,b,c,且满足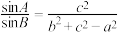 .
.
(1)若 ,
,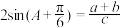 ,求
,求 的面积;
的面积;
(2)若 是锐角三角形,
是锐角三角形,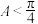 ,求
,求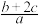 的取值范围.
的取值范围.
 的内角A,B,C的对边分别为a,b,c,且满足
的内角A,B,C的对边分别为a,b,c,且满足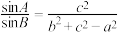 .
.(1)若
 ,
,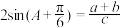 ,求
,求 的面积;
的面积;(2)若
 是锐角三角形,
是锐角三角形,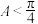 ,求
,求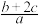 的取值范围.
的取值范围.
您最近一年使用:0次
7 . 设抛物线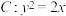 ,点
,点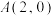 ,
, ,过点A的直线l与C交于M,N两点.
,过点A的直线l与C交于M,N两点.
(1)当l与x轴垂直时,求直线 的方程;
的方程;
(2)证明: .
.
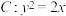 ,点
,点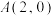 ,
, ,过点A的直线l与C交于M,N两点.
,过点A的直线l与C交于M,N两点.(1)当l与x轴垂直时,求直线
 的方程;
的方程;(2)证明:
 .
.
您最近一年使用:0次
名校
8 . 如图,在底面为平行四边形的直四棱柱 中,
中,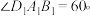 ,
, ,
, 、
、 分别为棱
分别为棱 、
、 的中点,则( )
的中点,则( )
 中,
中,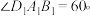 ,
, ,
, 、
、 分别为棱
分别为棱 、
、 的中点,则( )
的中点,则( )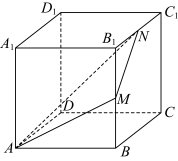
A.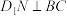 |
B. 与平面 与平面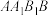 所成角的余弦值为 所成角的余弦值为 |
C.三棱柱 的外接球的表面积为 的外接球的表面积为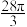 |
D.点 到平面 到平面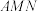 的距离为 的距离为 |
您最近一年使用:0次
2024-06-26更新
|
251次组卷
|
2卷引用:安徽省亳州市第一中学2023-2024学年高一下学期期中检测数学A卷
名校
解题方法
9 . 平面向量是数学中一个非常重要的概念,它具有广泛的工具性,平面向量的引入与运用,大大拓展了数学分析和几何学的领域,使得许多问题的求解和理解更加简单和直观,在实际应用中,平面向量在工程、物理学、计算机图形等各个领域都有广泛的应用,平面向量可以方便地描述几何问题,进行代数运算,描述几何变换,表述物体的运动和速度等,因此熟练掌握平面向量的性质与运用,对于提高数学和物理学的理解和能力,具有非常重要的意义,平面向量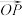 的大小可以由模来刻画,其方向可以由以
的大小可以由模来刻画,其方向可以由以 轴的非负半轴为始边,
轴的非负半轴为始边,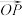 所在射线为终边的角
所在射线为终边的角 来刻画.设
来刻画.设 ,则
,则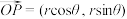 .另外,将向量
.另外,将向量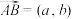 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 角后得到向量
角后得到向量 .如果将
.如果将 的坐标写成
的坐标写成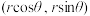 (其中
(其中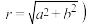 ,那么
,那么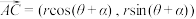 .根据以上材料,回答下面问题:
.根据以上材料,回答下面问题: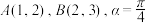 ,求向量
,求向量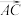 的坐标;
的坐标;
(2)用向量法证明余弦定理;
(3)如图,点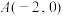 和
和 分别为等腰直角
分别为等腰直角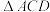 和等腰直角
和等腰直角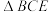 的直角顶点,连接DE,求DE的中点坐标.
的直角顶点,连接DE,求DE的中点坐标.
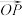 的大小可以由模来刻画,其方向可以由以
的大小可以由模来刻画,其方向可以由以 轴的非负半轴为始边,
轴的非负半轴为始边,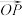 所在射线为终边的角
所在射线为终边的角 来刻画.设
来刻画.设 ,则
,则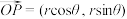 .另外,将向量
.另外,将向量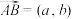 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 角后得到向量
角后得到向量 .如果将
.如果将 的坐标写成
的坐标写成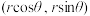 (其中
(其中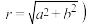 ,那么
,那么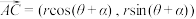 .根据以上材料,回答下面问题:
.根据以上材料,回答下面问题: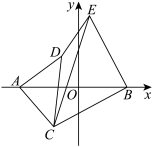
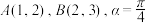 ,求向量
,求向量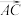 的坐标;
的坐标;(2)用向量法证明余弦定理;
(3)如图,点
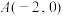 和
和 分别为等腰直角
分别为等腰直角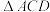 和等腰直角
和等腰直角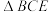 的直角顶点,连接DE,求DE的中点坐标.
的直角顶点,连接DE,求DE的中点坐标.
您最近一年使用:0次
名校
解题方法
10 . 已知数列 的前
的前 项和
项和 满足
满足 ,记
,记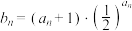 ,数列
,数列 的前
的前 项和为
项和为 ,且对任意的
,且对任意的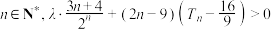 恒成立,则( )
恒成立,则( )
 的前
的前 项和
项和 满足
满足 ,记
,记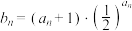 ,数列
,数列 的前
的前 项和为
项和为 ,且对任意的
,且对任意的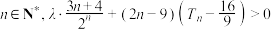 恒成立,则( )
恒成立,则( )A.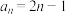 | B.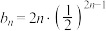 |
C.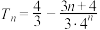 | D. 的取值范围是 的取值范围是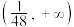 |
您最近一年使用:0次
2024-06-18更新
|
258次组卷
|
2卷引用:安徽省亳州市涡阳县2023-2024学年高二下学期5月期中考试数学试题



